Cosecant (csc) is a mathematical function that is often used in trigonometry. It is defined as the reciprocal of the sine function. In other words, if we have a right-angled triangle with one of its angles equal to θ, and the length of the side opposite to θ is a, and the length of the hypotenuse is h, then the cosecant of θ is defined as h/a.
The cosecant function is used to find the angle whose sine value is equal to a givn ratio of the opposite side and hypotenuse. For example, if we know that the sine of an angle is 1/2, we can use the cosecant function to find the value of the angle. The cosecant of an angle whose sine is 1/2 is 2, so the angle is equal to the inverse cosecant of 2, or csc-1(2).
It is important to note that the cosecant function is not the same as the inverse of the sine function. The inverse of the sine function is denoted as sin-1 or arcsin, and it is used to find the angle whose sine value is equal to a given ratio of the opposite side and hypotenuse. The inverse cosecant function, on the other hand, is denoted as csc-1 or arccsc, and it is used to find the angle whose cosecant value is equal to a given ratio of the hypotenuse and opposite side.
The cosecant function is defined as the reciprocal of the sine function and is used to find the angle whose sine value is equal to a given ratio of the opposite side and hypotenuse. However, it is not the same as the inverse of the sine function, which is used to find the angle whose sine value is equal to a given ratio of the opposite side and hypotenuse.
Are Cosecant and Inverse Sine the Same?
Cosecant and inverse of sine are not the same. They are two different mathematical concepts.
Cosecant (csc) is a trigonometric function that represents the reciprocal of the sine function (sin). It is defined as the ratio of the hypotenuse to the opposite side in a right-angled triangle. In other words, csc θ = 1/sin θ, where θ is the angle measure in radians.
On the other hand, the inverse of a function is a mathematical operation that reverses the effect of the original function. Inverse functions are denoted by adding a “-1” superscript to the function symbol. For example, the inverse of sine is denoted as sin-1.
Therefore, the inverse of sine (sin-1) and cosecant (csc) are not the same. While the inverse of sine represents the angle wose sine is a given value, cosecant represents the reciprocal of the sine function.
Cosecant and inverse of sine are two distinct mathematical concepts that have different definitions and applications.
Source: math.libretexts.org
The Inverse of Sin: An Overview
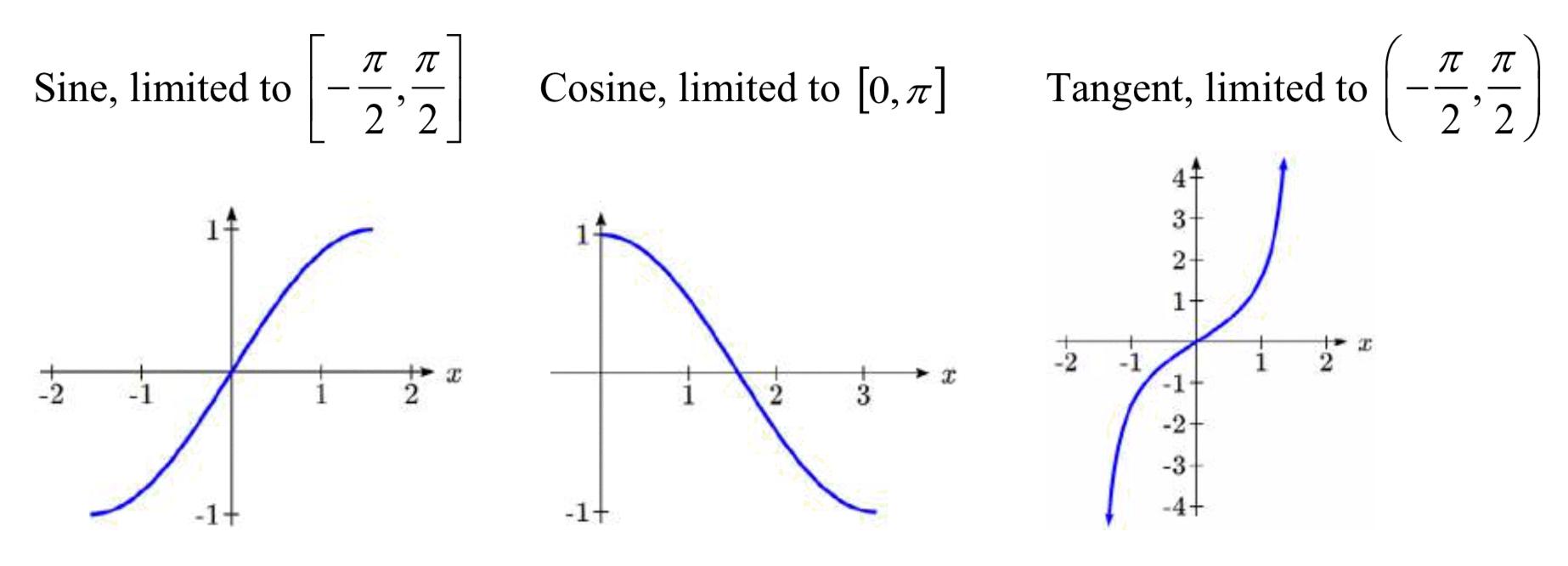
The inverse of sine is kown as the arcsine function. It is also referred to as the inverse sine or the sin^-1 function. The arcsine function is the inverse of the sine function, which means that it allows us to find the angle whose sine is equal to a given ratio of the opposite side to the hypotenuse of a right triangle.
The arcsine function is a one-to-one function, which means that for every value of sine, there is a unique value of arcsine. The range of the arcsine function is between -π/2 and π/2 radians or between -90° and 90° in degrees.
The notation for the arcsine function is sin^-1(x), where x is the ratio of the opposite side to the hypotenuse. For example, if sinθ = 0.5, then θ = sin^-1(0.5) = 30°.
It is important to note that the arcsine function is only defined for values of x between -1 and 1. Any value outside of this range will result in an error.
Here are some key points to remember about the arcsine function:
– It is the inverse of the sine function.
– It allows us to find the angle whose sine is equal to a given ratio of the opposite side to the hypotenuse.
– The range of the arcsine function is between -π/2 and π/2 radians or between -90° and 90° in degrees.
– The notation for the arcsine function is sin^-1(x), where x is the ratio of the opposite side to the hypotenuse.
– The arcsine function is only defined for values of x between -1 and 1.
What is the Inverse of CSC?
Cosecant (csc) is a reciprocal function in trigonometry, which is the inverse of the sine function (sin). It is calculated as the ratio of the length of the hypotenuse of a right triangle to the length of its opposite side. In other words, it is the reciprocal of the sine function, which means that the vlue of the cosecant of an angle is equal to the reciprocal of the sine of that angle. The formula for calculating the cosecant of an angle is:
Cscθ = 1/sinθ
Where θ is the angle in radians or degrees. In trigonometry, the cosecant function is denoted by the abbreviation “csc”. It is one of the six trigonometric functions used to calculate the relationship between the sides and angles of a right triangle.
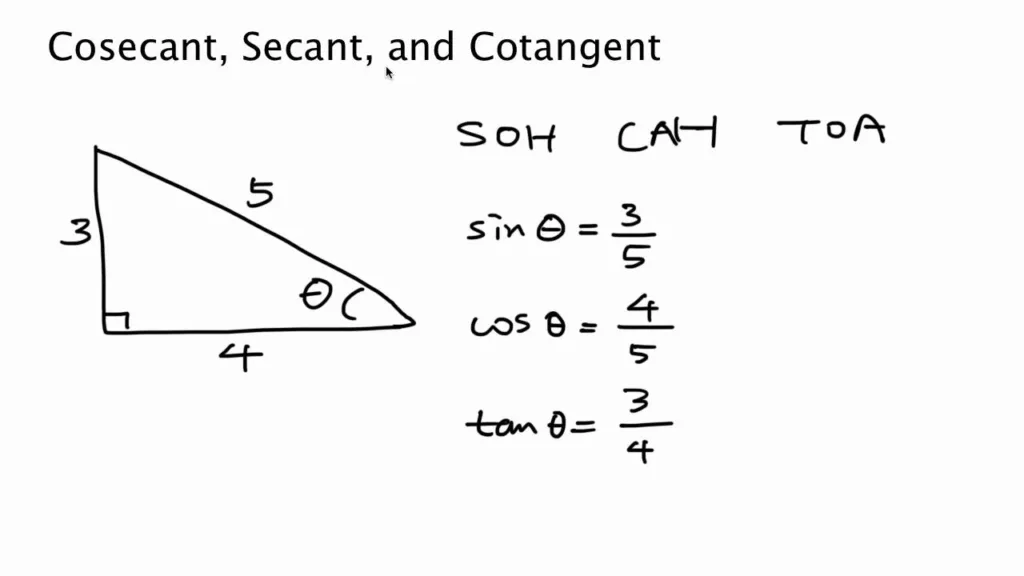
Conclusion
Cosecant (csc) is an important mathematical function that is widely used in trigonometry. It is the reciprocal of the sine (sin) function and can be used to evaluate the angle whose sine value is equal to the ratio of its opposite side and hypotenuse. Cosecant is also one of the three reciprocal functions, the others being secant and cotangent. By understanding the properties and applications of cosecant, students and professionals in various fields can enhance their problem-solving abilities and analytical skills. cosecant is a valuable tool that should be studied and utilized in mathematics and beyond.
