Have you ever wondered about the value of cos 180 degrees? Well, let’s dive into the world of trigonometry and explore the exact value and significance of this intriguing mathematical concept.
To begin with, let’s refresh our memory on what cosine is. Cosine, often abbreviated as cos, is a trigonometric function that helps us determine the ratio of the adjacent side to the hypotenuse in a right-angled triangle. In simpler terms, it allows us to calculate the angle or sides of a triangle when we know the length of one side and the measure of one angle.
When it comes to cos 180 degrees, we are dealing with a unique scenario. As we know, a full circle measures 360 degrees, and 180 degrees is exactly halfway through this circle. So, what does this mean for the value of cosine at this angle?
Well, the value of cos 180 degrees is -1. you read that correctly – negative one! This miht seem a little counterintuitive at first, as we often associate cosine with positive values. However, at 180 degrees, cosine takes on a negative value, indicating a different orientation or direction.
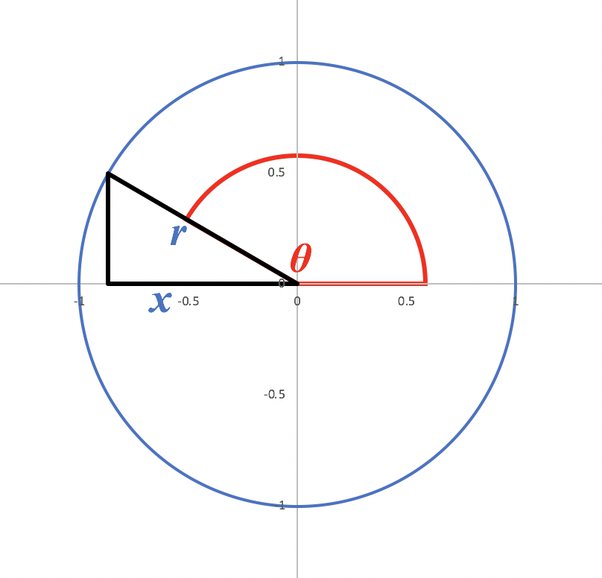
To understand why cos 180 degrees is -1, let’s take a closer look at the unit circle. The unit circle is a circle with a radius of one unit, centered at the origin of a coordinate plane. It is a powerful tool that helps us visualize and understand the trigonometric functions.
At 180 degrees, we find ourselves on the left side of the unit circle, exactly opposite to the point where we started (0 degrees or 360 degrees). Since cosine represents the x-coordinate of a point on the unit circle, we can see that at 180 degrees, the x-coordinate is -1. Hence, cos 180 degrees equals -1.
Now, let’s move on to another trigonometric function closely related to cosine – sine. The sine function, often abbreviated as sin, represents the ratio of the opposite side to the hypotenuse in a right-angled triangle. Its values range from -1 to 1, with zero being a significant point.
At 180 degrees, the exact value of sin is zero. This means that the opposite side of the triangle is zero, indicating that there is no vertical displacement or change in height. In other words, the point lies on the x-axis of the unit circle, where the y-coordinate is zero.
It’s important to note that the relationship between cosine and sine is complementary. This means that if we know the value of cosine at a certain angle, we can determine the value of sine at the complementary angle (90 degrees minus the given angle), and vice versa. In the case of cos 180 degrees being -1, the sine of the complementary angle (90 degrees) is also -1.
Where Is Sin 180 Degrees?
Oh, sin 180 degrees! Let’s dive into the world of trigonometry, my friend. So, sin is short for sine, one of tose fancy trigonometric functions that help us understand angles and sides of right-angled triangles. And when it comes to sin 180 degrees, we’re talking about a specific angle.
Now, picture this: Imagine a circle, a perfect, beautiful circle. It has a center and a circumference, right? Well, if you divide that circle into 360 equal parts, each of those parts is called a degree. So, 180 degrees is essentially half of that circle.
Now, when we talk about sin 180 degrees, we’re asking for the value of the sine function at that specific angle. And guess what? In this case, the sine of 180 degrees is equal to zero! Yup, you heard it right, zero.
To put it in simpler terms, sin 180 degrees tells us that if we have a right-angled triangle with one angle measuring 180 degrees, the ratio of the length of the side opposite that angle to the length of the hypotenuse (the longest side of the triangle) is zero. In other words, the opposite side has no length compared to the hypotenuse.
So, sin 180 degrees takes us to a world where everything is calm, peaceful, and well, zero. It’s like a perfectly still lake without a ripple in sight. The sine function is telling us that at 180 degrees, there’s no height, no upward or downward movement, just a flat line at the x-axis.
Sin 180 degrees is zero. It’s a mathematical fact, and it’s as simple as that. So, next time you come across this little trigonometric gem, you’ll know exactly where to find it – right at the zero mark. Keep on exploring the wonders of trigonometry, my friend!
How Do You Find COS 180 Theta?
To find cos (180° – θ), we need to remember a key identity in trigonometry. The identity states that cos (180° – θ) = – cos θ. Let me explain this in a bit more detail for you:
1. Start with the angle θ.
2. Subtract θ from 180° to get the angle (180° – θ).
3. To find the cosine of (180° – θ), we take the cosine of θ and multiply it by -1.
In simpler terms, the cosine of (180° – θ) is the negative value of the cosine of θ.
For example, let’s say θ is 30°.
– The angle (180° – θ) would be (180° – 30°) = 150°.
– The cosine of 30° is √3/2.
– Using the identity, we find that cos 150° = – cos 30° = -√3/2.
Conclusion
The vale of cos 180 degrees is -1. This means that when we measure an angle of 180 degrees in a right-angled triangle, the cosine of that angle is equal to -1. This result is derived from the properties of trigonometric functions, which help us understand the relationships between angles and sides in triangles.
It is interesting to note that the exact value of sin 180 degrees is zero. This means that when we measure an angle of 180 degrees, the sine of that angle is equal to zero. This can be explained by the fact that the sine function represents the ratio of the length of the side opposite the angle to the length of the hypotenuse in a right-angled triangle. In this case, the side opposite the angle of 180 degrees is zero, resulting in a sine value of zero.
Furthermore, we can also observe some interesting patterns when we consider the complementary angles. For example, the sine of an angle and the cosine of its complementary angle are equal. In the case of 180 degrees, the complementary angle is 0 degrees, and we can see that sin(180 – θ) = sin θ and cos(180 – θ) = -cos θ.
The value of cos 180 degrees is -1, indicating that the cosine of an angle measuring 180 degrees in a right-angled triangle is equal to -1. This result is derived from the properties of trigonometric functions and can be further explored through the relationships between complementary angles.
