Trigonometry can be a confusing topic for many students. One of the most perplexing aspects is understanding the cotangent, or cot, of zero degrees. In this blog post, we’ll demystify what it means and why it’s important to understand in order to tackle trigonometry problems with ease.
The cotangent of an angle is equal to the ratio of the cosine of that angle (cos) to the sine of that angle (sin). This means that if we want to find out what the cot of an angle is, we need to know both its cos and sin values. For example, if an angle has a cosine value of 0.5 and a sine value of 0.866, then its cotangent will be equal to 0.5/0.866=0.578.
Unfortunately, this ratio doesn’t work when it comes to zero degrees because there’s no such thig as a cotangent for zero degrees! This is because when you try to calculate the ratio between cos (0) and sin (0), you get 0/0 which is undefined as it would have a denominator equal to 0. Since tan (0) = 0 and tan is the reciprocal or inverse of cot, this means that cot (0) must also be undefined.
Having said that, understanding why there’s no such thing as a cotangent for zero degrees isn’t just useful for trigonometry problems; it can also help us understand more complex mathematics like calculus and linear algebra too! Knowing how different angles behave in different equations can give us some insight into how those equations work – so even though there’s no such thing as a cotangent for zero degrees, understanding why there isn’t can still help us out in other areas!
Finding the Value of Cot θ
The value of cot θ (also known as the cotangent) when the angle θ is 0° is infinity (∞). This is because the tangent of 0° is 0, and so the cotangent must be equal to 1/0, which is equal to infinity.
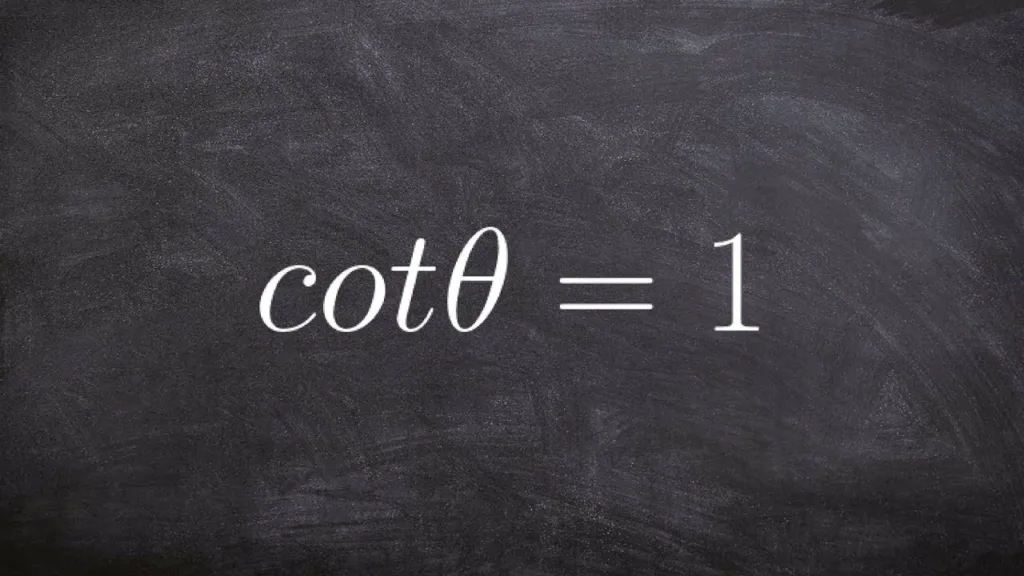
Understanding Why Cot 0 is Undefined
The cotangent of any angle x is the reciprocal of the tangent of that angle. Since the tangent of 0 degrees is 0, the reciprocal would be undefined, as it would have a denominator equal to 0. This means that cot 0 is undefined.
Is Zero Equal to Infinity?
The cotangent of zero degrees (cot 0) is not equal to infinity. The cotangent of an angle is the ratio of the cosine of that angle to the sine of that angle. Since, by definition, the sine and cosine of zero degrees are both equal to zero, then their ratio (cot 0) must also be equal to zero. Infinity is never equal to zero, so it follows that cot 0 can never be equal to infinity.
Does Cot 0 Exist?
No, cot 0 does not exist. The cotangent of a number is the ratio of the length of the opposite side of a right triangle to the length of its adjacent side. When x = 0, both the opposite and adjacent sides are equal in length, which results in a ratio of 1/1. This ratio is undefined, so cot 0 does not exist.
Formula for Cotangent of an Angle
The formula for cot θ is 1/tan θ. In other words, it is the reciprocal of the tangent function. Another way to express cot θ is to use the formula tan(90° – θ). This means that cot θ can be expressed as the tangent of the angle which is 90 degrees minus the given angle θ.
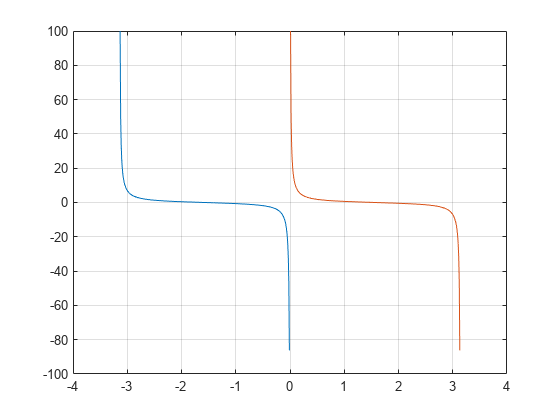
Cot Formula Explained
The cotangent formula is a mathematical expression used to calculate the cotangent of an angle, which is defined as the cosine of that angle divided by the sine of that angle. The formula for calculating the cotangent of an angle x is cot x = cos x sin x . This means that if you know the value of x in degrees, you can use this formula to determine its cotangent value.
Cost of One Item
Cot of 1 is the cotangent of an angle equal to 1 degree. It is a trigonometric function that is used to calculate the ratio between the length of the adjacent side and opposite side of a right triangle. The value of cot 1° is approximately 57.29.
When is Cot θ Undefined?
The cotangent function is undefined when the angle θ has a tangent value of zero. In other words, cot θ is undefined when the angle θ is equal to 0°, ±90°, ±180°, ±270°, etc.
The Value of Cosine When Equal to Zero
The value of cos 0 degrees is 1. This can be illustrated by looking at a unit circle, where the angle 0° is represented by the point (1,0). The cosine of any angle can be calculated by taking the x-coordinate of the point on the unit circle that corresponds to that angle. Since for an angle of 0°, the x-coordinate is 1, it follows that cos 0 = 1. In other words, the cosine of 0 degrees is 1.
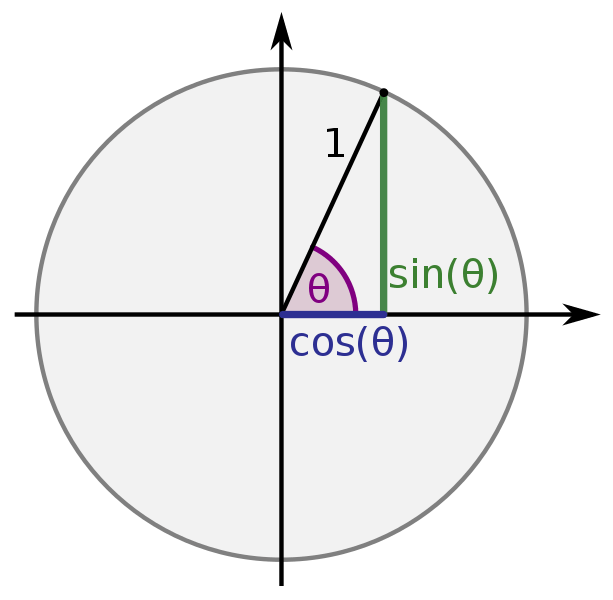
The Significance of Cot 90 Being Equal to Zero
Cot 90 is equal to 0 because the ratio of cos 90 degrees to sin 90 degrees is defined to be zero. This is because the cosine of any angle measured in degrees will always equal 0 when that angle is 90°, while the sine of any angle measured in degrees will always equal 1 when that angle is 90°. Therefore, when you divide 0 by 1, the result will always be 0.
The Cotangent Theorem
The Cot Theorem, also known as the Law of Cotangents, is a trigonometric relationship betwen the lengths of sides of a triangle and the cotangents of the halves of the three angles. It states that the product of two opposite sides of a triangle multiplied by their respective cotangents is equal to the product of the other two sides.
In other words, if we let A, B and C represent the angles in a triangle, and a, b and c represent their corresponding sides, then we can express this relationship as follows:
a*cot(A/2)*b*cot(B/2)=c*cot(C/2)
This theorem is useful in determining missing side lengths when given two side lengths and an angle. It also provides a way to check whether or not a given set of numbers could form a valid triangle.
Conclusion
In conclusion, it can be seen that the cotangent of zero degrees is an undefined value. This is due to the fact that the tangent of zero degrees is zero, which would result in a denominator of zero when calculating the cotangent. Therefore, it is not possible to calculate the cotangent of zero degrees and it must remain an undefined value.
