The cotangent unit circle is a mathematical tool used to calculate angles in a right-angled triangle or other geometric shape. It is based on the concept of cotangent, which is the co-function of tangent. To put it simply, if you know the length of two sides of a right-angled triangle, then you can use the cotangent unit circle to calculate the angle between them.
The cotangent unit circle is made up of two parts: a radius and an arc. The radius is the distance from the center of the circle to any point on its circumference. The arc is a segment of a circumference with its endpoints at two points on the circumference and its midpoint at the center. The arc’s length can be calculated uing trigonometric functions such as sine, cosine, and tangent.
The cotangent formula can be used to calculate an angle from two sides in a right-angled triangle. The formula states that cotθ=cosθsinθ=xy , where θ is the angle corresponding to the point (x, y) on the unit circle and x and y are lengths of sides in the triangle. In other words, if you know two side lengths in a right-angled triangle, then you can use this formula to calculate its angle.
To find cotθ, you need to first plot your point (x, y) on your unit circle graphically or numerically. Then use this data to calculate your angle using trigonometry formulas like sin or cosine. You can also use calculators or computer programs like Geometer’s Sketchpad or Wolfram Alpha to do this for you if needed!
The range of cot–1 is restricted between 0° and 180° or 0 and π radians depending on what type of measurement system you are using for your calculations. For example, if you are calculating angles in degrees then your range will be 0° – 180° while if you are calculating angles in radians then your range will be 0 – π radians instead! This means that when working with larger angles outside this range (such as those greater than 180°), then you may need more than one value for each side length in order to get an accurate reading for your angle calculation.
We hope this guide has been helpful in explaining what exactly a cotangent unit circle is and how it can be used in trigonometry calculations! Feel free to explore more topics related to math by visiting our website or contacting us with any questions that arise as you work through these concepts!
Understanding Cotangent on a Unit Circle
Cotangent on a unit circle is a mathematical concept that allows us to find the cotangent of an angle given the x and y coordinates of a point on the unit circle. To calculate cotangent on a unit circle, we use the formula: cotθ=cosθsinθ=xy which means that given any coordinates (x,y) for a point on the unit circle, we can calculate its angle θ and then use this formula to find its corresponding cotangent. This concept is commonly used in trigonometry and other areas of mathematics such as calculus.
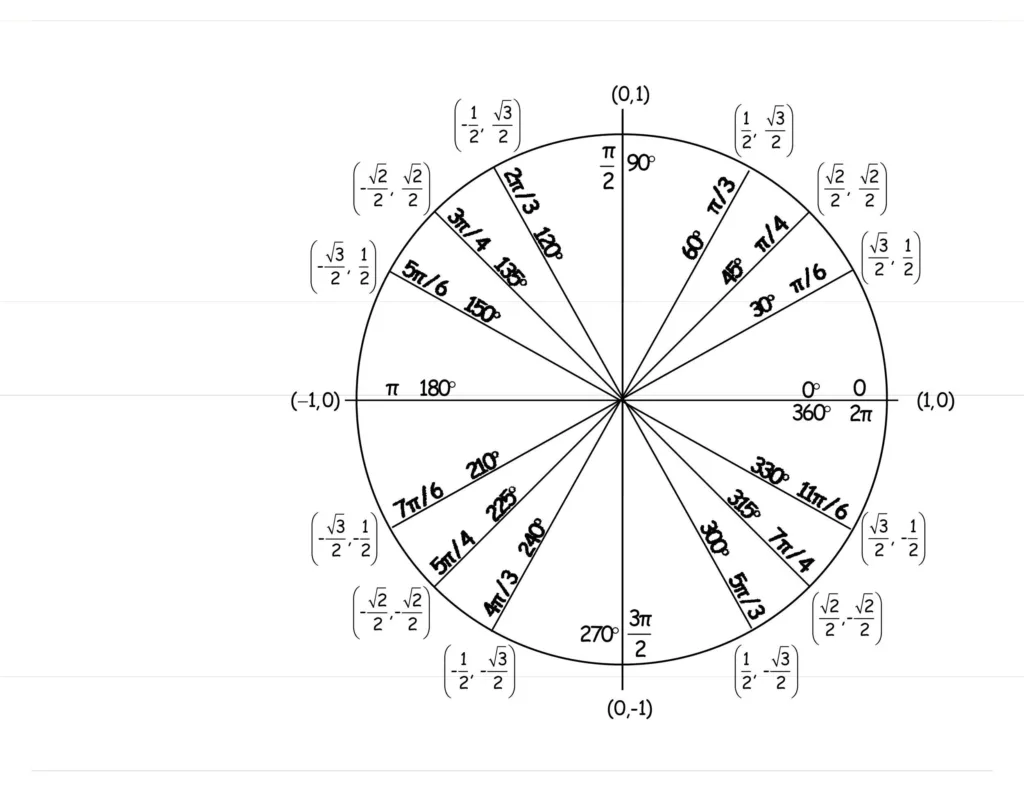
What is the Cotangent of an Angle?
Cotangent θ is a mathematical term used to describe the ratio of the adjacent side length to the opposite side length in a right angled triangle. It is represented by cot(θ) and can be calculated by dividing the length of the adjacent side by the length of the opposite side. Knowing this ratio can help you to calculate other angles and lengths in a right angled triangle, giving you more information about its shape and size.
Where Does Cotangent Equal -1 on the Unit Circle?
On the unit circle, the point at which cot = -1 is located in the third quadrant, at an angle of 135° or 3π/4 radians. This point lies on the upper half of the unit circle (the y-coordinate is positive) and can be seen in the diagram below. The angle is measured counterclockwise from the positive x-axis.
Difference Between Cotangent and Tan 1
No, cotangent (c o t) is not the same as tan-1. Cotangent is the inverse of a tangent function, meaning it is the ratio of the opposite side to the adjacent side of a right triangle. In contrast, tan-1 (also known as arctan) is a function that calculates the angle whose tangent is equal to a given number. Therefore, although both involve trigonometric functions, they do not have identical uses or results.
Comparing Cot and Cos
Cotangent (cot) is the reciprocal of the tangent, meaning it is the ratio of the adjacent side of a triangle to its opposite side. Cosine (cos) is the ratio of the adjacent side of a triangle to its hypotenuse, or longest side. In other words, cot is the inverse of tan, while cos is the inverse of sin.
What is Theta in Trigonometry?
In trigonometry, θ is a variable that represents an angle in a right triangle. It is often used to represent the acute angles of the triangle, which are the angles that are less than 90 degrees. By using the sine, cosine, and tangent of θ, it is possible to find information about the other sides of the right triangle such as their lengths and angles. Essentially, knowing θ allows us to solve for many other aspects of a right triangle.
Formula for Cotangent of an Angle
The formula of cot theta is quite simple and can be derived from basic trigonometric principles. Cot theta is defined as the ratio of the base, or side adjacent to an angle (theta), to the perpendicular, or side opposite to that angle. Mathematically this can be expressed as cot θ = Base/Perpendicular = cos θ/ sin θ. Therefore, in order to calculate cot theta for a given angle, you simply need to divide the cosine of that angle by its sine.
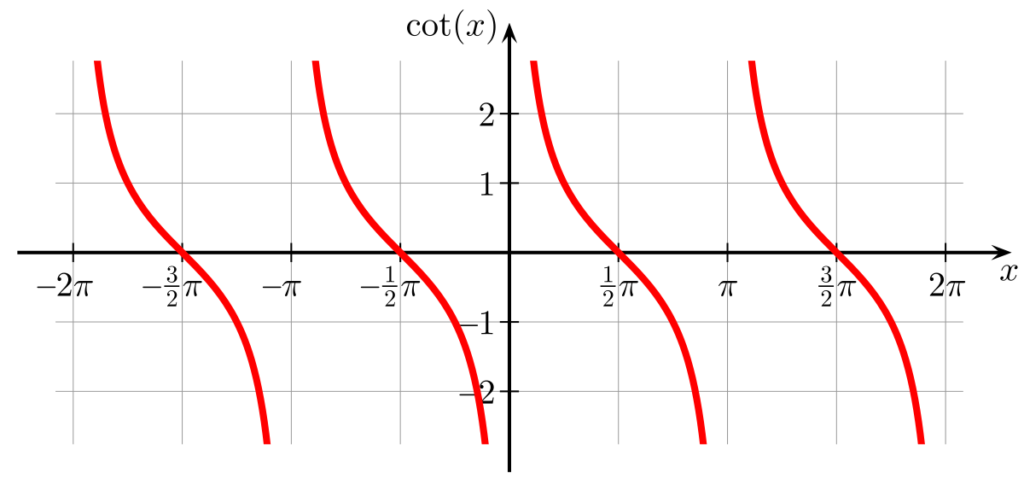
Period of Tan and Cot Functions
The period of the tangent (tan θ) and cotangent (cot θ) functions is π, meaning that after increasing the angle by π, the value of the function will repeat itself. This can be seen by plotting out the graphs of tan θ and cot θ, which both have repeating ‘waves’ with a period of π.
Is Cot Defined at 0?
Yes, cotangent is undefined at 0. This is because cotangent is the reciprocal of tangent, and the value of tangent at 0° is 0. Since any number divided by 0 is undefined, the cotangent of 0° must also be undefined.
Inverse of Cot Function
Cotangent (cot) is the inverse of the tangent function. In other words, it is the reciprocal of the tangent function, meaning that it produces the same angle when applied to a given ratio of two sides of a right triangle. When we take the cotangent of an angle, we are finding the ratio of the hypotenuse to the opposite side of a right triangle. This means that for any given angle, there will be a corresponding cotangent value that can be used to calculate distances beteen points in a triangle or on a graph. Cotangents can also be used to calculate unknown angles in a triangle when two sides are known.
Conclusion
In conclusion, the cotangent of a unit circle is an important mathematical concept that can be used to calculate angles or lengths of sides in right-angled triangles. The cotangent formula is used to find the cotangent of an angle corresponding to a point on the unit circle, which is defined as the ratio of the length of the adjacent side to the length of the opposite side. The range of cot- 1 is limited to (0, 180°) or (0, π). With this knowledge, it is now possible to understand and calculate angles and lengths in any given triangle with ease.
