Triangles are one of the most basic shapes in geometry, and they come in various forms. One such form is the isosceles triangle, which has two sides of equal length. Isosceles triangles are unique in that they have two congruent angles opposite the equal sides. This article will explore the properties of isosceles triangles and their applications.
The first property of an isosceles triangle is that it has two equal sides. These sides are referred to as legs, and the third side is called the base. The two legs meet at a point called the vertex angle. As previously mentioned, the two angles opposite the equal sides are equal. Therefore, if one angle is known, the other can be easily calculated.
The area of an isosceles triangle can be calculated uing the formula 1/2 base x height. The height is a line perpendicular to the base that reaches the vertex angle. The height can be calculated using the Pythagorean theorem. If the length of the legs is known, the height can be calculated by dividing the length of one leg by two and then using the Pythagorean theorem to find the height.
Isosceles triangles have many applications in various fields. Architects and engineers use isosceles triangles in designing buildings and structures. For example, a roof with an isosceles triangle shape can provide stability and balance to a building. In medicine, isosceles triangles are used in the measurement of blood pressure. The cuff that is placed around the arm to measure blood pressure is designed to form an isosceles triangle.
Isosceles triangles are a unique form of triangles that have two sides of equal length. They have many properties and applications in various fields. From architecture to medicine, isosceles triangles play an important role in our lives. Understanding the properties of isosceles triangles can lead to a better understanding of geometry and its applications.
What Triangle Has 2 Sides And 2 Angles Equal?
The type of triangle that has two sides and two angles equal is called an isosceles triangle. This means that the two sides opposite the equal angles are of equal length, while the third side may be of a differnt length. Isosceles triangles are commonly found in geometry and mathematics, and are used in various applications such as in architecture, engineering, and physics. Isosceles triangles can be easily identified by their unique properties, and are an important concept to understand in the study of geometry. Some common examples of isosceles triangles include the roof of a house, the sides of a tent, and the wings of an airplane.
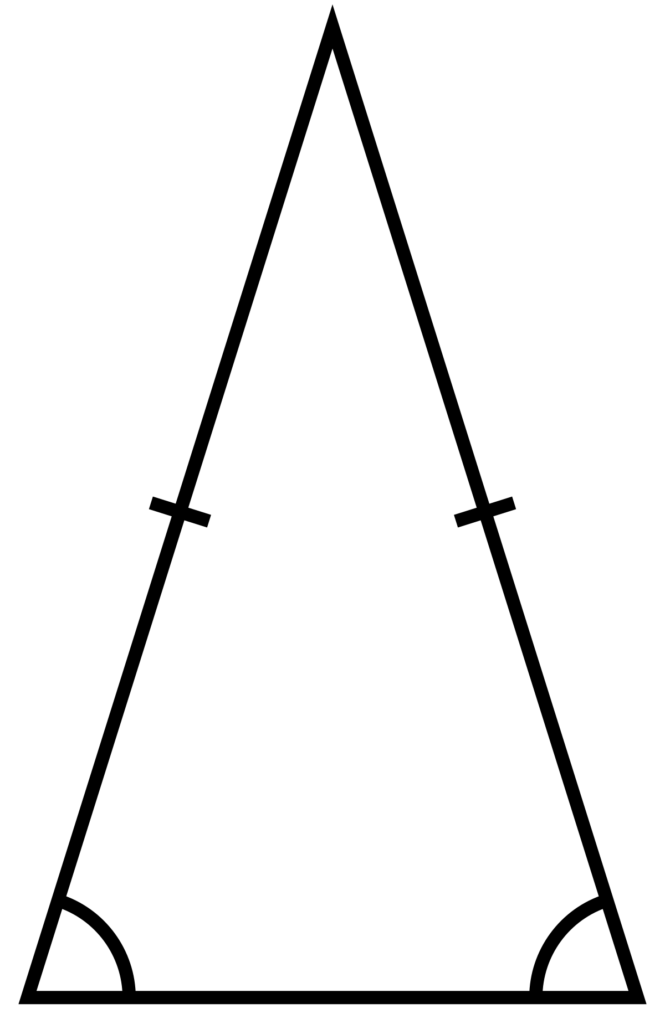
Is Isosceles Triangle Two Sides Are Equal?
An isosceles triangle is a type of triangle that has two sides of equal length. The other side of the triangle, called the base, may or may not be of a different length. The two equal sides are also referred to as legs, while the unequal side is the base. The two angles opposite the equal sides are also congruent or equal in measure. This means that if we know the length of the two equal sides, we can easily find the measure of the two equal angles using basic trigonometric functions such as sine, cosine, and tangent. It is worth noting that not all triangles are isosceles triangles, as tere are also scalene triangles and equilateral triangles which have different side lengths.
How Do You Find The Area Of A Triangle With 2 Equal Sides?
To find the area of an isosceles triangle with two equal sides, you need to know the height (altitude) and the base of the triangle. Once you have these measurements, you can use a simple formula to calculate the area. The formula to find the area of any triangle is:
Area = (1/2) x base x height
In the case of an isosceles triangle, the two equal sides form the base of the triangle, and the height is the perpendicular line drawn from the base to the opposite vertex. So, to find the area of an isosceles triangle, you simply need to multiply the length of one of the equal sides by the height, and then divide that number by two.
Here’s an example:
Suppose you have an isosceles triangle with two equal sides measuring 5 cm each and a height of 4 cm. To find the area, you wold use the formula:
Area = (1/2) x base x height
Since the base is made up of two equal sides, you can use either one of them in the formula. Let’s use 5 cm:
Area = (1/2) x 5 cm x 4 cm
Area = 10 cm²
So the area of this isosceles triangle is 10 square centimeters.
Conclusion
The isosceles triangle is a fundamental shape in geometry that has two equal sides and two equal angles. The symmetry of this triangle makes it useful in various fields, including architecture, engineering, and mathematics. The properties of an isosceles triangle make it easy to calculate its area, perimeter, and other geometric measurements. Additionally, the isosceles triangle plays a vital role in trigonometry, where it is used to derive formulas for solving complex problems. understanding the isosceles triangle is essential for anyone interested in geometry or mathematics, as it is a foundational shape that appears in many different contexts.
