Today, we’ll be taking a look at the cotangent formula and how it can be used in math. The cotangent of an angle is defined as the cosine of the angle divided by the sine of that angle. This formula is often written as cot x = cos x sin x.
The cotangent ratio is equal to the length of the adjacent side of an angle divided by the length of its opposite side, so it can also be written as cb x = c b or cot x = cbx. This ratio can also be expressed in terms of tan, which woud look like either cot θ = 1/tan θ or cot θ = tan (π/2 – θ).
In a right-angled triangle, the cotangent of an angle is equal to the length of its adjacent side divided by its opposite side. This formula can then be used to determine other sides and angles in a right-angled triangle if one side and one angle are known.
The tangent of an angle can also be determined using this formula; it is equal to the ratio of its opposite side over its adjacent side. Knowing this information allows you to calculate angles that you wouldn’t otherwise know how to solve for.
To wrap things up, let’s review what we’ve learned:
• The cotangent formula is written as either cot x = cos x sin x or cbx =c b
• In a right-angled triangle, it is equal to the length of its adjacent side divided by its opposite side
• It can also be expressed in terms of tan: either 1/tan θ or tan (π/2 -θ)
• The tangent formula is equal to the ratio of its opposite side over its adjacent side
• Knowing this information allows you to calculate angles that you wouldn’t otherwise know how to solve for
Hopefully this blog has cleared up any confusion about the cotangent formula and how it relates to triangles!
The Cot Formula
The cotangent formula is used to calculate the cotangent of a given angle. The cotangent of an angle is equal to the cosine of the angle divided by the sine of the angle. Mathematically, this can be expressed as cot x = cos x / sin x. To find the cotangent of an angle, one must first calculate the cosine and sine of that angle, then divide one by the other. As an example, if we have an angle θ with a cosine and sine equal to 0.5 and 0.866 respectively, then its cotangent would be calculated as 0.5/0.866 = 0.57735.
Source: commons.wikimedia.org
What is the Cotangent of an Angle θ?
Cotangent θ is a trigonometric ratio that measures the angle in a right-angled triangle. It is equal to the length of the adjacent side divided by the length of the side opposite the angle. This ratio can be expressed as cot(θ) = adjacent / opposite. It is important to note that cotangent θ is only applicable to right-angled triangles, as it relies on two sides with a 90 degree angle between them.
Formula for Cotangent of an Angle
The formula of cot θ is expressed in two ways. The first is cot θ = 1/tan θ. This means that the cotangent of an angle is equal to the reciprocal of the tangent of that angle. The second expression for cot θ is tan(90° – θ). This means that the cotangent of an angle is equal to the tangent of the supplementary angle (180° – θ). In both cases, cot θ can be calculated by taking the inverse (or reciprocal) of the tan θ value.
Finding the Cotangent of a Triangle
To find the cotangent of a triangle, you will first need to know the length of the sides adjacent and opposite to the angle in question. To calculate the cotangent ratio, divide the length of the adjacent side by the length of the opposite side. For example, if you have a triangle with an angle θ and two sides with lengths a and b, then the cotangent ratio would be written as cot θ = a/b. This will give you the ratio between these two sides for that particular angle.
The Meaning of Cot in Calculators
Cot, or cotangent, is a trigonometric function that is used to calculate the ratio of the lengths of the sides of a triangle. Cot can be used to calculate angles and sides of a triangle. In addition, cot can be used in more advanced calculations such as vectors and complex numbers. To use cot in a calculator, it is often expressed as COT(x), where x represents an angle expressed in radians. To convert degrees to radians you can use the RADIANS function. The output of COT(x) will be the cotangent of x.

Comparing Cot and Cos Functions
Cotangent (cot) and cosine (cos) are two of the main trigonometric functions used in mathematics. Cot is an inverse function of the tangent, which means that for every angle, the cotangent of that angle is equal to the reciprocal of its tangent. Cosine, on the other hand, is an inverse function of the sine, which means that for every angle, the cosine of that angle is equal to the reciprocal of its sine. The cotangent and cosine are related in that they both use angles to calculate a ratio between two sides of a right triangle.
The Meaning of θ in Trigonometry
In trigonometry, θ is an angle in a triangle. It is commonly known as the “theta” angle and is typically used to calculate the sides of a right triangle. Specifically, it is one of the acute angles in a triangle and its sine, cosine, and tangent can be calculated using the ratios of the opposite side to the hypotenuse and adjacent side to hypotenuse for sine and cosine respectively, and the ratio of opposite side to adjacent side for tangent.
What is the Meaning of θ in Mathematics?
In mathematics, θ (the Greek letter “theta”) is commonly used to represent an angle. Angles are usually measured in degrees, and θ is typically used as the symbol for an unknown angle measure. It is also sometimes used as a variable to indicate an arbitrary angle when solving equations or performing calculations involving angles.
The Value of Cotangent in Degrees
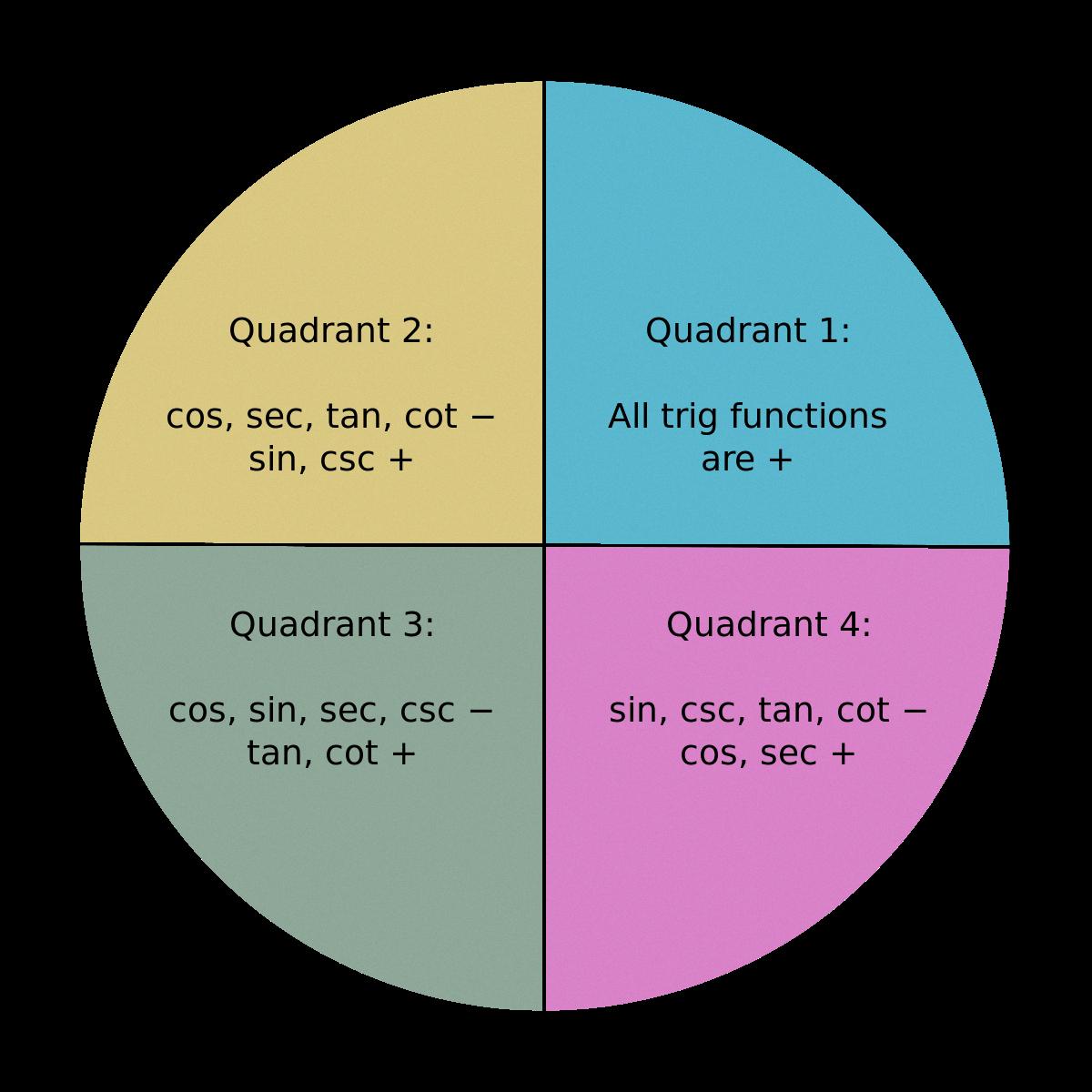
The value of cot (the ratio of the cosine and sine of an angle) for any given degree is equal to the ratio of the cosine of that angle and the sine of that angle. Thus, for any given degree, if we denote it as ‘x’, then cot (x) = cos (x) / sin (x). However, in cases where the sine of a given angle is equal to 0, then the value of cot is undefined or infinity (∞), since it would require taking a ratio where the denominator is equal to 0. This happens at 0°, 180° and 360°.

Source: intomath.org
Is the Cotangent the Inverse of the Tangent?
Yes, cot (cotangent) is the inverse of tan (tangent). Cotangent is the ratio of the adjacent side and hypotenuse of a right triangle, while tangent is the ratio of the opposite side and adjacent side. Since these two ratios are inverses of each other, it follows that cot is the inverse of tan.
Inverse of Cotangent
The inverse of the cotangent function, also known as arccot or inverse cotangent, is a mathematical function that takes the cotangent of a number and returns its angle in radians. The domain and range of the arccot function is -∞ < x < ∞, and 0 < y < π respectively. This means that for any given value of x, arccot can be used to find its corresponding angle in radians. To find the inverse cotangent of a number x, we use the equation y = cot-1x. This equation can be used to calculate the angle in radians for any given value of x.
Conclusion
In conclusion, the cotangent formula is an important tool used in trigonometry to calculate the cotangent of any angle. The formula can be written in varios ways, such as cot x = cos x sin x or cot θ = 1/tan θ. Additionally, it can also be written as cot θ = tan (π/2 – θ) or tan(90° – θ). The cotangent ratio is equal to the length of the adjacent side of the angle divided by the length of the opposite side of that angle, so cot x = cb x = c b. Knowing how to use this formula correctly will aid in understanding how to solve for angles and sides of a right triangle and other shapes.
