Are you confused about reference angles and whether or not they can be negative? Don’t worry, this blog post will help you understand them better.
Reference angles are a concept used in trigonometry and geometry to find the angle between a givn angle and the x-axis. In other words, it is the angle that is formed when the terminal side of an angle intersects with the x-axis. This angle is always positive, as it must be less than 90 degrees. For example, if we were to look at an angle of 225 degrees, then its reference angle would be 45 degrees (or π/4).
So can reference angles be negative? The answer is no. Reference angles must always be positive because they measure the rotation from the initial side to the terminal side in a counterclockwise direction, which results in a positive measurement. If measured in a clockwise direction, then the angle will be negative – but this is not considered a reference angle.
If you have an angle that is negative but want to find its coterminal (or equivalent) positive value then you can simply add 360° to it. For example, if you have an angle of -40° then its coterminal value would be 320° (360° + -40°).
Understanding reference angles and their properties can help make your math problems easier and more efficient to solve. So now that we have clarified what reference angles are and whether or not they can be negative, hopefully your trigonometry questions won’t seem so daunting anymore!
Is the Reference Angle Always Positive?
Yes, the reference angle is always positive. This is because it is the angle between the terminal side of an angle and the x-axis. The terminal side of an angle is always on one side of the x-axis, and so the reference angle must be less than 90° in order to remain on that same side. Therefore, it must be a positive value.
Reference Angle of Negative 400
The reference angle of negative 400 is 40°. This is because when angles are measured in the counterclockwise direction, the reference angle is equal to the absolute value of the angle subtracted from 360°. In this case, we subtract 400° from 360° to get a reference angle of 40°.
Can Angles in Standard Position Be Negative?
Yes, angles in standard position can be negative. In standard position an angle is measured from the positive x-axis (which is usually considered the reference line) and rotates counterclockwise. For example, a 90 degree angle in standard position is measured from the positive x-axis and rotates counterclockwise 90 degrees to end on the positive y-axis. However, if the angle is measured in a clockwise direction from the positive x-axis it would be considered negative. For example, if an angle rotates 270 degrees clockwise from the positive x-axis it would be -270 degrees in standard position.
Identifying Positive and Negative Angles
We can say that an angle is positive when it rotates in an anticlockwise direction, and negative when it rotates in a clockwise direction. This is measured using either the degree method or the radian method. Coterminal angles share the same terminal side, but have different signs depending on their rotation direction.
Identifying Positive and Negative Angles
Positive angles are measured in a counterclockwise direction, while negative angles are measured in a clockwise direction. To determine which angle is positive and which is negative when finding coterminal angles, start at the given angle and move either clockwise or counterclockwise until you reach the desired angle. If you move counterclockwise, the angle will be positive; if you move clockwise, the angle will be negative.
Reference Angle of Negative 300
The reference angle for negative 300 degrees is 60 degrees. This is because when you add 360 degrees to negative 300 degrees, the resulting angle of 60 degrees is positive and coterminal with negative 300 degrees. Since 60 degrees is in the first quadrant, the reference angle is also 60 degrees.
Reference Angle of Negative 150 Degrees
The reference angle of negative 150 degrees is 30 degrees. To determine the reference angle, we first need to convert the measure of the angle from negative degrees to radians. To do this, we can use the formula: Radians = (180/π)*degrees. Therefore, for -150°, we get -2.618 radians.
Next, we need to convert this back to an angle measure in degrees, as reference angles are aways measured in degrees. To do this, we use the formula: Degrees = (π/180)*radians. Therefore for -2.618 radians, we get 150°.
Finally, once we have our measure in degrees, all that is left to do is to find the reference angle by subtracting it from 180° and the reference angle for a -150 degree angle is 30°.
Reference Angle for Negative 220
The reference angle for negative 220 is 140°. This is because the closest multiple of 180° to negative 220 is -180°, and the reference angle is the difference between -180° and -220°, which is 140°.
Reference Angle of Negative 75 Degrees
The reference angle of negative 75 degrees is 105 degrees. This is because the reference angle is always measured from the positive x-axis and in the first quadrant. Since negative 75 degrees lies in the fourth quadrant, it has an angle of measurement of 285 degrees, relative to the positive x-axis. To calculate the reference angle, we subtract this from 360, which gives us a reference angle of 105 degrees.
Effects of a Negative Angle
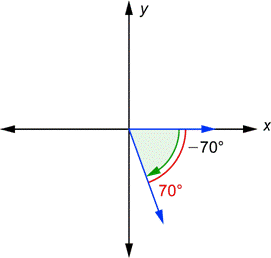
Negative angles are used when working with angular measurements, such as in trigonometry or geometry. In these contexts, a negative angle is one that is measured counterclockwise from the positive x-axis of a unit circle or Cartesian plane. For example, if an angle is -60°, it would be 60° below the x-axis and 300° above the x-axis. This can also be thought of as 360° minus 60°. Depending on the context and application, negative angles may have different effects or implications. In mathematics and physics, for example, a negative angle may change the sign of certain values or equations related to the angle.
The Meaning of a Negative Angle
A negative angle is a type of angle that has been rotated in a direction opposite to the conventional, usually clockwise, rotation. It is measured in degrees, just like any other angle. A negative angle is considered to be the same as 360 degrees minus the magnitude of the given angle, meaning it can range from 0° to -359°. To visualize this concept, imagine you are standing at 0° and move counterclockwise around a circle until you reach your desired negative angle. For example, if you were to move 270° counterclockwise from 0°, you would end up at -90°.
The Significance of Negative Angles
Some angles are negative because they turn in a clockwise direction instead of the expected counterclockwise direction. On the coordinate plane, angles that turn in a clockwise direction have an initial side that is below the positive x-axis. Negative angles also have a greater magnitude than their corresponding positive angles; for example, a -90° angle has a greater magnitude than a 90° angle. This is because when travelling around the unit circle, it takes longer to travel in a clockwise direction than it does to travel in a counterclockwise direction.
Conclusion
In conclusion, a reference angle is an angle measured from the x-axis to the terminal side of a given angle. It must be less than 90 degrees, and it is always positive. Reference angles are useful for simplifying calculations involving angles that have been rotated multiple times around the origin, as they allow us to find an equivalent angle with a reference of 0°.
