Welcome to our blog post about PDFs (Probability Density Functions) and whether or not they can be greater than 1. We’ll start by defining what a PDF is, and then move on to cover if they can be greater than 1.
A PDF is a mathematical function that describes the probability of obtaining a given value of a random variable. In other words, it is used to describe the likelihood of an event occurring and how it changes over time or space. A PDF assigns probabilities to intervals and not to single points. The area under the curve between two distinct points defines the probability for that interval, meaning that the height of the probability function can in fact be greater than one.
So, can PDFs exceed 1? The answer is yes! Remember that the integral of the pdf function over the domain of a random variable must equal one, which is the sum of all areas under the curve regardless of its density. This means that it is possible for certain values within a PDF to exceed 1- for example in a standard normal distribution (mean 0 and variance 1), this will occur when calculating specific values.
To summarise, PDFs are mathematical functions used to describe probabilities over intervals, not single points. The area under thse curves must equal one regardless of their density, meaning that it is possible for certain values within them to exceed 1. We hope this blog post has helped you understand more about PDFs and if they can be greater than 1 – thank you for reading!
Can Probability Density Values Exceed 1?
Yes, probability density can be greater than 1. This occurs when the probability of a specific outcome is higher than the probability of any other outcome. For example, if a coin is biased so that it has an 80% chance of coming up heads, then the probability density at the heads outcome would be greater than 1. Similarly, if two dice are rolled and one has an 80% chance of rolling a 5, then the probability density at 5 would be greater than 1. In these cases, the total area uder the curve (which is equal to 1) still holds since it is a summation of all probabilities between 0 and 1.
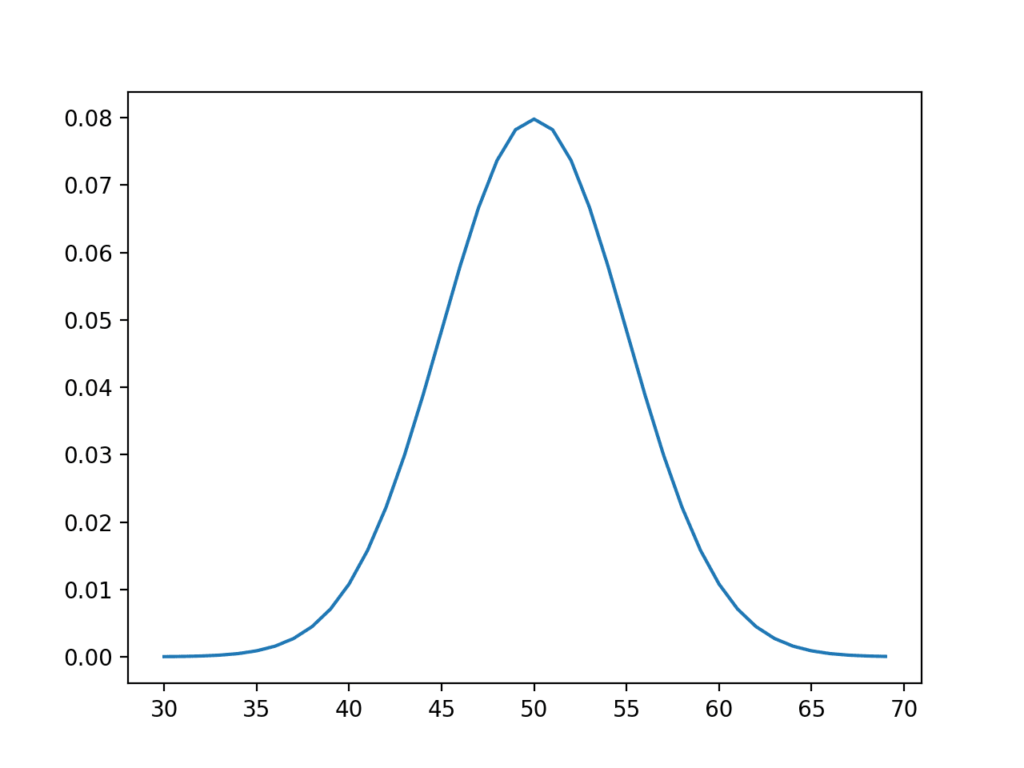
Can a Probability Distribution Exceed 1?
No, the probability of any single point can never be greater than 1. However, when looking at a probability distribution over an interval, the area under the curve can be greater than 1. This is because the total probability for that interval is not just limited to the height of the function at any single point. Instead, it is determined by the area under the curve betwen two points. For example, if you were to look at a probability distribution for rolling two dice and adding their values together, you would see that in some intervals (e.g., from 7 to 8) the area under the curve exceeds 1.
PDF Greater Than One Meaning
If the PDF (Probability Density Function) is greater than 1, it means that the relative probability of a given value of a random variable is higher than 1. This can happen if the curve representing the PDF is relatively steep at certain points, meaning that the probability of values in those regions is much higher than expected. In other words, it means that certain values are more likely to occur than others.
Can a Normal Distribution Have Values Greater Than 1?
Yes, normal distribution can be greater than 1. A normal distribution is a type of probability distribution that has a bell-shaped curve. It is defined by two parameters: the mean (μ) and the standard deviation (σ). The mean determines the center of the curve and the standard deviation determines how spread out the data is from the mean. The most commonly used normal distribution is called the standard normal distribution, wich has a mean of 0 and a standard deviation of 1. The probability density function (PDF) for this type of normal distribution has a maximum value of 1, which means that any values larger than this are possible when calculating a specific value in a general normal distribution PDF.
What to Do When Probability Is Greater Than 1
If your probability is greater than 1, it means that the chance of the event occurring is greater than 100%. This could happen for several reasons. Firstly, it is important to check if you have correctly calculated the probability. If you are sure that your calculation is correct, then it means that either one or more of your assumptions are wrong or the events that you are considering are not independent of each other.
In situations where your assumptions are incorrect, you need to re-evaluate them and make sure they accurately reflect the situation. If the events are not independent of each other then you need to consider how their outcomes may be linked and adjust the probability accordingly.
It is also possble that a probability can be greater than one due to rounding errors in calculations. In this case you should check your calculations and adjust them if necessary.
No matter what the cause, if your probability is greater than one it means that either your assumptions or calculations need to be reviewed in order to get an accurate result.

Density Greater Than 1: What Does It Mean?
If the density of a substance is greater than 1, it means that the substance is denser than the reference material. This means that for a given volume of the substance, there will be more mass than for the same volume of the reference material. For example, if water has a relative density of 1, and an unknown material has a relative density of 1.5, this would mean that for any given volume, the mass of the unknown material would be 50% greater than the mass of water for that same volume.
Can PDFs Have No End?
Yes, a PDF can be infinite. A PDF (Probability Density Function) is a mathematical equation that describes the probability of an event occurring witin a given range of values. The PDF assigns probabilities to all values within the range, which can include an infinite number of possible outcomes. This means that the PDF can have an infinite limit when its probability is distributed over all possible values.
For example, consider a normal distribution with mean 0 and variance 1. The probability density for this distribution is defined by the equation: f(x) = e^(-x^2/2)/√2π. In this case, the probability density is spread out infinitely over all possible values, from -∞ to +∞, making it an infinite PDF.
In general, any continuous probability distribution with an unbounded range has the potential to be infinite if its probability density is distributed across all possible values in its domain.
Can the Cumulative Distribution Function Exceed a Value of 1?
No, CDF cannot be greater than 1. The cumulative distribution function (CDF) is a probability measure that gives the probability of observing a value at or below a certain threshold. It ranges from 0 to 1 and is non-decreasing, which means that the probability of observing a greater value increases as we move from left to right along the x-axis. Since no probability can be greater than 1, the CDF cannot be greater than 1 either.
What Happens When the Z Score Is Greater Than 1?
If the z score is greater than 1, it means that the raw score is more than one standard deviation above the mean. This indicates that the raw score is higher than what would normally be expected, and could suggest that the individual performing the task has an unusually high level of performance.
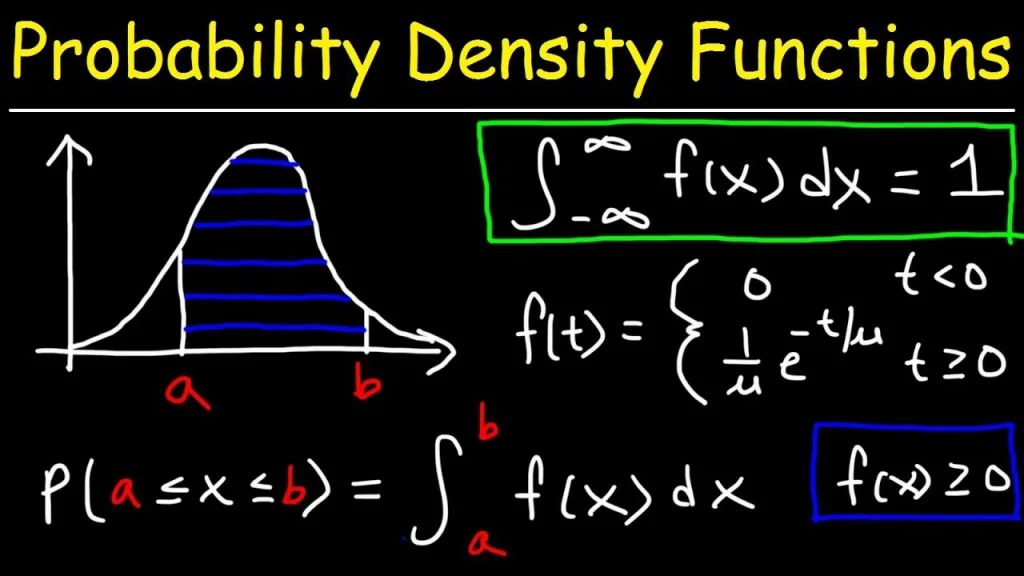
Negative Impact of PDFs
No, pdfs (probability density functions) cannot be negative. PDFs are mathematical functions that describe the probability of a random variable taking on a given value. By definition, the probability of any event is always greater than or equal to zero, so it follows that a PDF can never be negative. Furthermore, if the derivative of a PDF is taken, then it becomes a CDF (cumulative distribution function), which by definition must always be non-decreasing and therefore its derivative must also always be non-negative.
Conclusion
In conclusion, a Probability Density Function (PDF) is a function that describes the probability of a random variable taking on a given value. It is important to note that the PDF can exceed 1 since it represents the area under the curve of the probability distribution and not the height of any single point. The integral of the PDF over its domain must be equal to one in order for it to be a valid probability distribution. Thus, PDFs are a useful tool for understanding and predicting probabilities in various scenarios.
