When it comes to understanding waves and their properties, the concept of amplitude is crucial. The amplitude of a wave is defined as the maximum distance between a point on the wave and its equilibrium position. In simpler terms, it refers to the maximum displacement from the equilibrium that an object in periodic motion shows. In this blog post, we will dive deeper into the formula for amplitude and explore its vaious applications.
The formula for amplitude depends on the type of wave being analyzed. For instance, in the case of a sine wave, the formula for amplitude is given as follows:
X = A sin (ωt + ϕ)
Here, x represents the displacement of the wave, A represents the amplitude, ω represents the angular frequency, t represents time, and ϕ represents the phase angle.
Similarly, in the case of a cosine wave, the formula for amplitude is given as follows:
X = A cos (ωt + ϕ)
Here, x represents the displacement of the wave, A represents the amplitude, ω represents the angular frequency, t represents time, and ϕ represents the phase angle.
To understand the concept of amplitude better, let’s take the example of a pendulum. A pendulum swings through its equilibrium point (straight down), and then swings to a maximum distance away from the center. The amplitude of the pendulum would be the maximum distance it swings away from the center. This can be found by measuring the vertical distance between the maximum or minimum point and the equilibrium of the graph.
In the case of sound waves, the amplitude refers to the maximum displacement of a particle from its equilibrium position as the sound wave passes through it. The amplitude of a sound wave determines its loudness, with higher amplitudes corresponding to louder sounds.
The concept of amplitude finds applications in various fields, including physics, engineering, and music. Some of the key applications are:
1. Physics: The amplitude of a wave plays a crucial role in determining its energy. Waves with higher amplitudes have more energy than waves with lower amplitudes.
2. Engineering: In the field of engineering, the concept of amplitude is used to measure the strength of vibrations. For instance, the amplitude of vibrations in a building can be measured to determine its structural integrity.
3. Music: In music, the amplitude of a sound wave determines its volume. By adjusting the amplitude, musicians can create a range of different sounds and effects.
The formula for amplitude is an essential concept in understanding waves and their properties. It helps us to measure the maximum displacement of a wave from its equilibrium position and plays a crucial role in determining the energy and strength of waves. By understanding the formula for amplitude, we can gain a deeper insight into the behavior of waves and their applications in various fields.
Calculating Amplitude
In physics, amplitude is the measure of the maximum displacement of a wave from its equilibrium position. It is a crucial parameter in understanding the behavior of waves and their properties. The calculation of amplitude can be done using a simple formula, which is based on the specific wave function.
The general form of a wave function can be written as x = A sin (ωt + ϕ) or x = A cos (ωt + ϕ), were A represents the amplitude, ω is the angular frequency, t is the time, and ϕ is the phase angle. The angular frequency is related to the frequency of the wave by the formula ω = 2πf, where f is the frequency.
To calculate the amplitude of a wave, we need to measure the maximum displacement of the wave from its equilibrium position. This can be done by measuring the distance from the centerline to the peak or trough of the wave. The amplitude is equal to this distance.
Alternatively, if we know the wave function, we can directly calculate the amplitude using the formula A = x/ sin (ωt + ϕ) or A = x/ cos (ωt + ϕ), where x is the displacement of the wave from its equilibrium position at a specific time t.
The amplitude of a wave can be calculated by measuring the maximum displacement of the wave from its equilibrium position or by using the wave function formula and measuring the displacement at a specific time. It is an important parameter that helps us understand the behavior and properties of waves.
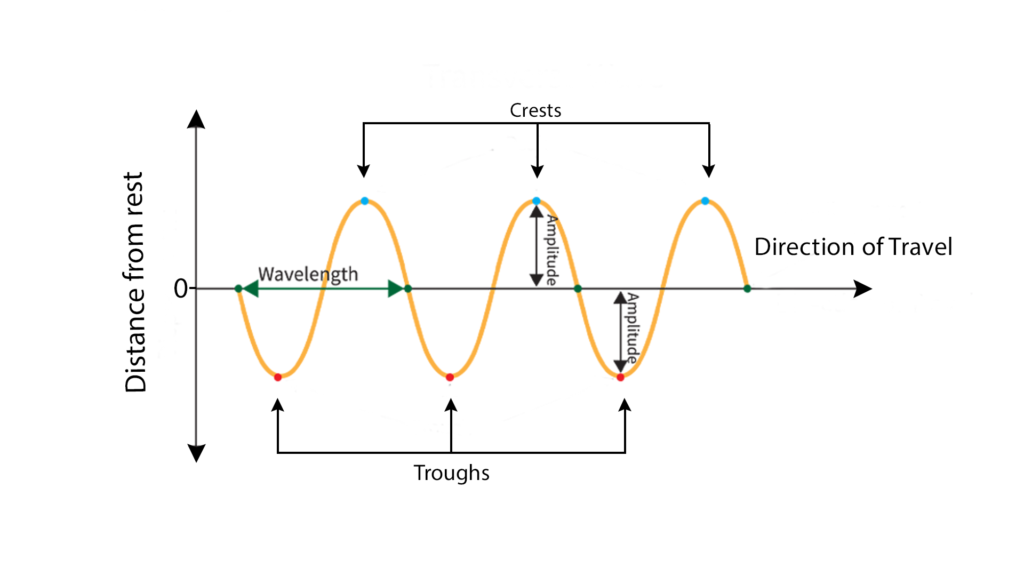
Finding the Amplitude of a Wave
The amplitude of a wave can be found by measuring the maximum distance between a point on the graph of the wave and its equilibrium. The equilibrium is the position where there is no displacement from the mean position. The amplitude is measured vertically from the equilibrium to either the crest or the trough of the wave. The crest is the highest point on the wave, while the trough is the lowest point on the wave.
To calculate the amplitude of a wave, you need to first identify the equilibrium position. This can be done by finding the mean position of the wave, whih is the point where the wave is at rest. Once you have identified the equilibrium position, you can then measure the distance from the equilibrium to either the crest or the trough. This distance is the amplitude of the wave.
It is important to note that the amplitude is a measure of the energy of the wave. The greater the amplitude, the more energy the wave has.
The amplitude of a wave can be found by measuring the maximum distance between a point on the graph of the wave and its equilibrium. The amplitude is measured vertically from the equilibrium to either the crest or the trough of the wave, and it is a measure of the energy of the wave.
Examples of Amplitude
Amplitude is a term used in physics to descrbe the maximum displacement or distance from the equilibrium point that an object in periodic motion exhibits. The equilibrium point is the point at which the object is at rest or in its natural position.
Amplitude is usually represented by the letter “A” and is measured in units such as meters or centimeters, depending on the type of motion being considered.
A simple example of amplitude is the motion of a pendulum. A pendulum is a weight suspended from a fixed point that swings back and forth in a regular motion. The maximum distance that the pendulum swings away from its resting position is its amplitude.
Another example of amplitude is the oscillation of a spring. When a spring is pulled or compressed and then released, it oscillates back and forth around its equilibrium position. The amplitude of the spring’s motion is the maximum distance it moves away from its resting position when it oscillates.
Amplitude is a fundamental concept in physics that helps describe the maximum displacement or distance from the equilibrium point that an object in periodic motion exhibits.
Formula for Calculating the Amplitude of Oscillation
The amplitude of oscillation formula is given by x(t) = A cos(ωt + φ), where A represents the amplitude of the oscillation. The amplitude is the maximum displacement of the object from its equilibrium position, in either the positive or negative x-direction. In other words, it is the distance from the equilibrium position to the maximum displacement of the oscillating object.
The formula describes the motion of a simple harmonic oscillator, which is a system that oscillates with a single frequency and exhibits sinusoidal motion. The amplitude is an important parameter in describng the behavior of the oscillator, as it determines the maximum potential energy stored in the system.
It is important to note that the amplitude of oscillation is independent of the frequency of the oscillation. However, the amplitude does affect the period and frequency of the motion, as well as the maximum kinetic and potential energy of the system.
The amplitude of oscillation formula is x(t) = A cos(ωt + φ), where A represents the maximum displacement of the oscillating object from its equilibrium position.
Understanding Amplitude in Physics
In the realm of physics, amplitude is a crucial concept that descries the maximum displacement or distance traveled by a point on a vibrating body or wave, measured from its equilibrium position. It is a fundamental characteristic of waves and vibrations, and understanding it is essential to comprehend a wide range of physical phenomena.
To put it simply, amplitude is the height of a wave or the distance between the crest (the highest point of the wave) and the trough (the lowest point of the wave). It is a measure of the energy carried by a wave and determines the intensity of the wave’s motion. The larger the amplitude, the more energy the wave carries.
Amplitude is typically measured in meters (m) or other units of length, and it is equal to one-half of the length of the vibration path. In other words, if a wave travels a distance of 2 meters from its equilibrium position, its amplitude would be 1 meter.
Amplitude is a critical factor in many physical phenomena, including sound waves, electromagnetic waves, and seismic waves. In sound waves, the amplitude determines the volume of the sound, with larger amplitudes producing louder sounds. Similarly, in electromagnetic waves, the amplitude determines the brightness of the light or the intensity of the radiation.
To sum up, amplitude is a fundamental concept in physics that describes the maximum displacement or distance traveled by a point on a vibrating body or wave. It is a measure of the energy carried by a wave and determines the intensity of the wave’s motion. Understanding amplitude is essential to comprehend a wide range of physical phenomena.
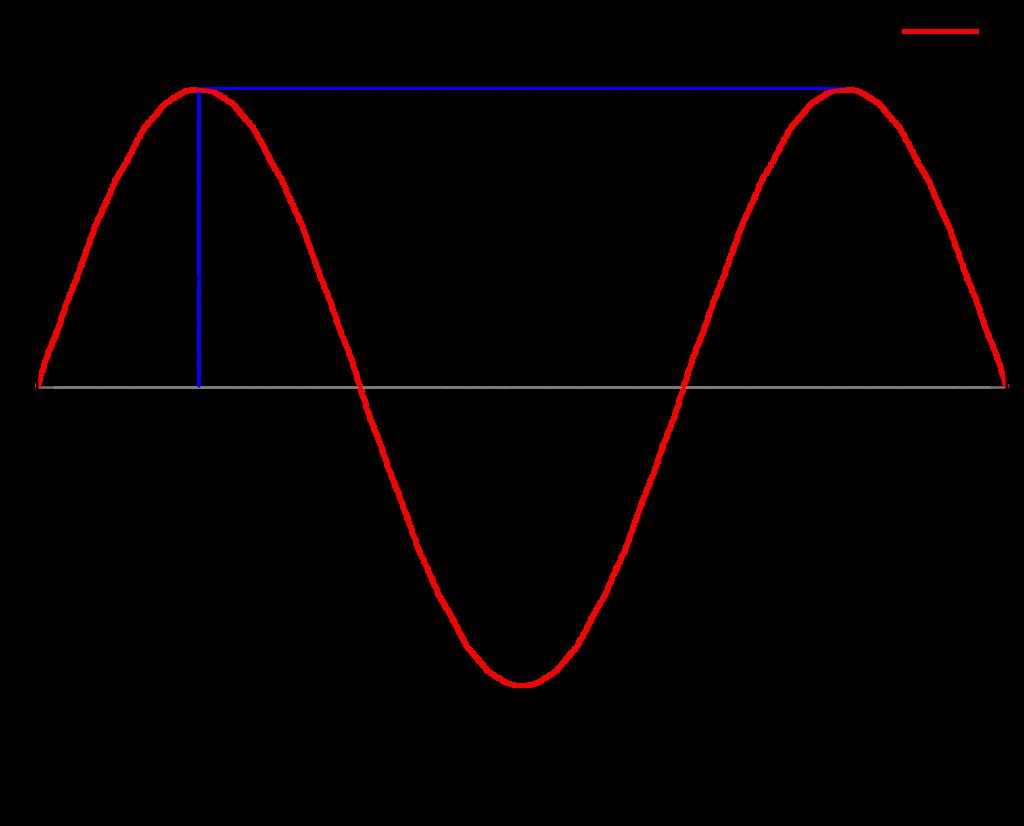
Source: toppr.com
The Unit of Measurement for Amplitude
Amplitude is a physical quantity that is used to describe the magnitude or strength of a wave. It is measured in units of distance, specifically in metres (m). The amplitude of a wave is defined as the maximum displacement of a particle from its equilibrium position during one cycle of the wave.
The greater the amplitude of a wave, the more energy it is carrying. This is because the amplitude represents the amount of energy that is being transferred by the wave per unit time. For example, a wave with a large amplitude will produce a louder sound or a brighter light than a wave with a smaller amplitude.
It is important to note that the amplitude of a wave is different from its frequency and wavelength. The frequency of a wave is the number of cycles it completes per unit time and is measured in Hertz (Hz). The wavelength of a wave, on the othr hand, is the distance between two consecutive points on the wave that are in phase with each other. It is also measured in metres (m).
The amplitude of a wave is a measure of its strength and is measured in metres (m). It is one of the three main characteristics of a wave, along with frequency and wavelength.
Finding the Amplitude of a Waveform
The easiest way to find the amplitude is by measuring the distance from the center line to the highest point (peak) or lowest point (trough) of a wave. This distance will give you the amplitude value. Alternatively, you can measure the height from the highest point to the lowest point and divide it by two to obtain the amplitude. It is important to note that the amplitude is a crucial parameter in determining the energy of a wave. It represents the maximum displacement of the medium from its equilibrium position. the easiest way to find the amplitude is to measure the distance from the center line to the peak or trough of a wave or to measure the height from the highest point to the lowest point and divide it by two.
Understanding Amplitude in Frequency
In the field of sound waves, amplitude and frequency are both important parameters to consider. Amplitude is defined as the maximum displacement of the particles in a sound wave from their average position. This means that it measures the distance that a particle moves back and frth from its resting position. The amplitude of a sound wave is directly related to its loudness, with larger amplitudes producing louder sounds.
On the other hand, frequency is the number of vibrations that a sound wave makes per second. This means that it measures the speed at which the particles in a sound wave are vibrating. The frequency of a sound wave is directly related to its pitch, with higher frequencies producing higher-pitched sounds.
While amplitude and frequency are distinct parameters, they are closely related in the sense that they both play a role in determining the overall characteristics of a sound wave. A sound wave with a high amplitude and low frequency, for example, will be loud and have a low pitch. Conversely, a sound wave with a low amplitude and high frequency will be quiet and have a high pitch.
To summarize, amplitude and frequency are both crucial components of sound waves. Amplitude refers to the maximum displacement of particles in a sound wave, while frequency refers to the number of vibrations the wave makes per second. Together, these parameters determine the sound’s loudness and pitch.
Understanding the Meaning of Amplitude in Math
In mathematics, the amplitude refers to the maximum displacement of a function from its equilibrium or midline. It is a measure of how far the graph of a function travels above and below its average value.
For example, in a sine function, the amplitude is equal to the coefficient of the sine term. If we have a sine function of the form y = A sin (Bx + C), where A is the amplitude, B is the frequency, and C is the phase shift, then the amplitude is simply the value of A.
The amplitude is an important concept in many areas of mathematics and science, including physics, engineering, and signal processing. In physics, it is used to descrbe the maximum displacement of a wave from its equilibrium position. In engineering, it is used to describe the maximum displacement of a vibrating system from its resting position.
Furthermore, the amplitude can be positive or negative, depending on the direction of the displacement. If the function oscillates above and below the midline, the amplitude is positive. If the function oscillates below the midline, the amplitude is negative.
To summarize, the amplitude is a measure of the maximum displacement of a function from its equilibrium or midline. It is an essential concept in many mathematical and scientific fields, and its value can be determined from the coefficient of the sine or cosine term in a periodic function.

Symbol for Amplitude
In the context of one dimensional motion, amplitude is a fundamental property of an oscillatory system. It refers to the maximum displacement of the system from its equilibrium position. The symbol used to represent amplitude is A, which is italicized and in capital letters. The SI unit of amplitude is the meter (m), but other units of length may be used depending on the context.
Amplitude is a crucial parameter in varius fields, including physics, engineering, and mathematics. It is used to describe the behavior of waves, vibrations, and other oscillatory phenomena. In particular, amplitude is a critical factor in determining the energy of an oscillating system.
To summarize, the symbol for amplitude is A, and it represents the maximum displacement of an oscillating system from its equilibrium position. The SI unit of amplitude is meters, but other units of length may be used.
Understanding Amplitude and Magnitude
In the world of physics and mathematics, amplitude and magnitude are two commonly used terms that refer to different aspects of a quantity. Amplitude can be defined as the maximum deviation from zero that can be taken by a periodically varying quantity. Magnitude, on the other hand, refers to the size of a quantity regrdless of the direction.
To understand the concept of amplitude, let’s take an example of a sound wave. The amplitude of a sound wave is the maximum displacement of the air molecules from their equilibrium position as the wave passes through them. In other words, it is the height of the wave’s crest or the depth of its trough. The larger the amplitude of a sound wave, the louder it will be perceived by our ears.
Similarly, in the case of an electromagnetic wave, the amplitude refers to the strength of the electric and magnetic fields that make up the wave. The larger the amplitude of an electromagnetic wave, the more energy it carries.
Magnitude, on the other hand, is a term used to describe the size of a quantity. Unlike amplitude, magnitude does not depend on the direction of the quantity. For example, the magnitude of a vector quantity, such as velocity or force, is the length of the vector. It is a scalar quantity that only takes into account the size of the vector, not its direction.
While amplitude and magnitude both describe the characteristics of a quantity, they refer to different aspects of it. Amplitude refers to the maximum deviation from zero that a periodically varying quantity can take, while magnitude refers to the size of a quantity regardless of the direction.
Measuring the Amplitude of Motion
In physics, the amplitude of motion is defined as the maximum displacement or distance that an object moves from its equilibrium position to either side. It is the distance from the center of motion to either of the extremes. For example, in the case of a pendulum, the amplitude woud be the maximum angle that the pendulum swings away from its vertical position. The amplitude is a crucial parameter that determines the energy of the system, and it influences the frequency and period of the motion as well. A higher amplitude will result in a higher maximum velocity and acceleration, which will affect the overall behavior of the system. Therefore, understanding the amplitude of motion is essential for analyzing and predicting the behavior of any oscillating system.
Understanding the Amplitude of Oscillation
In physics, amplitude refers to the maximum displacement or distance of an oscillating system from its equilibrium position during one complete cycle of motion. It is a fundamental property of any oscillating system, and its value determines the strength or intensity of the oscillation.
For example, in the case of a simple pendulum, the amplitude is the maximum angle that the pendulum swings away from its resting position. In the case of sound waves, the amplitude is the maximum variation in air pressure from the normal atmospheric pressure as the wave passes through a medium.
Amplitude is uually measured in units of length, such as meters or centimeters, or in units of pressure, such as pascals or decibels. The amplitude of an oscillation is directly proportional to the amount of energy involved in the oscillation, and therefore, it is an important factor in determining the behavior of the system.
Amplitude is a key concept in the study of oscillating systems, and it refers to the maximum displacement or distance of the system from its equilibrium position during one complete cycle of motion.
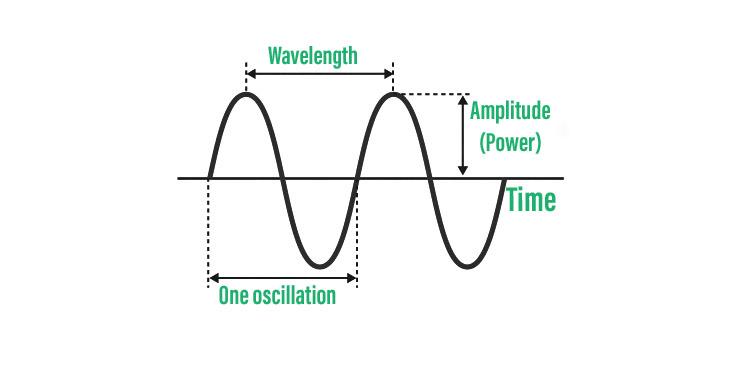
Source: geeksforgeeks.org
Conclusion
As we have discussed, amplitude is a crucial concept in the study of periodic motion. It refers to the maximum displacement of an object from its equilibrium position, either in the positive or negative direction. The formula for amplitude in simple harmonic motion is x = A sin (ωt + ϕ) or x = A cos (ωt + ϕ), where A represents the amplitude of the oscillation.
It is important to note that the amplitude is directly proportional to the energy of the system. The greater the amplitude, the more energy is required to sustain the motion. Therefore, understanding amplitude is essential in the analysis of various systems, including pendulums, springs, and waves.
Amplitude plays a crucial role in the study of periodic motion. It represents the maximum displacement of an object from its equilibrium position and is directly proportional to the energy of the system. By understanding the formula for amplitude, we can gain a btter understanding of the behavior of various systems and phenomena.
