The cross product is a fundamental concept in vector algebra that is used to calculate the vector perpendicular to two gven vectors. One of the interesting properties of the cross product is its distributivity over vector addition. This means that the cross product of a vector with the sum of two other vectors is equal to the sum of the cross products of the vector with each of the other vectors individually. In other words, if A, B, and C are vectors, then:
A × (B + C) = (A × B) + (A × C)
This property has important implications in physics and engineering, where it is often used to simplify calculations involving vector quantities.
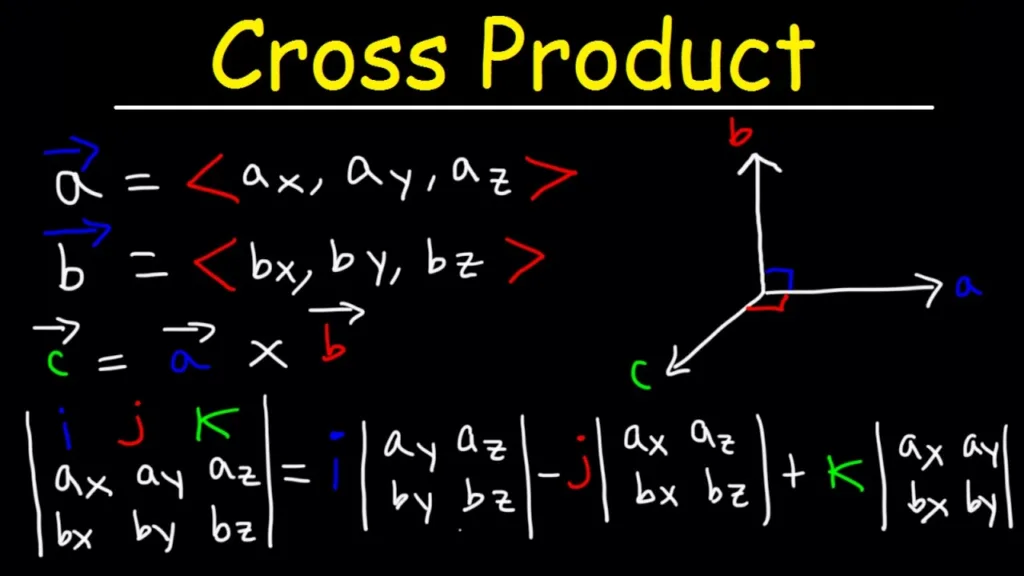
To see why the cross product is distributive, let us first recall the definition of the cross product. Given two vectors A = (Ax, Ay, Az) and B = (Bx, By, Bz), their cross product A × B is defined as:
A × B = (AyBz – AzBy, AzBx – AxBz, AxBy – AyBx)
Now, let us consider the expression A × (B + C). Using the definition of the cross product, we have:
A × (B + C) = (Ay(Bz+Cz) – Az(By+Cy), Az(Bx+Cx) – Ax(Bz+Cz), Ax(By+Cy) – Ay(Bx+Cx))
Expanding this expression, we get:
A × (B + C) = (AyBz – AzBy + AyCz – AzCy, AzBx – AxBz + AzCx – AxCz, AxBy – AyBx + AxCy – AxCy)
Notice that the terms AyCz and AzCy cancel out with each other, as do the terms AzCx and AxCz, and AxCy and AyBx. What is left is:
A × (B + C) = (AyBz – AzBy, AzBx – AxBz, AxBy – AyBx) + (AyCz – AzCy, AzCx – AxCz, AxCy – AxCy)
Comparing this to the expressions for (A × B) and (A × C), we see that this is equal to:
(A × B) + (A × C)
Therefore, we have shown that the cross product is distributive over vector addition.
It is worth noting that the distributivity of the cross product is analogous to that of the dot product. The dot product of two vectors A and B is distributive over vector addition in the sense that:
A · (B + C) = (A · B) + (A · C)
However, unlike the cross product, the dot product is also commutative and associative.
The distributivity of the cross product is a useful property that simplifies calculations involving vector quantities. It allows us to break down complex vector operations into simpler ones, and it has important applications in physics and engineering.
Does the Cross Product Distribute?
The cross product distributes acros vector addition. This means that for vectors a, b, and c, the following property holds true:
A x (b + c) = (a x b) + (a x c)
This property is similar to the distributive property of multiplication over addition in regular arithmetic. It allows us to simplify expressions involving cross products and vector addition.
It’s worth noting that the cross product is not commutative, which means that the order of the vectors matters. Specifically, for vectors a and b, we have:
A x b ≠ b x a
This property distinguishes the cross product from the dot product, which is commutative.
Associativity of the Cross Product
The cross product is a mathematical operation that takes two vectors and produces a third vector that is perpendicular to both of the original vectors. While the cross product has many useul properties, one property that it does not have is associativity.
To be more specific, the cross product is not associative, which means that the order in which you take the cross product of three or more vectors matters. In other words, if you have three vectors A, B, and C, then (A x B) x C is not necessarily equal to A x (B x C).
This lack of associativity can be demonstrated by choosing specific vectors for A, B, and C and calculating both expressions. For example, let A = (1, 0, 0), B = (0, 1, 0), and C = (0, 0, 1). Then, (A x B) x C = (0, 0, 1) x (0, 0, 1) = (0, 0, 0). On the other hand, A x (B x C) = (1, 0, 0) x (0, 0, 1) = (0, -1, 0), which is not equal to (0, 0, 0).
The cross product is not associative, meaning that the order in which you take the cross product of three or more vectors matters.
Does Cartesian Product Distribute Over Union?
The Cartesian product is a popular operation in set theory and mathematics that involves combining two sets to form a new set. When we talk abot the distribution of a Cartesian product, we are referring to a property that allows us to distribute the product operation over other set operations, such as union, intersection, and subtraction.
To be more specific, the distribution property of Cartesian product states that the Cartesian product of a set A with the union of two sets B and C is equal to the union of two Cartesian products of A with B and A with C. In other words, we can write the following equation:
A × ( B ∪ C ) = ( A × B ) ∪ ( A × C )
This property can be helpful in simplifying and solving complex mathematical problems involving sets and Cartesian products. It allows us to break down complex expressions into simpler components and apply the distributive law to simplify calculations.
It is worth noting that the distribution property of Cartesian product also applies to other set operations, such as intersection and subtraction. For example, we can write:
A × ( B ∩ C ) = ( A × B ) ∩ ( A × C )
And
A × ( B \ C ) = ( A × B ) \ ( A × C )
The Cartesian product does indeed distribute over union, intersection, and subtraction, and this property can be useful in simplifying mathematical expressions involving sets and Cartesian products.
Conclusion
We can say that the cross product is ineed distributive over vector addition, just like the dot product. This means that for any three vectors u, v, and w, we have (u x (v + w)) = (u x v) + (u x w). However, it is important to note that the cross product is not commutative, and it is not associative either. Additionally, we cannot say that multiplication of a vector by a scalar is distributive, as this is not a property of the cross product. understanding the distributive property of the cross product is crucial in many applications of vector algebra, such as in physics and engineering.
