Today, we will be discussing the differences beween exponential and linear functions. While both types of functions are used in various fields, including economics, biology, and physics, they operate very differently.
Let’s start with linear functions. Linear functions are used to model situations where there is a constant rate of change. This means that the output (y) changes by a fixed amount for every increase in input (x). Linear functions are often used to model simple situations such as distance traveled over time or income over years of employment. The equation for a linear function is y = mx + b, where m is the slope (the rate of change) and b is the y-intercept (the starting point).
On the other hand, exponential functions are used to model situations where there is a constant rate of growth or decay. This means that the output (y) changes by a fixed percentage for every increase in input (x). Exponential functions are used to model more complex situations such as population growth, radioactive decay, or compound interest. The equation for an exponential function is y = ab^x, where a is the initial amount, b is the growth/decay factor, and x is the time or number of generations.
The key difference between linear and exponential functions is the rate of change. In a linear function, the rate of change is constant, whereas in an exponential function, the rate of change increases or decreases over time. This means that in exponential functions, the output can increase or decrease rapidly, while in linear functions, the output changes at a steady pace.
Let’s look at an example to compare the two types of functions. Suppose we have a bank account that earns 5% interest every year. If we want to model the balance of the account over time, we would use an exponential function. The equation would be y = 1000(1.05)^x, where y is the balance, 1000 is the initial deposit, and 1.05 is the growth factor. After 1 year, the balance would be $1,050. After 5 years, the balance would be $1,276.28. Notice how the balance increases more rapidly as time goes on.
Now suppose we want to model the distance traveled by a car driving at a constant speed of 60 mph. We would use a linear function. The equation would be y = 60x, where y is the distance and x is the time in hours. After 1 hour, the car would have traveled 60 miles. After 5 hours, the car would have traveled 300 miles. Notice how the distance increases at a steady pace.
Linear functions are used to model situations with a constant rate of change, while exponential functions are used to model situations with a constant rate of growth or decay. The key difference between the two types of functions is the rate of change, with linear functions changing at a steady pace and exponential functions changing more rapidly over time. Understanding the differences between these two types of functions is important in a variety of fields and can help us make more accurate predictions about the future.
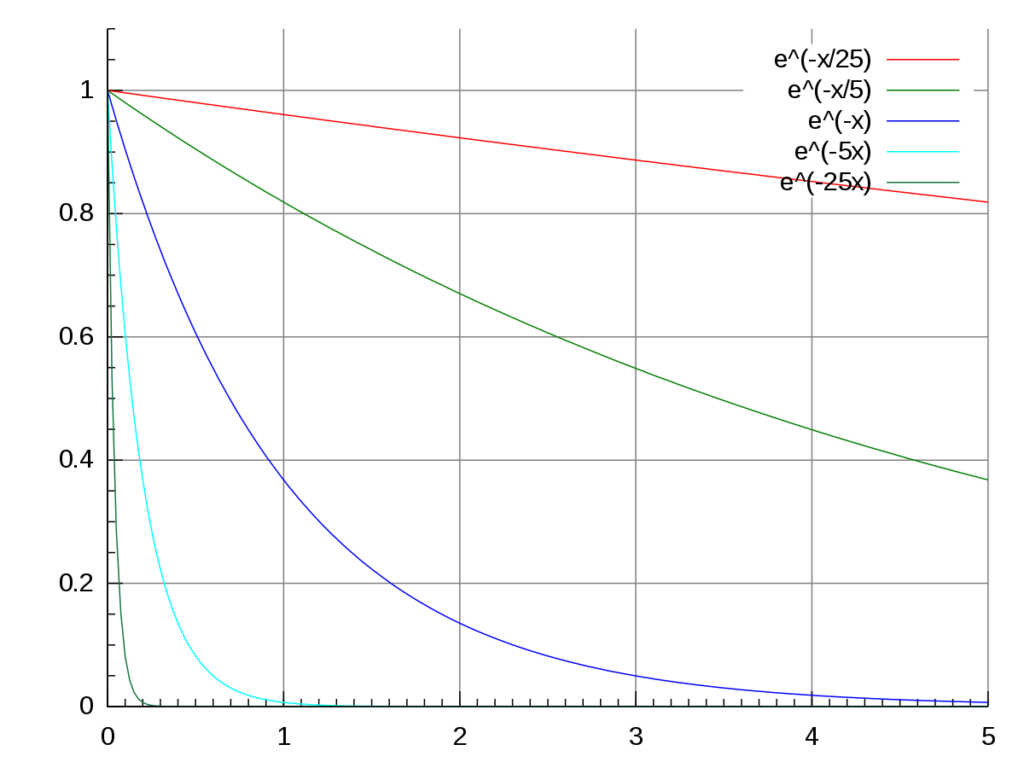
The Difference Between Exponential and Linear Decay
Exponential decay and linear decay are two distinct mathematical concepts used to describe the decrease in value over time. Exponential decay is characterized by a decay factor that is a percentage of the original amount, resulting in a decreasing rate of change over time. This means that as time progresses, the actual amount by wich the original value is reduced will change. On the other hand, linear decay is defined by a constant rate of change, where the original value is decreased by the same amount at each time interval. In other words, exponential decay is non-linear, while linear decay is a linear function. Therefore, it is important to understand the difference between these two types of decay to accurately model and predict the decrease in value over time in various scenarios.
The Difference Between Exponential Growth and Linear Growth
Exponential growth and linear growth are two different ways in which populations or quantities can increase over time. Linear growth is a steady increase by a fixed amount over equal intervals of time. For example, if a population grows by 100 individuals per year, then the increase each year will remain constant. On the other hand, exponential growth occurs when a population or quantity increases at a constant percentage or factor over equal intervals of time. This means that the rate of growth itself is increasing over time, resulting in a rapid increase in population or quantity. For example, if a population doubles each year, then the growth rate will be 100% in the first year, 200% in the second year, and so on. the main difference btween exponential and linear growth is the way in which the growth rate changes over time, with linear growth being steady and exponential growth increasing rapidly.
Identifying Linear and Exponential Word Problems
When analyzing a word problem, you can determine whether it is a linear or exponential function by examining the way in which the growth or decay is expressed. If the problem involves an increase or decrease by a fixed value, such as a rate or constant amount, then it is likely a linear function. In this case, the equation will have the form y = mx + b or f(x) = (rate) x + (starting amount).
On the other hand, if the problem involves growth or decay expressed through multiplication, such as doubling or halving, then it is likely an exponential function. In this case, the equation will have the form y = ab^x or f(x) = (initial amount) * (growth or decay rate)^x.
It is important to carefully read and understand the problem in order to determine which type of function to use. By identifying the type of function, you can better solve the problem and understand the relationship beteen the variables.
Identifying Linear and Exponential Patterns
To determine whether a pattern is linear or exponential, you need to observe the relationship between the values in the pattern. In a linear pattern, the values increase or decrease by the same amount with each successive term. For example, the pattern 1, 3, 5, 7, 9… is linear, because each term increases by 2.
In contrast, in an exponential pattern, the values increase or decrease by the same percent with each successive term. For example, the pattern 2, 4, 8, 16, 32… is exponential, because each term is twice the previous term.
To furthr distinguish between linear and exponential patterns, you can plot the values on a graph. If the resulting graph shows a straight line, the pattern is linear. If the graph shows a curve that increases or decreases at a faster rate over time, the pattern is exponential.
In summary, to determine if a pattern is linear or exponential, you need to observe the relationship between successive terms, plot the values on a graph, and analyze the resulting curve.
Is Exponential Growth Faster Than Linear Growth?
Exponential growth is faster than linear growth. In linear growth, the change occurs at a constant rate, while in exponential growth, the change is multiplied during each time period. This means that with exponential growth, the rate of change increases rapidly over time. For instance, if a population grows at a linear rate of 1% per year, it would take 70 years to double. However, if the population grows at an exponential rate of 2% per year, it would only take 35 years to double. Therefore, exponential growth is much faster than linear growth.

Source: slideplayer.com
The Growth of Humans: Linear or Exponential?
Human growth is considered exponential rther than linear. This means that the rate of growth is increasing over time. The world’s population has increased from 2.5 billion in 1950 to over 7.7 billion in 2019, and is projected to reach 9.7 billion by 2050. This exponential growth can be attributed to various factors, such as advances in medical science, increased agricultural productivity, and improved standards of living. As the population continues to grow, it puts a strain on natural resources and raises concerns about sustainability for future generations. It is important to understand the implications of exponential population growth and work towards finding solutions to mitigate its negative effects.
Explaining Linear Growth
Linear growth refers to the phenomenon wherein a particular quantity or variable grows at a constant rate over time. In other words, if a quantity is increasing linearly, the amount it increases by is the same for every unit of time. For example, if a company’s revenue increases by $1000 every month, then it is experiencing linear growth.
Linear growth can be visualized as a straight line on a graph, where the y-axis represents the quantity being measured and the x-axis represents time. If the line is straight and sloping upwards at a constant rate, then the growth is linear.
It is important to note that linear growth is different from exponential or logarithmic growth, where the rate of growth increases or decreases over time. Linear growth is a simpler and more predictable pattern of growth, whih makes it easier to forecast future values and trends.
Identifying Exponential Data
To determine whether data is exponential, we need to look for a specific pattern in the relationship between the independent and dependent variables. Specifically, we need to examine whether the ratio between values of the dependent variable remains constant as we increase the independent variable by a fixed amount.
One way to check for this pattern is to plot the data on a graph and examine the shape of the curve. An exponential function will show a curve that initially rises slowly and then increases more rapidly, creating a characteristic J-shape curve.
Another way to check for an exponential pattern is to calculate the ratio of the dependent variable between two consecutive values of the independent variable. If this ratio is the same for evey pair of consecutive values, then the function is exponential. This can be expressed mathematically as y/x = k, where y is the dependent variable, x is the independent variable, and k is a constant ratio.
In summary, to identify exponential functions, we need to look for a consistent ratio between values of the dependent variable as we increase the independent variable by a fixed amount. Whether we examine the graph or calculate the ratio mathematically, the key is to identify the characteristic J-shape curve that is indicative of an exponential relationship.
Identifying the Type of Function
To determine whether a function is linear, quadratic or exponential, you need to analyze its behavior based on the changes in the independent variable, or input values.
Linear functions have a constant rate of change or slope and can be represented by a straight line on a graph. To check for linearity, you can plot the points and see if they fall alng a straight line. Alternatively, you can calculate the slope using the formula (change in y)/(change in x), and if the slope is constant, the function is linear.
Quadratic functions have a degree of 2 and can be represented by a curved line on a graph called a parabola. To check for quadratic behavior, you can plot the points and see if they fall along a curve or parabola. Alternatively, you can calculate the second differences between the y-values and if these differences are constant, the function is quadratic.
Exponential functions have a constant ratio between the output and input values, and can be represented by a curved line that increases or decreases rapidly. To check for exponential behavior, you can plot the points and see if they follow a curve that increases or decreases rapidly. Alternatively, you can calculate the ratio between the y-values and if this ratio is constant, the function is exponential.
The behavior of a function can be determined by analyzing the changes in the independent variable and comparing them to the expected behavior of linear, quadratic, or exponential functions.
Identifying Linear Expressions
A linear expression is one where the highest power of the variable involved is 1. In oter words, if the expression can be written in the form ax + b, where a and b are constants, then it is a linear expression. When graphed, a linear expression will form a straight line. Therefore, if the graph of an equation appears as a straight line, it is a linear equation, and the expression can be classified as linear. On the other hand, if the graph of an equation takes the shape of a curve or a non-linear shape, it is not a linear equation. It is important to note that a linear expression can have more than one variable, as long as the highest power of any variable involved is 1.
Conclusion
Understanding the difference between exponential and linear functions is crucial in solving real-world problems. The key difference lies in the way they change over time. Linear functions change by a constant amount, while exponential functions change by a constant percentage or factor. This means that exponential decay or growth can result in dramatic changes over time, whereas linear decay or growth will result in a more gradual change. It’s important to correctly identify which type of function is appropriate for the given situation. By doig so, we can make informed decisions and accurately predict future outcomes. Whether it’s calculating population growth, predicting the depreciation of an asset, or analyzing trends in data, understanding the difference between exponential and linear functions is a valuable skill in many fields.
