Triangles are fundamental shapes in geometry, and they have a wide range of applications in various fields. One of the most interesting types of triangles is the equilateral right triangle. This shape is unique in that it combines the properties of both an equilateral triangle and a right triangle. In this blog post, we will explore the properties of an equilateral right triangle and its applications.
An equilateral right triangle, as the name suggests, is a triangle that is both equilateral and right-angled. This means that all three sides of the triangle are equal in length, and one of the angles is a right angle (90 degrees). Since an equilateral triangle has angles of 60 degrees each, the other two angles in the equilateral right triangle are also 60 degrees. Therefore, an equilateral right triangle is also an equiangular triangle.
The Pythagorean Theorem states that in a right triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides. In an equilateral right triangle, all three sides are equal, so we can express this theorem as:
A^2 + a^2 = c^2
Where a is the length of one of the legs (the shorter sides), and c is the length of the hypotenuse.
We can simplify this equation to:
2a^2 = c^2
Therefore, in an equilateral right triangle, the length of the hypotenuse is equal to the square root of 2 times the length of one of the legs. This relationship between the sides of an equilateral right triangle is useful in various applications.
The unique properties of an equilateral right triangle make it useful in various fields, including mathematics, engineering, and physics. Here are some applications of an equilateral right triangle:
– In trigonometry, the ratios of the sides of a right triangle are used to calculate angles and distances. The properties of an equilateral right triangle can be used to derive trigonometric identities and formulas.
– In engineering, equilateral right triangles are useful in the design of structures that require precise angles and measurements. For example, the corners of a square can be constructed using two equilateral right triangles, which ensures that the angles are exactly 90 degrees.
– In physics, equilateral right triangles can be used to calculate the components of a vector (a quantity with both magnitude and direction). The legs of the triangle represent the x and y components of the vector, and the hypotenuse represents the magnitude of the vector.
An equilateral right triangle is a unique and intriguing shape that combines the properties of both an equilateral triangle and a right triangle. Its properties and applications make it useful in various fields, including mathematics, engineering, and physics. Understanding the properties of an equilateral right triangle can help us solve problems and design structures with precision and accuracy.
Can an Equilateral Right Triangle Exist?
There is no equilateral right triangle. An equilateral triangle has all three angles equal to 60 degrees. On the other hand, a right triangle has one angle equal to 90 degrees. It is not possible to have both 60 degrees and 90 degrees as angles in a triangle. Therefore, an equilateral triangle cannot be a right triangle. In fact, the only way to have a right triangle is to have one angle equal to 90 degrees and the other two angles must be acute angles (less than 90 degrees).

Source: youtube.com
Can a Right Triangle Be Equiangular?
A right triangle cannot be equiangular. An equiangular triangle is a triangle in which all three interior angles are equal to each other and each angle measures 60°. However, in a right triangle, one of the angles is a right angle, which measures 90°. Therefore, the other two angles must add up to 90° in order to satisfy the angle sum property of a triangle, making them unequal to each other. Hence, a right triangle cannot be equiangular as it has one angle that is not equal to the other two angles.
Identifying an Equilateral Triangle
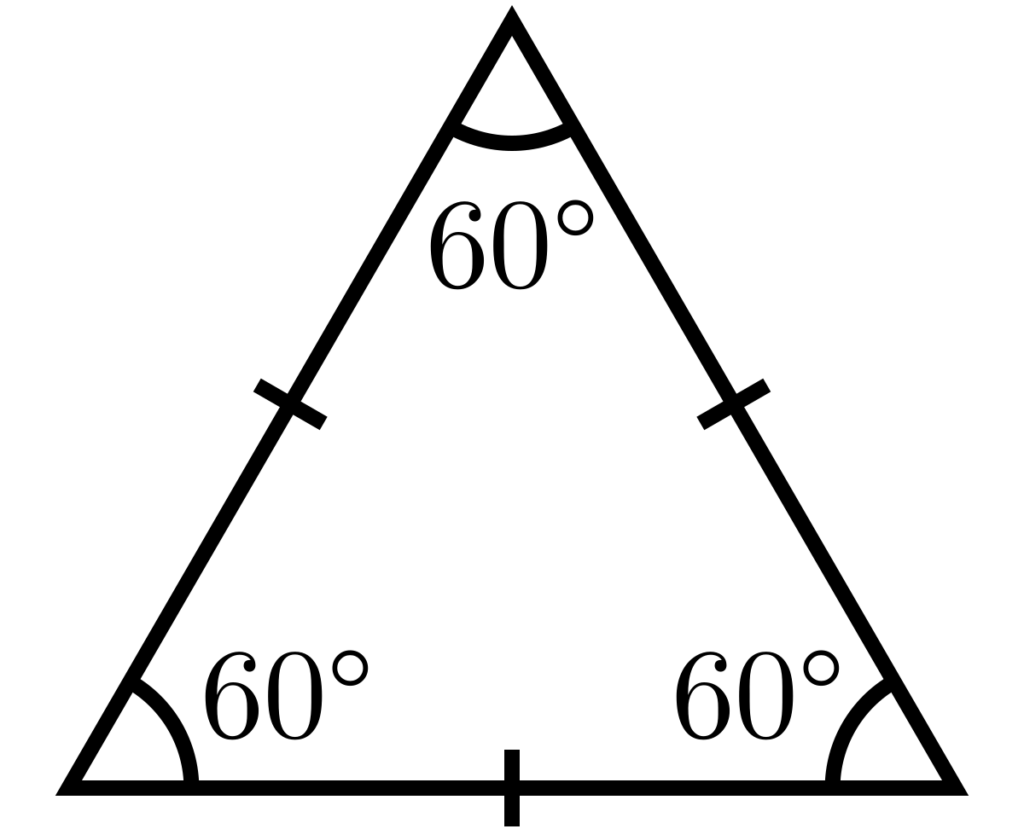
A triangle is considered equilateral if and only if all three sides of the triangle are of equal length. Therefore, in order to determine if a triangle is equilateral, one must measure all three sides and compare their lengths. Another way to identify an equilateral triangle is to examine its angles. Since all three sides are of equal length, all three angles will also be equal in measure, each measuring 60 degrees. It is important to note that if only two sides are equal in length, the triangle is not equilateral, but rather isosceles. to identify an equilateral triangle, one must ensure that all three sides are of equal length and all three angles are of equal measure.
Are the Sides of an Equilateral Triangle Equal?
All three sides of an equilateral triangle are equal in length. This is because the prefix “equi” means “equal,” and “lateral” refers to the sides of the triangle. Therefore, an equilateral triangle has three equal sides.
The Properties of an Equilateral Triangle
An equilateral triangle is called a regular polygon with three sides equal, meaning all three sides of the triangle are equivalent in length. The term “equilateral” is derived from the Latin words “aequus” and “latus,” wich mean “equal” and “side,” respectively. Therefore, the word “equilateral” simply refers to the fact that all sides of the triangle are equal in length. An equilateral triangle has some unique properties that distinguish it from other types of triangles, such as having three congruent angles that each measure 60 degrees. an equilateral triangle is a fundamental shape in geometry and is used in various mathematical and scientific applications.
Can a Right Triangle Have Two Equal Sides?
A right triangle can have two equal sides. Such a triangle is called an isosceles right triangle. In an isosceles right triangle, the two legs are equal in length, and the hypotenuse is the square root of 2 times the length of each leg. The two acute angles in an isosceles right triangle are also congruent, measuring 45 degrees each.
Can a 90 Degree Angle Be Equilateral?
A 90 degree angle cannot be equilateral. An equilateral triangle has all three angles equal to 60 degrees and all three sides of equal length. A 90 degree angle is a right angle, and it is only found in a right triangle. In a right triangle, one angle is 90 degrees, but the other two angles are not equal. Therefore, a triangle with a 90 degree angle cannot be equilateral, as it does not meet the requirements of having equal angles and sides.
Impossibility of Drawing a Right Equilateral Triangle
An equilateral triangle is a triangle with three equal sides and three equal angles. The longest side theorem states that in a triangle, the longest side is across the largest angle. Since all the sides of an equilateral triangle are equal, the angles must also be equal. In oter words, each angle in an equilateral triangle measures 60 degrees.
A right triangle, on the other hand, is a triangle with one angle measuring 90 degrees. It can be proved mathematically that the sum of the angles of a triangle is always 180 degrees. Therefore, in a right triangle, the other two angles must add up to 90 degrees. Since each angle in an equilateral triangle measures 60 degrees, it is impossible to have an angle measuring 90 degrees in an equilateral triangle. Therefore, it is impossible to draw a right equilateral triangle.
Are All Triangles with Equal Sides Equal Angles?
All equilateral triangles have three equal angles, each measuring 60 degrees. This is because an equilateral triangle is defined as a triangle in which all three sides are congruent, and the angles opposite to these sides are also congruent. The sum of the interior angles of a triangle is always 180 degrees, so in an equilateral triangle, each angle must measure 60 degrees to add up to 180 degrees. Therefore, the answer to the question “Are all equilateral triangles 60?” is yes.
Conclusion
An equilateral right triangle is a geometrical impossibility. This is because an equilateral triangle by definition has three equal angles of 60 degrees each, making the sum of the interior angles 180 degrees. On the othr hand, a right triangle has one interior angle of 90 degrees, leaving only 90 degrees for the other two angles. It is clear, therefore, that it is impossible for an equilateral triangle to also be a right triangle.
While equilateral triangles are always acute-angled triangles with angles measuring 60 degrees, right triangles have one angle that measures 90 degrees. Equilateral triangles have sides of equal length, while right triangles have one side that is perpendicular to the other two sides.
Although an equilateral right triangle does not exist, understanding the properties of both equilateral and right triangles can help us better understand the concepts of geometry and mathematics.
