Springs are ubiquitous in our daily lives, from the suspension systems in our cars to the mattress we sleep on. They are used to store and release energy in a variety of applications. The amount of force a spring exerts per unit of displacement is known as its spring constant. The question arises, does the spring constant change? Let’s explore this in more detail.
Firstly, it’s important to understand what the spring constant is and how it’s determined. The spring constant (k) is a measure of a spring’s stiffness and is defined as the force required to stretch or compress the spring by a unit of length. In other words, it’s the ratio of the force applied to the displacement produced. The unit of measurement for spring constant is Newtons per meter (N/m).
Now, let’s answer the question of whethr the spring constant changes. The answer is both yes and no, depending on the situation. In general, the spring constant of a particular spring remains constant as long as the material is elastic. This means that the spring will return to its original shape and size after being stretched or compressed. However, if the material is stretched beyond its elastic limit, it will become permanently deformed, and the spring constant will change.
Furthermore, the spring constant can also change due to other factors such as temperature, stress, and strain. For instance, if a spring is exposed to high temperatures, it may lose its elasticity and become softer, leading to a decrease in its spring constant. Similarly, if a spring is subjected to high stress or strain, it may undergo plastic deformation, resulting in a change in its spring constant.
Moreover, the spring constant can also vary depending on the design and manufacturing process of the spring. The thickness and diameter of the wire used to make the spring, the number of turns per unit length, and the overall length of the spring can all affect its spring constant. A thicker wire and more turns will result in a stiffer spring with a higher spring constant.
The spring constant of a spring can change depending on various factors such as material, temperature, stress, strain, and design. However, in general, the spring constant remains constant as long as the material is elastic and not subjected to any external factors that may alter its properties. Understanding the behavior of springs and their spring constants is critical in many applications, from designing suspension systems to manufacturing precision instruments.
Does the Spring Constant Remain Constant?
The spring constant remains constant as long as the material is elastic. The spring constant is a property of the spring itself, and it represents the force required to stretch or compress the spring by a cetain distance. Mathematically, the spring constant (k) is defined as the ratio of the force applied (F) to the displacement produced (x), or k = F/x. This relationship is known as Hooke’s Law, and it only holds true for elastic materials, which can return to their original shape after deformation. If the material reaches its elastic limit, it will no longer obey Hooke’s Law and the spring constant will no longer remain constant.
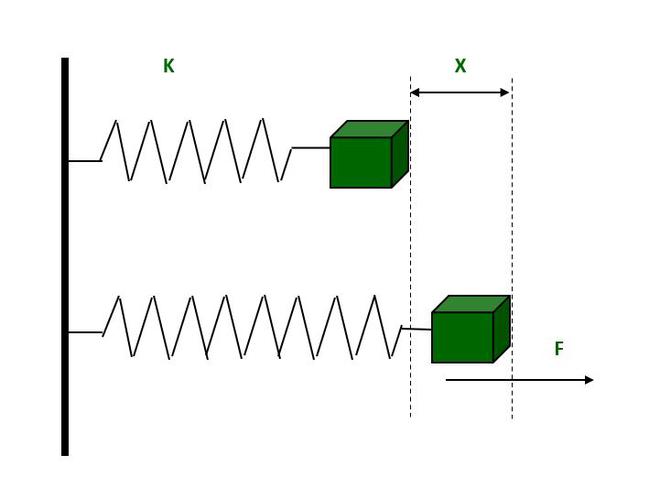
Does the K Value of a Spring Vary?
The k value of a spring, also known as the spring constant, is a characteristic property of the spring that represents its stiffness. The k value is defined as the ratio of the force applied to the spring to the displacement it experiences. According to Hooke’s law, the displacement of a spring is directly proportional to the force applied to it, as long as the limit of proportionality is not exceeded. Therefore, the k value of a spring is a constant value that depends on the material, shape, and dimensions of the spring.
In ideal conditions, the k value of a spring should not change, meaning that the spring should obey Hooke’s law and maintain a linear relationship between force and displacement. However, in real-world situations, the k value of a spring may change due to various factors such as wear and tear, deformation, temperature changes, and material fatigue. For example, if a spring is subjected to excessive force or deformation, it may exceed its limit of proportionality and become permanently deformed, leading to a change in its k value. Similarly, if a spring is exposed to high temperatures or corrosive environments, its material properties may change, affecting its k value.
Therefore, whie the k value of a spring is generally considered to be a constant property, it is important to note that it may change under certain conditions. Proper maintenance, handling, and storage of the spring can help minimize any changes in its k value and ensure its reliable performance over time.
Does Changing Force Affect Spring Constant?
The force by itself does not change the spring constant. The spring constant is a physical property of the spring, whch is determined by the material and dimensions of the spring. However, the spring constant can be changed by altering the physical properties of the spring, such as its length, cross-sectional area, or the material it is made of. Applying a force to a spring can cause it to deform, and if the deformation is significant, it can affect the spring constant. However, this is generally considered to be a temporary change, and the spring will return to its original spring constant once the force is removed. Therefore, while force can affect the behavior of a spring, it does not directly change its spring constant.
How Does the Spring Constant K Vary?
The spring constant, denoted by the symbol k, is a measure of the stiffness of a spring. It represents the force required to stretch or compress the spring by a given amount. The spring constant depends on several factors, including the material from which the spring is made, the thickness of the wire used to make the spring, the diameter of the turns of the coil, the number of turns per unit length, and the overall length of the spring.
The stiffness of the spring material is a crucial factor in determining the spring constant. Different materials have different stiffnesses, and the spring constant will be higher for stiffer materials. The thickness of the wire used to make the spring is also important, as thicker wires will produce stiffer springs with higher spring constants.
The diameter of the turns of the coil is another factor that affects the spring constant. Larger diameters will result in a lower spring constant, wile smaller diameters will produce a higher spring constant. The number of turns per unit length is also significant, as more turns will result in a stiffer spring with a higher spring constant.
The overall length of the spring is a factor that affects the spring constant. Longer springs will be less stiff and have a lower spring constant, while shorter springs will be stiffer and have a higher spring constant.
The spring constant depends on the material, wire thickness, coil diameter, number of turns, and overall length of the spring. These factors all contribute to the stiffness of the spring and determine the amount of force required to stretch or compress it.
The Constant Nature of Spring Constant
The spring constant, also known as the force constant, is a physical property of a spring that determines how much force is required to stretch or compress it by a certain amount. The reason why the spring constant stays the same is because it is a characteristic of the spring itself, and it is determined by its material and geometry.
When a spring is stretched or compressed, it exerts a force that is proportional to the displacement from its equilibrium position. This relationship is described by Hooke’s law, which states that the force is equal to the spring constant multiplied by the displacement. Therefore, if the spring constant were to change, the force exerted by the spring would also change, and Hooke’s law would no longer hold.
Furthermore, the spring constant is determined by the stiffness of the material the spring is made of, as well as its geometry (such as the diameter of the wire and the number of coils). These factors are intrinsic to the spring and do not change uness the spring is physically altered. Therefore, the spring constant remains constant as long as the spring is not damaged or deformed in any way.
The spring constant stays the same because it is a fundamental property of the spring that is determined by its material and geometry, and it is not influenced by external factors such as the amount of force applied to the spring.

Does the Spring Constant Value Vary Across Different Springs?
The spring constant value is not the same for eery spring. The spring constant, also known as the force constant or stiffness coefficient, is a property of an individual spring that depends on its material, shape, and size. A spring made of a stiffer material, like steel, will have a higher spring constant than a spring made of a less stiff material, like rubber. Similarly, a spring with a larger cross-sectional area or a smaller length will be stiffer and have a higher spring constant than a spring with a smaller cross-sectional area or a larger length. Therefore, the spring constant value varies from spring to spring and is unique to each spring. It is an important parameter to consider when designing and using springs in various applications.
Effects of Changes on K Value
The K value, or equilibrium constant, is a measure of the extent to which a chemical reaction reaches equilibrium. The value of K is determined by the ratio of the concentrations of products to the concentrations of reactants, each raised to their respective stoichiometric coefficients. The K value is dependent on the temperature, pressure, and concentrations of the reactants and products.
The temperature has a significant effect on the K value. For an endothermic reaction, increasing the temperature increases the kinetic energy of the molecules, which results in greater activation energy beng overcome and a higher concentration of products. Therefore, the K value increases with an increase in temperature. On the other hand, when the temperature is decreased, the kinetic energy of the molecules decreases, which results in a lower concentration of products. Hence, the K value decreases with a decrease in temperature.
For an exothermic reaction, increasing the temperature leads to a decrease in the concentration of products, as the excess heat energy is absorbed by the reactants, causing the equilibrium to shift towards the reactants side. Therefore, the K value decreases with an increase in temperature. Conversely, decreasing the temperature leads to an increase in the concentration of products, causing the equilibrium to shift towards the products side. Thus, the K value increases with a decrease in temperature.
The K value changes with changes in temperature, pressure, and concentrations of the reactants and products. However, the temperature is one of the most significant factors that affect the K value.
Can the K Value be Altered?
The vale of K can change. K, also known as the rate constant, is dependent on various factors such as temperature, concentration, and the nature of the reactants. In particular, changes in temperature can have a significant impact on the value of K. This is because temperature affects the rate of chemical reactions, and thus the rate constant. As the temperature changes, the area exposed to the reaction may also change, which can further alter the value of K. Additionally, changes in the concentration of reactants and the nature of the reactants themselves can also affect the value of K. K is not a fixed value, but rather a variable that depends on a range of factors.
Factors That Affect the Value of K
The value of K, also known as the equilibrium constant, is determined solely by temperature and is independent of the pressure, concentration of reactants/products, and the presence of a catalyst. This means that changes in the pressure, concentration or addition of a catalyst do not impact the value of K. However, it is important to note that changes in temperature can significantly alter the value of K. As temperature increases, the value of K may increase or decrease, depending on the reaction. In general, for exothermic reactions, an increase in temperature leads to a decrease in the value of K, while for endothermic reactions, an increase in temperature leads to an increase in the value of K. Other factors that can affect the value of K include changes in the reaction stoichiometry, which can result in a change in the equilibrium concentration of reactants and products, and changes in the overall reaction conditions, such as the presence of other reactants, solvents, or catalysts. It is important to understand thee factors when studying chemical equilibria and their associated equilibrium constants.

The Relationship Between Spring Constant and Gravity
The spring constant does not depend on gravity. The spring constant, denoted by the symbol k, is a measure of the stiffness of a spring and is defined as the force per unit displacement required to stretch or compress the spring. It only depends on the material used to make the spring and the shape or geometry of the spring.
Gravity, on the other hand, is a force that attracts objects towards each other. It affects the net force on the spring but does not have any impact on the spring constant. This means that the spring constant remains constant reardless of the presence or absence of gravity.
To put it simply, the spring constant is an inherent property of the spring that remains constant irrespective of the external factors such as gravity. Therefore, it is safe to conclude that the spring constant is independent of gravity.
The Relationship Between Spring Constant and Mass
The spring constant is a physical property of a spring that represents the amount of force required to stretch or compress the spring by a certin length. It is typically denoted by the symbol ‘k’ and is measured in units of force per unit length.
Contrary to what one might expect, the spring constant does not depend on the mass of the object attached to it. This is because the spring constant is a property of the spring itself, and is determined by factors such as the material it is made of, its shape, and its dimensions.
However, the mass of the object attached to the spring can affect the behavior of the system as a whole. Specifically, the period of oscillation of a mass-spring system (i.e., the time it takes for the object to complete one full cycle of motion) depends on both the spring constant and the mass of the object. This is given by the equation T = 2π√(m/k), where T is the period, m is the mass, and k is the spring constant.
While the spring constant itself does not depend on the mass of the object, the mass can affect how the system as a whole behaves.
The Relationship Between Spring Constant and Force
The spring constant is directly proportional to force. This means that the amount of force required to stretch or compress a spring-like object is directly rlated to its spring constant. The spring constant, also known as the stiffness constant, is a measure of how much force is required to produce a certain amount of deformation in the spring. The higher the spring constant, the more force is needed to stretch or compress the spring by a certain amount. This relationship is expressed mathematically as F = kx, where F is the force applied, k is the spring constant, and x is the displacement or deformation of the spring. Therefore, if the spring constant increases, the force required to stretch or compress the spring will also increase in direct proportion to the constant.
The Impact of Temperature on Spring Constant
The spring constant is a measure of how stiff a spring is, and it is typically defined as the amount of force required to stretch or compress the spring by a certin amount. However, the spring constant can change with temperature due to microstructural effects.
At higher temperatures, the atoms in the spring begin to vibrate more rapidly, which can cause the bonds between them to weaken and become more flexible. As a result, the spring becomes less stiff and its spring constant decreases. Conversely, at lower temperatures, the atoms in the spring vibrate less and the bonds between them become stronger, making the spring stiffer and its spring constant higher.
Additionally, some materials may undergo phase changes at certain temperatures, which can also affect their spring constant. For example, if a material transitions from a crystalline to an amorphous structure, its spring constant may change significantly.
Therefore, it is important to account for the effects of temperature on the spring constant when measuring and analyzing the behavior of springs or other elastic materials.

Source: edrawmax.com
The Effects of Increasing Spring Constant K
When the spring constant k is increased, the spring becomes stiffer and more resistant to stretching. This means that a greater force is required to stretch the spring by a certain amount. As a result, the oscillation frequency of a mass attached to the spring also increases. In other words, the mass will be able to move back and forth more quickly than before. This is because the period of oscillation is inversely proportional to the square root of the spring constant. So, as the spring constant increases, the period decreases. This relationship is decribed by Hooke’s Law, which states that the force exerted by a spring is directly proportional to its spring constant and the distance it is stretched or compressed. Therefore, increasing the spring constant k will lead to a stronger and faster oscillation of the mass attached to the spring.
The Invariability of Spring Constant with Mass
The spring constant is a property of the spring itself and it represents the stiffness of the spring. It is defined as the force required to stretch or compress a spring by a crtain distance. The spring constant is determined by the material properties of the spring, such as the Young’s modulus and the cross-sectional area of the wire used to make the spring.
The mass of an object attached to a spring does not affect the spring constant because the force exerted by the spring depends only on the displacement of the spring from its equilibrium position. The displacement of the spring is determined by the difference between the length of the spring with the mass attached and its original length without the mass. Therefore, the force exerted by the spring is proportional to the displacement, not the mass.
In other words, the spring constant is a measure of the spring’s ability to resist deformation and is independent of the mass attached to it. This means that a spring with a higher spring constant will be stiffer and require more force to be stretched or compressed than a spring with a lower spring constant, regardless of the mass attached to it.
Conclusion
The spring constant does not change for a given spring under constant conditions. This is beause the spring constant is a property of the spring itself, and is determined by factors such as the stiffness of the spring material and the number of turns per unit length. However, it is important to note that Hooke’s Law only remains true when the material is elastic. The stiffer the spring, the less change in displacement it will experience as a weight of certain magnitude is added to the end of the spring, resulting in a higher spring constant. Conversely, a less stiff spring will experience more displacement for the same weight, resulting in a lower spring constant. Therefore, while the spring constant may not change, it is influenced by the properties of the spring and the conditions under which it is used.
