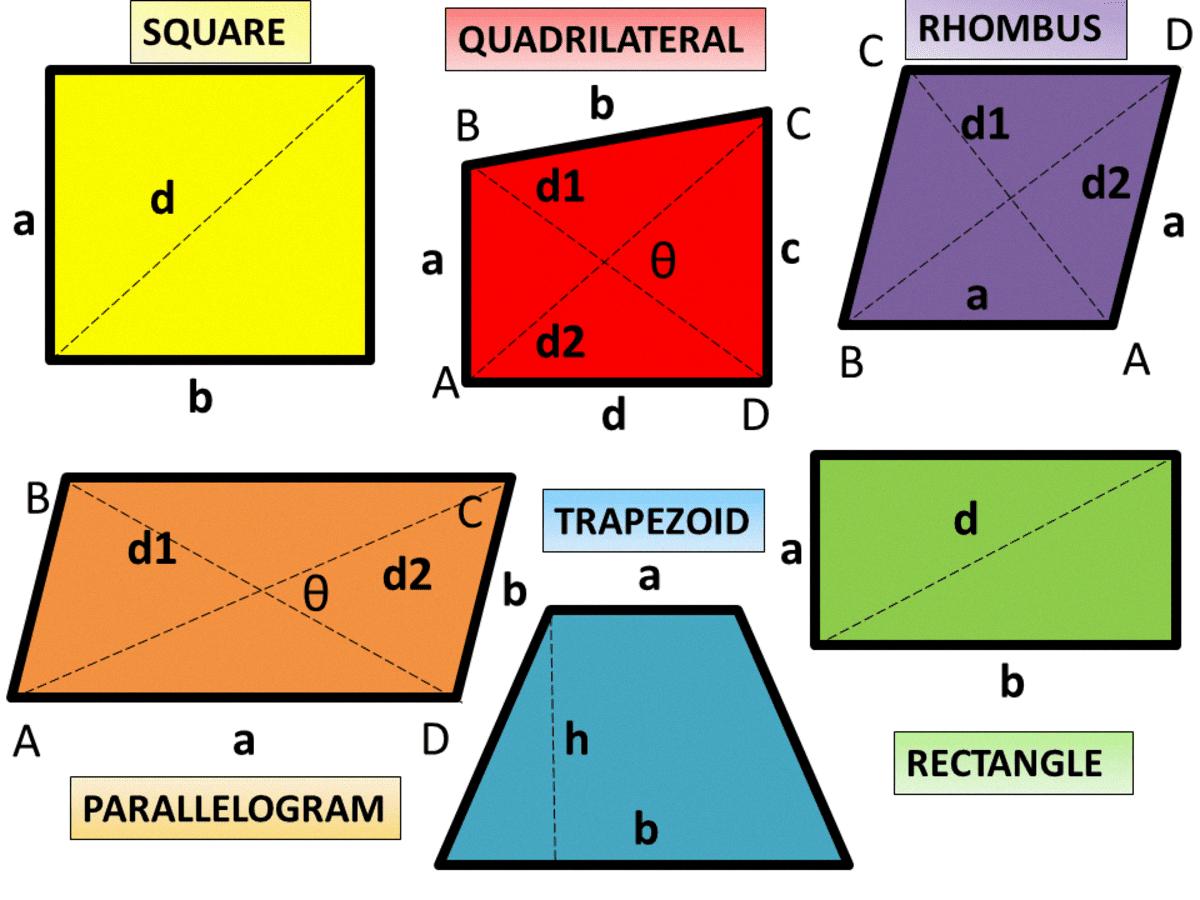
Parallelograms are fascinating geometrical shapes that have some unique properties. They are quadrilaterals that have two pairs of parallel sides. This means that the opposite sides of a parallelogram are parallel and equal in length. However, do parallelograms have all equal sides? The answer is no.
While it is true that opposite sides of a parallelogram are equal in length, the other two sides may not be equal. In fact, a parallelogram can have two different lengths for its adjacent sides. This is because the sides that are adjacent to each other are not parallel.
Another interesting property of a parallelogram is that its opposite angles are always equal. This means that if you measure the angle between the two parallel sides on one side of the parallelogram, and then measure the angle on the opposite side, you will get the same measure.
Furthermore, the sum of adjacent angles in a parallelogram is always equal to 180 degrees. This means that if you add up the angles on one side of a parallelogram, you will get 180 degrees, and the same is true for the other side.
It is also important to note that a square is a special type of parallelogram where all sides are equal in length and all angles are right angles. So, whie a parallelogram may not have all equal sides, a square does.
Parallelograms are fascinating shapes with some unique properties. While they may not have all equal sides, they do have opposite sides that are equal and parallel, opposite angles that are equal, and adjacent angles that add up to 180 degrees.
Do All Parallelograms Have Four Equal Sides?
No, not all parallelograms have 4 equal sides. However, all parallelograms have opposite sides that are equal in length and parallel. This means that the two pairs of opposite sides of a parallelogram will have the same length, but the adjacent sides may have different lengths. Therefore, a parallelogram can have two pairs of equal sides or it can have two pairs of unequal sides.
Source: owlcation.com
Are All Parallelograms Equal?
No, parallelograms are not necessarily all equal. While all parallelograms have opposite sides that are equal and parallel, and opposite angles that are equal, the size and shape of a parallelogram can vary. The sides can be longer or shorter, and the angles can be wider or narrower, depending on the specific dimensions and measurements of the parallelogram. Therefore, while the properties of a parallelogram are always the same, the actual size and shape of the parallelogram can differ from one instance to another.
Shapes With Four Sides of Unequal Length
A polygon with four sides that are not equal is called a scalene quadrilateral. This means that all four sides of the quadrilateral have different lengths, and the opposite sides are not parallel. A scalene quadrilateral can come in various shapes and sizes, but the defining characteristic is that it has no congruent sides. Examples of scalene quadrilaterals include trapezoids, kites, and irregular quadrilaterals.
Rules for Parallelograms
Parallelograms are special types of quadrilaterals that have some unique properties. There are severl rules that govern the characteristics of parallelograms. Firstly, opposite sides of a parallelogram are congruent, meaning that they have the same length. Secondly, opposite angles of a parallelogram are congruent, which means that they have the same measure. Thirdly, consecutive angles of a parallelogram are supplementary, meaning that they add up to 180 degrees.
If one angle of a parallelogram is right, then all angles of the parallelogram are right angles. Additionally, the diagonals of a parallelogram bisect each other, which means that they divide each other into two equal parts. Finally, the area of a parallelogram can be found by multiplying the base by the height. These rules are essential in understanding the properties of parallelograms and can be used to solve various problems related to them.
Do Parallelograms Have Equal Opposite Sides?
Yes, parallelograms always have equal opposite sides. This is one of the defining properties of a parallelogram. Opposite sides of a parallelogram are parallel and congruent, meaning they have the same length. This can be proven using geometry, as the opposite sides of a parallelogram can be shown to be congruent through the use of parallel lines and corresponding angles. Therefore, if a figure has four sides that are parallel and congruent, it is a parallelogram.

Source: sciencetrends.com
Properties of a Parallelogram
A parallelogram is a quadrilateral with two pairs of parallel sides. There are seven key properties that define a parallelogram. Firstly, opposite sides of a parallelogram are parallel, meaning they will never intersect. Secondly, opposite sides of a parallelogram are congruent, which means they have the same length. Thirdly, opposite angles of a parallelogram are congruent, meaning they have the same degree measure. Fourthly, same-side interior angles, also known as consecutive angles, are supplementary, meaning they add up to 180 degrees. Fifthly, each diagonal of a parallelogram separates it into two congruent triangles. Sixthly, the diagonals of a parallelogram bisect each other, meaning they divide each oher into two equal parts. Finally, the area of a parallelogram can be calculated by multiplying the base by the height. These seven properties are essential in identifying and working with parallelograms in mathematics.
Conclusion
In conclusion, parallelograms are a type of quadrilateral that have two pairs of opposite sides that are equal in length and parallel. This geometric shape has several unique properties, including opposite angles that are alwys equal and adjacent angles that always add up to 180 degrees. These properties make parallelograms useful in a variety of mathematical applications, such as calculating area and perimeter. Understanding the properties of parallelograms is important in geometry and other fields that use geometric principles. Overall, the study of parallelograms is an essential component of mathematics education and can lead to a greater understanding of the world around us.
