Welcome to the blog post about Chi Square Test and whether it is two tailed or not.
The Chi-squared test, also known as the Pearson’s chi-squared test, is a statistical method used to determine wheter two variables are related. It is based on the chi-square statistic, which measures the degree of difference between observed and expected frequencies in one or more categories. The chi-square statistic is one-tailed so it is used to reject the independence hypothesis.
When loking at a 2×2 table, both a one-sided and a two-sided significance level can be displayed; however, chi-square tests are always right-tailed tests. If p ? ? then you reject the null hypothesis; if you fail to reject then you accept it. The ?2 and F tests are one sided tests because we never have negative values of ?2 and F.
The Chi-square test of independence checks whether two variables are likely to be related or not. We have counts for two categorical or nominal variables, and an idea that they might not be related. The test gies us a way to decide if our idea is plausible or not by measuring the degree of difference between observed and expected frequencies in one or more categories.
In conclusion, although chi square tests can come in different forms – such as one tailed or two tailed – they will always be right tailed in order to measure the degree of difference between observed and expected frequencies in one or more categories when wanting to determine whether two variables are related or not.
Two-Tailed or One-Tailed Nature of the Chi-Square Test
The chi-squared test is usually used to test for independence between two variables, and it is a one-tailed test. This means that when the data are analyzed, the null hypothesis of independence is tested againt a single alternative hypothesis (that the variables are not independent). This means that the test can only be used to reject the null hypothesis, not to accept it.
However, in some cases where only a 2×2 table of data is available, then both a one-sided and two-sided significance level can be calculated. In this case, the chi-squared statistic can be used to either reject or accept the null hypothesis.
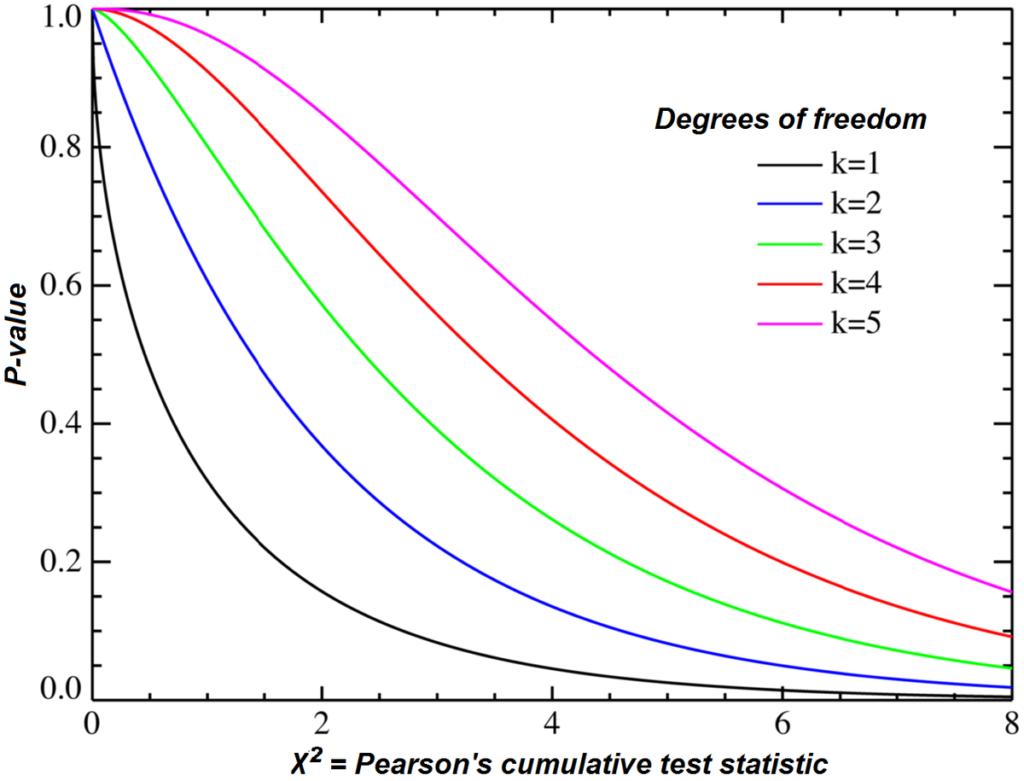
Is the Chi-Square Test Right-Tailed?
Yes, chi-square tests are right-tailed tests. This means that the test statistic is compared to a critical value for the right tail of a chi-square distribution. If the test statistic is greater than or equal to the critical value, then there is sufficient evidence to reject the null hypothesis. Conversely, if the test statistic is less than the critical value, then there is not enouh evidence to reject the null hypothesis.
The Use of One-Tailed Chi-Square Tests
Chi-square tests are one-tailed tests because the value of the test statistic, which is calculated using the difference between observed and expected counts, can only be positive. Since there are no negative values of chi-square, it is not possible to have a two-tailed test. The chi-square test statistic is calculated by summing the squared differences between observed and expected counts, divided by the expected count. This calculation produces a positive value, which can only result in a one-tailed test.
The Chi-Square 2 Way Test
A Chi-Square 2 Way Test is a statistical test used to examine the relationship between two categorical variables. This test is used to answer questions such as whether thee is an association between two variables, or whether differences exist between groups. The test measures the extent to which the observed frequencies of the two variables differ from what would be expected if there was no relationship between them. It does this by comparing observed counts of each combination of the two variables with expected counts, which are calculated from the marginal totals of those variables. If there is a significant difference between what is expected and what is observed, it can be concluded that an association exists between the variables. The Chi-Square 2 Way Test gives us a way to measure how likely it is for an association to exist based on our data.
Chi-Square Test Type
A Chi-square test is a type of hypothesis testing used to determine if there is a significant difference between the observed frequencies of two or more categorical variables. It uses the chi-square statistic, which measures how far the observed frequencies are from the expected frequencies. The chi-square statistic is calculated by summing up all of the squared differences between observed and expected values, then dividing by the expected values. The result is compared to a critical value from a chi-square table to determine whether or not it is statistically significant. For example, if you wanted to test whether there was a difference in the proportion of people who prefer cats versus dogs, you cold use a chi-square test.
Source: stats.stackexchange.com
Can a Chi-square Test Be Conducted with a Left-Tailed Distribution?
Yes, a chi-square test can be left-tailed. A left-tailed test is used to determine if the observed data is significantly lower than the expected data. To do this, you calculate the critical value of the chi-square statistic using the significance level and subtract it from 1. Then, you use that column in the chi-square table to find the left-tail critical value. If your observed statistic is less than this critical value, then you can reject the null hypothesis and conclude that there is a significant difference between the observed and expected data.
Two-Tailed Tests
A two-tailed test is a type of statistical test that is used to evaluate the likelihood of an observed result occurring due to random chance. This type of test assesses whether a sample differs significantly from a hypothesized population mean or another benchmark value. It does this by splitting the critical area of the distribution into two sides (tails) and testing whether the sample is greater or less than different ranges of values.
In order to perform a two-tailed test, researchers must first select an appropriate statistic for their analysis. Commonly used two-tailed tests include t-tests, chi-square tests, and z-tests. Once the appropriate statistic has been chosen, researchers then calculate a p-value which represents the probability that the observed result could have occurred due to random chance alone. If this p-value is less than the predetermined significance level (usually 0.05), then we can reject our null hypothesis and conclude that our sample differs significantly from the hypothesized population mean or benchmark value.
Overall, two-tailed tests are useful for determining if observed results differ significantly from what we expect to see in a population or benchmark value, and can povide valuable insight into research questions and hypotheses.
The Difference Between 1-Tailed and 2-Tailed Tests
A one-tailed test is a type of statistical hypothesis test in which the region of rejection for the null hypothesis is on one side of the sampling distribution. This means that the test is only looking for an effect in one direction (e.g. whether something is greater than or less than). For example, if we are testing to see if a certain drug has an effect on reaction time, we would use a one-tailed test because we are only expecting it to have an effect in one direction (i.e. making reaction time faster, not slower).
A two-tailed test, on the other hand, tests for an effect in both directions—whether something is greater than or less than. For example, if we were testing to see if a certain drug had an effect on weight gain, we would use a two-tailed test because it could either result in weight gain or loss.
The Benefits of Two-Tailed Tests
Two-tailed tests are better than one-tailed tests because they allow you to detect any differences between two means, regardless of the direction of the difference. This makes two-tailed tests more powerful and statistically valid than one-tailed tests. Additionally, two-tailed tests can provide more information about the relationship between the two means since both positive and negative differences are taken into account. By usig a two-tailed test, you can gain a better understanding of how two variables are related and how their values differ from one another.
When to Use a One-tailed Test
When determining whether to use a one-tailed test, it is important to consider the consequences of missing an effect in the untested direction. If the consequences are negligible and in no way unethical or irresponsible, then you can proceed with a one-tailed test. It is also important to consider the expected direction of the effect. If the expected direction of the effect is known and it would be irresponsible or unethical to miss an effect in that direction, then a one-tailed test should be used. Finally, if there is no expectation of an effect in eiter direction, then a two-tailed test should be used instead.
Different Types of Chi-Square Tests
The three types of Chi-square tests are the goodness of fit test, the test of independence, and the test for homogeneity.
The goodness of fit test is used to compare observed data with expected data to determine if they differ significantly. It is used to assess whether a sample matches a certain population or follows a specific distribution. For example, it can be used to assess whether a coin is fair or biased, or whether sample proportions match those expected in a population.
The test of independence is used to determine if two categorical variables are related. It can be used to compare different populations, such as gender and political party affiliation, or any two variables that are measured on a nominal scale (e.g., yes/no responses).
Finally, the test for homogeneity is used to determine if two or more samples were drawn from the same population. This test can help researchers identify differences betwen groups by examining how well their distributions match up. For example, it can be used to compare student grades between two classes to see if there are significant differences in performance between them.
Types of Chi-square Tests
The two most common types of chi-square tests are the Chi-square Test of Goodness of Fit and the Chi-square Test of Independence. The Chi-square Test of Goodness of Fit is used to determine if a sample data fits a theoretical distribution, while the Chi-square Test of Independence is used to test for relationships between two categorical variables. Both tests involve the comparison of observed frequencies to expected frequencies, and their results are evaluated using a chi-square statistic.
Comparing Two Variables with a Chi-Square 2×2 Test
A chi-square 2×2 test compares the frequency of two categorical variables within a single population. For example, it can be used to compare the number of males and females that responded with ‘yes’ to a particular question. It can also be used to compare the observed frequencies of two different variables (e.g. smoking status and age group) within a single population. The chi-square test evaluates whether or not these observed frequencies differ significantly from what would be expected if there were no relationship btween the two variables being tested. The result of this test is expressed in terms of a chi-square statistic, which is then compared to critical values from a chi-square distribution in order to determine if the difference between observed and expected frequencies is statistically significant.
Conclusion
The Chi-Square Test is a powerful tool for testing the independence of two categorical variables. It is a one-tailed test, meaning that it only tests if the data supports rejecting the null hypothesis that there is no relationship between the two variables. The test also provies a measure of how much evidence is present to reject this hypothesis. By comparing observed frequencies with expected values, we can understand how likely it is that two variables are associated. If there is strong evidence to support the rejection of the null hypothesis, then we can conclude that there is a relationship between the two variables.
