Percentile is a statistical measure that indicates a particular value in a data set below which a certain percentage of observations falls. It is a widely used concept in various fields such as education, healthcare, and finance. Percentiles are used to analyze data sets and determine how they compare to others in terms of distribution.
To calculate a percentile, you need to know the number of values in a data set, which should be sorted from smallest to largest. Let’s say we have a data set of 100 test scores, and we want to find the 75th percentile. The formula to find the ordinal rank of the 75th percentile is n = (P/100) x N. In this case, n = (75/100) x 100 = 75. This means that the 75th percentile is the value that is greater than or equal to 75 other values in the data set, and lower than or equal to 25 values.
However, if you want to find the value in the data set that corresponds to a particular percentile, you need to use a different formula. This formula involves the mean and standard deviation of the data set, as well as the z-score associatd with the desired percentile.
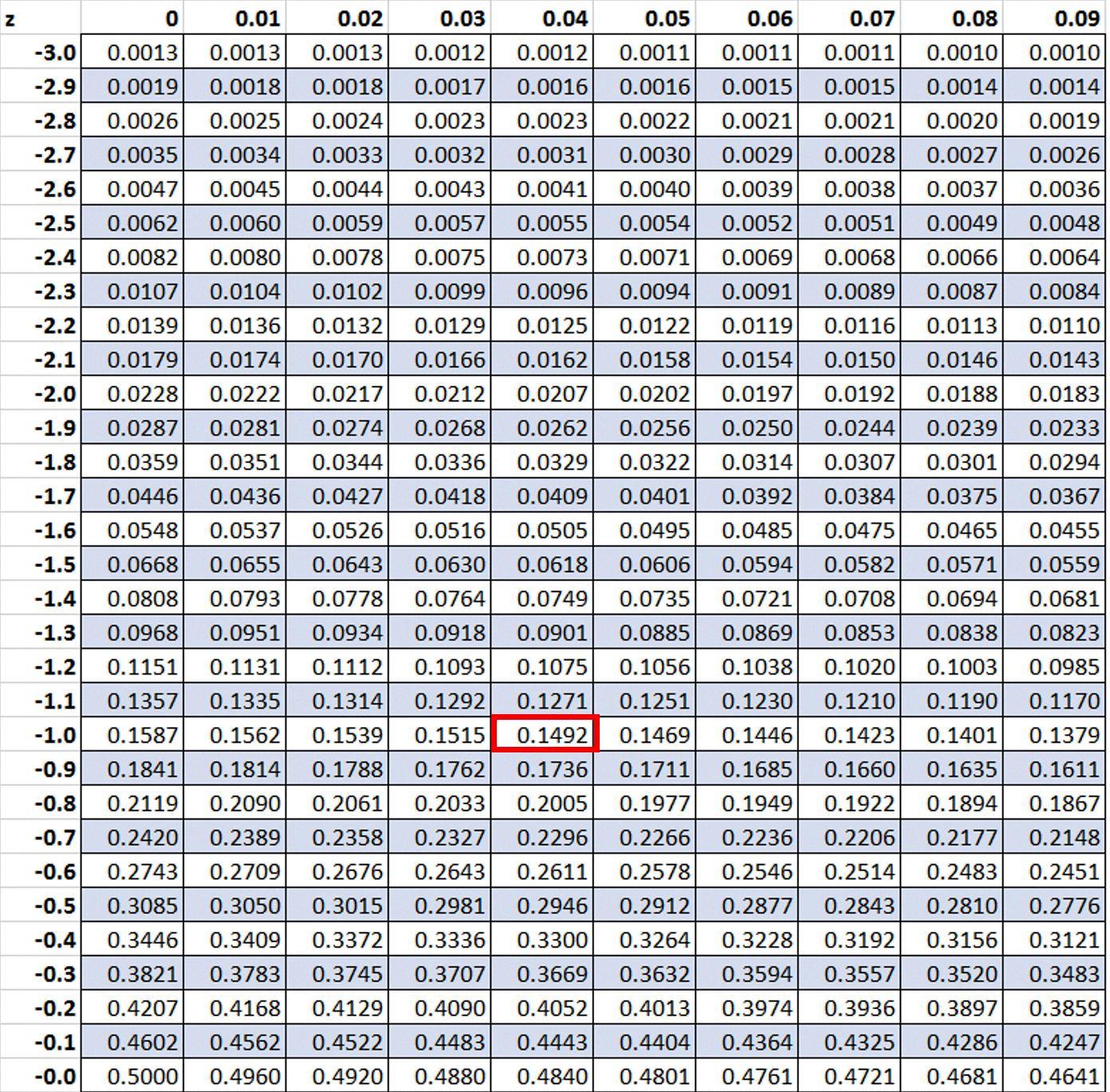
The formula to find the value at a certain percentile is X = μ + Zσ, where X is the value at the desired percentile, μ is the mean of the data set, σ is the standard deviation of the data set, and Z is the z-score associated with the desired percentile. The z-score can be found using a standard normal distribution table.
For example, let’s say we have a data set of 100 test scores, and we want to find the value at the 90th percentile. The mean of the data set is 75, and the standard deviation is 10. To find the z-score associated with the 90th percentile, we look up 0.900 in the standard normal distribution table, which gives us a z-score of 1.28. We then use the formula X = 75 + 1.28 x 10 = 88.8. This means that the value at the 90th percentile is 88.8.
Percentiles are a useful statistical measure for analyzing data sets and understanding how they compare to others. To find the value at a particular percentile, you need to use the formula X = μ + Zσ, where X is the value at the desired percentile, μ is the mean of the data set, σ is the standard deviation of the data set, and Z is the z-score associated with the desired percentile. By using this formula, you can calculate percentiles for any data set and gain valuable insights into its distribution.
Calculating Percentiles
Percentiles are a statistical tool that is commonly used in data analysis. They are a way to measure the position of a partcular value within a data set. In simple terms, a percentile is a value below which a certain percentage of observations in a group fall.
To calculate the percentile of a data set, the following formula is used:
N = (P/100) x N
Where:
– n is the ordinal rank of the given value
– P is the percentile you want to calculate
– N is the total number of values in the dataset
In this formula, the value of P is expressed as a percentage, and it represents the percentage of data values that fall below the percentile you want to calculate. For example, if you want to calculate the 75th percentile of a dataset, P would be 75.
To use this formula, you need to first sort the data set in ascending order, from smallest to largest. Then, you can use the formula to determine the ordinal rank of the value you’re interested in.
For example, let’s say you have a data set with the following values:
2, 3, 5, 7, 8, 10, 12, 15, 18, 20
If you want to calculate the 90th percentile of this data set, you would first determine the value of n using the formula:
N = (90/100) x 10
N = 9
This tells us that the 90th percentile falls at the ninth value in the data set, which is 18.
The formula for calculating percentiles is n = (P/100) x N, where n is the ordinal rank of the given value, P is the percentile you want to calculate expressed as a percentage, and N is the total number of values in the dataset.
Source: statology.org
Calculating the 90th Percentile Using Mean and Standard Deviation
The 90th percentile is a statistical measure that represents the value below which 90% of the data falls. To calculate the 90th percentile, you need to know the mean and standard deviation of the data set. The formula to calculate the 90th percentile is X=μ + Zσ, were X is the value of the 90th percentile, μ is the mean, σ is the standard deviation, and Z is the z-score corresponding to the 90th percentile.
To find the z-score for the 90th percentile, you can use a standard normal distribution table, which lists the area under the curve to the left of a given z-score. Since the total area under the curve is equal to 1, the area to the left of the 90th percentile is 0.9. Using the table, you can find the z-score corresponding to an area of 0.9, which is 1.28.
Once you have the z-score of 1.28, you can plug it into the formula X=μ + Zσ to find the value of the 90th percentile. For example, if the mean is 50 and the standard deviation is 10, the value of the 90th percentile would be X=50 + 1.28(10) = 63.8.
In summary, to find the 90th percentile with mean and standard deviation, you need to follow these steps:
1. Find the z-score corresponding to the 90th percentile using a standard normal distribution table.
2. Plug the z-score into the formula X=μ + Zσ to find the value of the 90th percentile.
Finding Z-Score Using Mean, Standard Deviation, and Percentile
In statistics, a z-score is a measure of how many standard deviations a data point is from the mean. It is a useful tool for comparing different data sets and determining the significance of a particulr observation.
To find the z-score with mean and standard deviation and percentile, we need to use the following formula:
Z = (x – mean) / standard deviation
Where Z is the z-score, x is the value we want to convert to a z-score, mean is the mean of the data set, and standard deviation is the standard deviation of the data set.
To find the percentile corresponding to a given z-score, we can use a standard normal distribution table or calculator. This table or calculator provides the area under the normal distribution curve to the left of a particular z-score, which can be converted to a percentile.
Here are the steps to find the z-score with mean and standard deviation and percentile:
1. Determine the value of x that you want to convert to a z-score.
2. Find the mean and standard deviation of the data set.
3. Use the formula Z = (x – mean) / standard deviation to calculate the z-score.
4. Use a standard normal distribution table or calculator to find the area under the normal distribution curve to the left of the z-score.
5. Convert the area to a percentile by multiplying by 100%.
It is important to note that the z-score assumes that the data set follows a normal distribution. If the data set is not normally distributed, the z-score may not be an accurate measure of significance.
Conclusion
Percentiles are a powerful tool for understanding and analyzing data sets. By calculating the ordinal rank of a value within a data set, we can determine how that value compares to other values in terms of its relative position. This information can be particularly useful in fields such as education, health, and finance, where understanding how an individual’s performance or biometric measurements compare to others is essential. Additionally, the ability to calculate z-scores from given percentiles allows us to make inferences about the underlying distribution of a data set and can inform statistical analyses. percentiles are a valuable tool for anyone working with data and can provide valuable insights into patterns and trends that may not be imediately apparent from simply looking at individual values.
