Have you ever wondered if variance can be negative? Variance is a measure of how much a set of numbers vary from the average. It’s used to determine how spread out the values are in a data set or sample. And it’s an important tool for analyzing data and making predictions. But can variance be negative?
The short answer is no. Variance can never be negative. Here’s why: Variance is calculated by taking the difference betwen each value and the average, squaring it, then summing up all of those squared differences. The result is always positive because the squares make all of the differences positive — even if there are some negative values mixed in with the positives.
Let’s take an example to illustrate this point more clearly. Let’s say we have a data set with three values: 5, 4, and 3. We find the average by adding up all three numbers and dividing by three, which gives us 4 as the average. To find our variance, we take each number (5, 4, and 3) and subtract it from our average (4). That gives us 1 for 5-4; 0 for 4-4; and -1 for 3-4. We then square each number to get 1 for (1)2; 0 for (0)2; and 1 for (-1)2 — since squares are always positive — giving us a total variance of 2 (1+0+1=2). So although one of our numbers was negative (-1), our final variance was still positive (2).
So there you have it: variance can never be negative! Variance is calculated using squared differences that always come out positive, no matter how many negatives might be included in your initial data set or sample. This makes it an invaluable tool when analyzing data sets and making predictions — so now that you know that variance can never be negative, you can use this knowledge to your advantage!
Negative Variance: What Does It Mean?
When a variance is negative, it means that the actual results were worse than the expected or planned results. For example, if a company budgeted to make $10,000 in sales but only made $9,500, then the variance would be -$500. This means that the actual sales were $500 lower than what was expected or budgeted for. Similarly, if a company budgeted to spend $5,000 on expenses but spent $5,500 instead, then the variance would be -$500. This means that the actual expenses were $500 higher than what was planned for. A negative variance can be used to identify areas of cost overruns or underspending and can help inform decisions aout how resources should be allocated in order to maximize efficiency and profitability.
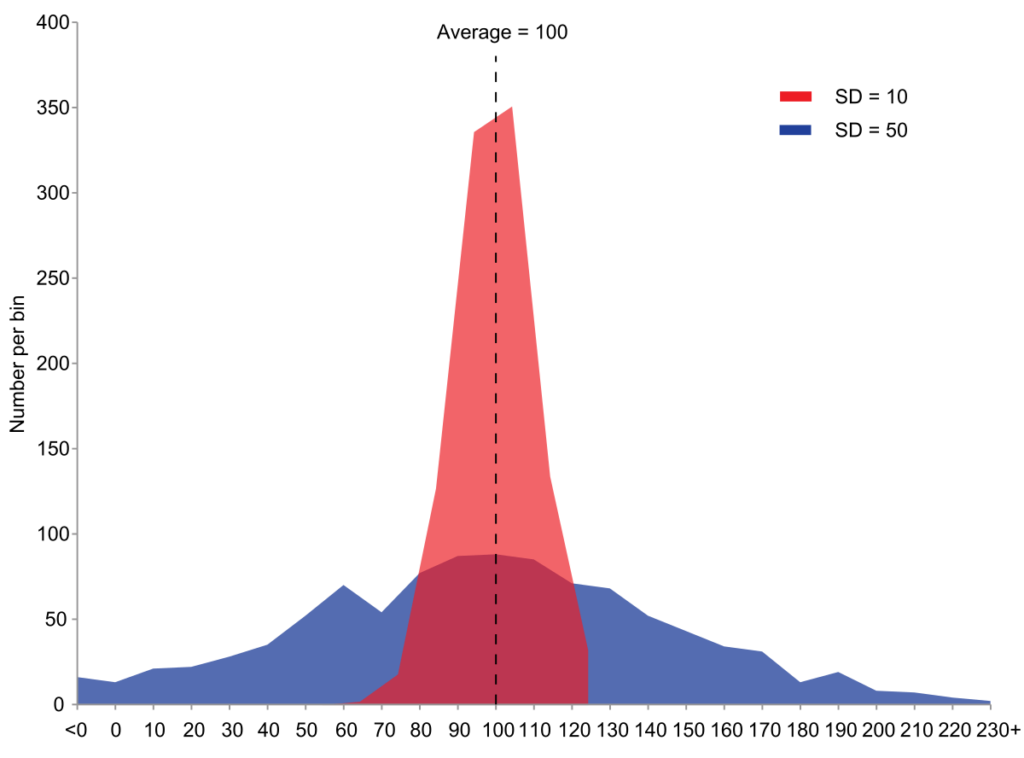
Negative Variances: Is It Possible?
No, variance cannot be negative. Variance is a measure of how much a set of numbers are spread out from the average value. A variance of zero would mean that all values in the set are equal to the average, and so any negative value would be impossible. If you take the difference between each number and the average and then square them, you will always get a non-negative result. Therefore, variance can never be negative.
Is Variance Always Positive?
Yes, variance is always positive. This is because variance measures the expected value of a squared number, which is always greater than or equal to zero. Variance helps us to measure how much a variable differs from its mean or average. As such, it provies an indication of how spread out the data points are in relation to the mean. It is calculated by taking each data point and subtracting the mean from it, then squaring this difference and summing up all these squared differences. This ensures that all differences are positive, which means that the variance will always be positive.
Negative Variance: Why is it Not Possible?
A variance cannot be negative because it is the sum of squared deviations from the mean. Since the sum of all deviations from the mean is always equal to zero, any positive deviations must be offset by an equal number of negative deviations. Squaring these deviations removes the negative values, resulting in a value that can never be less than zero. This means that a variance can never be negative and is always positive or zero.
Conclusion
In conclusion, variance cannot be negative. This is because the sum of all deviations from the mean always equals zero, meaning the negative and positive deviations cancel each other out. To get positive values, the deviations are squared. This is why variance can only take on a value of zero or higher, never negative. Understanding this principle can help students better understand how to calculate variance and use it to analyze data.
