Tan theta is one of the six trigonometric functions that are commonly used in mathematics. It is defined as the ratio of the side opposite to an angle (theta) to the side adjacent to that angle in a rght triangle. This function is widely used in various fields of study, including physics, engineering, and even finance.
To calculate the value of tan theta, we need to know the length of the opposite and adjacent sides of the angle. This is typically done by using the Pythagorean theorem and the basic trigonometric ratios of sine, cosine, and tangent.
For example, if we have a right triangle with an angle theta of 30 degrees, and the lengths of the adjacent and opposite sides are 3 and 1 respectively, we can calculate the value of tan theta as follows:
Tan theta = opposite/adjacent
Tan 30 = 1/3
Tan 30 = 0.577
In this case, the value of tan theta is approximately 0.577.
It is important to note that the value of tan theta can be positive, negative, or undefined, depending on the quadrant in which the angle lies. In the first quadrant (0 to 90 degrees), the value of tan theta is positive. In the second quadrant (90 to 180 degrees), it is negative. In the third quadrant (180 to 270 degrees), it is positive again, and in the fourth quadrant (270 to 360 degrees), it is negative.
Another important point to consider is that the value of tan theta can be infinite when the angle is a multiple of 90 degrees. This occurs because the adjacent side of the triangle becomes zero, which makes the denominator of the ratio (adjacent side) also zero. As a result, the value of tan theta is undefined.
Tan theta is a fundamental trigonometric function that is used to calculate the ratio of the opposite and adjacent sides of an angle in a right triangle. It is widely used in various fields of study and is an essential tool for solving many mathematical problems. However, it is important to be aware of the limitations of tan theta, such as its undefined value at certain angles and its positive or negative value depending on the quadrant in which the angle lies.
What Is The Value Of Tan θ?
The value of tan θ, which is the trigonometric ratio of the tangent function with respect to an angle θ, depends on the value of the angle itself. In general, the tangent of an angle is defined as the ratio of the length of the opposite side to the length of the adjacent side of a right-angled triangle that contains the angle. Therefore, the value of tan θ can range from 0 to infinity, depending on the value of the angle. For example, when the angle is 0 degrees, the value of tan θ is 0, while when the angle is 90 degrees, the value of tan θ is undefined or infinite. The table above proides the values of the trigonometric ratios for angles of 0 degrees and 90 degrees.
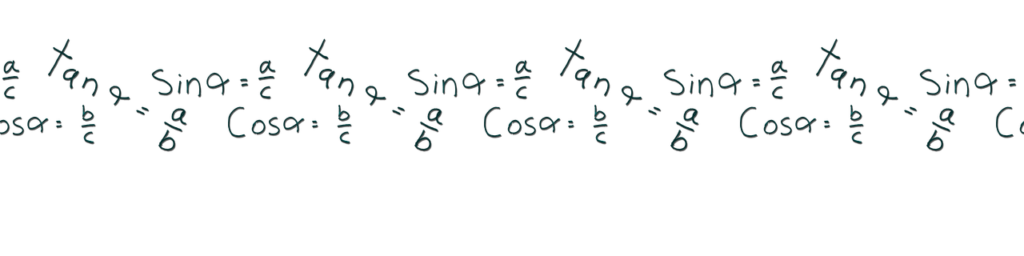
What Is The Formula Of Tan?
The formula for tan is based on the trigonometric ratios of sine and cosine. Specifically, the tangent of an angle is defined as the ratio of the sine of that angle to the cosine of that angle, as shown in the following formula:
Tan θ = sin θ / cos θ
In this formula, θ represents the angle in question, whch can be measured in degrees or radians. The value of tan θ indicates the ratio of the opposite side to the adjacent side of a right triangle that contains the angle θ.
It’s important to note that the tangent function is undefined for certain angles, such as when the cosine of the angle is equal to zero (i.e., when the angle is a multiple of 90 degrees). In these cases, the tangent is said to be “undefined” or “infinite.”
To summarize, the formula for the tangent of an angle is tan θ = sin θ / cos θ, which expresses the ratio of the sine to the cosine of the angle.
What Is Tan Theta Symbol?
The symbol “tan θ” represents the tangent function in mathematics. Tan θ is a trigonometric function that calculates the ratio of the length of the side opposite to an angle (θ) in a right-angled triangle to the length of the adjacent side. In other words, it is the ratio of the sine of the angle to the cosine of the angle. Tan θ is used in various fields of mathematics and science, including engineering, physics, and navigation. It is denoted by the abbreviation “tan” followed by the angle symbol (θ). The tangent function is one of the six trigonometric functions, the others bing sine, cosine, cosecant, secant, and cotangent.
What Gives Tan Theta?
Tangent theta is a trigonometric function that gives the ratio of the length of the side opposite to an acute angle theta in a right-angled triangle to the length of the side adjacent to that angle. In mathematical terms, the tangent of an angle theta is equal to the ratio of the opposite side to the adjacent side, i.e., tan(theta) = opposite/adjacent. However, it should be noted that this definition of tangent is only applicable to acute angles (angles between 0 and 90 degrees) and can only be used in right-angled triangles. The vale of tangent varies with the value of theta, and it is a periodic function with a period of π radians or 180 degrees.
Conclusion
The tangent function, denoted as tan θ, is one of the six basic trigonometric functions that relates the ratio of the length of the side opposite to an acute angle θ to the length of the adjacent side in a right triangle. It is defined as the ratio of sine to cosine, i.e., tan θ = sin θ/cos θ. The values of the tangent ratio for specific angles can be determined uing trigonometric tables or calculators. However, it is important to note that the tangent function is only defined for acute angles, and it can be used in various fields, such as physics, engineering, and mathematics, to solve problems involving triangles and angles.
