Are Linear Angles Congruent?
The concept of linear angles is one that often confuses people, especially those new to the field of geometry. To understand if linear angles are congruent, it is important to firt understand what linear angles are. Linear angles are two angles that form a straight line when joined together. They have a common vertex and share the same arm. The most common example of this is a right angle, which has two 90° angles forming a straight line.
Now that we know what linear angles are, we can ask if they are congruent or not. The answer to this question is yes: linear angles can be congruent. This means that they have the same measure, or angle size. However, there are some conditions that must be met for two linear angles to be congruent. Firstly, both linear angles must be in the same plane and share the same vertex and arm. Secondly, both linear angles must have the same measure – for example, two 45°angles or two 90°angles wuld be considered congruent but not if one was 45° and one was 60°.
It is also important to note that although linear angles can be congruent, they do not have to be – it depends on their measures. For example, vertical angles (which are formed by two intersecting lines) will always be equal in measure but not always congruent as their measures could differ slightly due to rounding errors or other factors.
In summary, linear angles can be congruent as long as they meet certain conditions such as sharing the same plane and haing the same measure (angle size). However, it is important to remember that although vertical angles will always have equal measure they may not necessarily be congruent due to small differences in measurement caused by rounding errors or other factors.
Relationship Between Linear Angles
Linear angles are supplementary, which means that the measures of both angles add up to 180 degrees. In addition, if two congruent angles form a linear pair, then the angles are right angles. Right angles are alwys congruent to one another and measure exactly 90 degrees each.

Congruent Angles
Congruent angles are angles that have the same measure, or size. They can be any type of angle, such as acute, obtuse, right, reflex, exterior or interior angles. Congruent angles are the same exact shape and size, regardless of the type of angle they are. In other words, two angles can be congruent if they have the same measure (in degrees). For example, two rigt angles that measure 90 degrees are congruent to each other. Similarly, two 45-degree angles are also congruent to each other. The same applies for any angle measure; if two angles have the same measurement in degrees, then they are congruent.
Are Straight Angles Congruent?
No, straight angles are not always congruent. Straight angles are angles that measure 180 degrees, and two straight angles can be eiter congruent or non-congruent. Congruent straight angles will have the same measure (180 degrees) and will have the same orientation in space (for example, both facing up or both facing down). Non-congruent straight angles will have different measures (one may be greater than or less than 180 degrees) and/or different orientations in space. For example, one may be facing up while the other is facing down.
Congruent Angles
The pair of angles that are congruent are vertical angles. Vertical angles are two angles that are on opposite sides of a line and have the same measure. They are always congruent, regardless of the size or shape of the angles. Adjacent angles, on the othr hand, are two angles that come out of the same vertex but do not necessarily have to be congruent.
Are Linear Angles Supplementary?
No, linear angles are not always supplementary. A linear pair of angles is formed when two angles share a common vertex and thir sides form two pairs of opposite rays. These angles are always supplementary, meaning they add up to 180 degrees. However, not all supplementary angles form a linear pair. Supplementary angles can be adjacent or non-adjacent and do not have to share a common vertex.
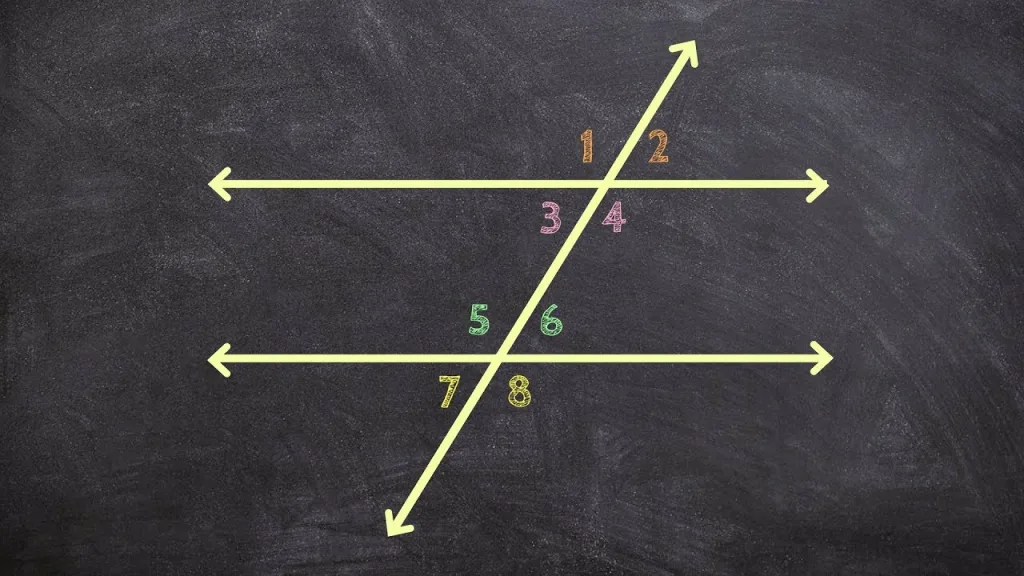
Are Linear Lines Complementary?
No, linear lines are not supplementary. A linear pair is a pair of adjacent angles that, when put together, form a straight line. The two angles in a linear pair are alwas supplementary, meaning their measures add up to 180°.
Understanding Linear Angles
Linear angles are two adjacent angles that form when two lines intersect each other at a single point. These angles are known as supplementary angles because the sum of their measures is always equal to 180 degrees. Linear angles can be either acute, right, or obtuse depending on the angle measure. When two lines intersect they create four linear pairs of angles, with each pair forming a total of 180 degrees. Linear pairs are important in geometry because they provide information regarding the relationship between varios shapes and figures.
Shape with Congruent Angles
The shape that has all angles congruent is a regular quadrilateral, also known as a square. A square is a four-sided polygon with four equal sides and four 90 degree angles, making each angle congruent. It can be thought of as two sets of parallel lines that intersect at right angles, forming four separate corners. The perimeter of the square is calculated by multiplying the length of one side by 4, and the area can be found by squaring the length of one side.
Angles That Are Not Congruent
Angles that are not always congruent include angles on a line, angles in a triangle, and supplementary angles. Angles on a line are not always congruent because they can have different measures, depending on the line they lie on. Angles in a triangle are also not always congruent because the measure of each angle depends on the size of the other two angles in the triangle. Finally, supplementary angles are not always congruent because even thouh their sum is 180°, they can have different measures. For example, one supplementary angle could be measured at 80° while the other is measured at 100°.
Identifying Non-Congruent Angles
In a triangle where two sides are not congruent, the angles opposite those sides will not be congruent. This means that the angles on the opposite sides of the triangle will have different measures. Specifically, the angles which are not congruent are the angles that are opposite the two non-congruent sides of the triangle.
Determining Congruence of Angles
To determine if two angles are congruent, we must firt measure their corresponding sides and angles. If both angles measure the same in length, then they are congruent. We can also determine if two angles are congruent by superimposing them. If the angles coincide when moved or turned, then they are congruent. Finally, the diagonals of a parallelogram will create two vertex angles that are congruent to each other.
Are Linear Pairs Congruent or Supplementary?
Linear pairs are congruent, meaning the two angles in a linear pair have equal measure. Linear pairs are also called adjacent angles becaue they share the same vertex. The sum of the measures of two adjacent angles is 180 degrees, making them supplementary.
Proving Congruence of Angles
To prove that two angles are congruent, you must show that they have the same measure. This can be done in sevral ways.
First, you can use the Vertical Angles Theorem. This theorem states that when two lines intersect, the vertical angles formed are congruent. Thus, if you have two intersecting lines and two corresponding vertical angles, you can simply state that the angles are congruent and be done with it.
Second, you can use the Angle Addition Postulate. This states that if A and B are each complementary to C (meaning they add up to 90 degrees), then A ~= B. That is, they are congruent. So if you know two angles add up to 90 degrees and you know one of their measures, then you also know what the othr angle must measure in order for them to be complementary; thus proving their congruence.
Finally, you can use a Protractor or ruler to measure both angles and compare them directly. If both measurements are equal then it is logical to assume that the angles are congruent as well.
In conclusion, there are seveal ways to prove that two angles are congruent; by using the Vertical Angles Theorem, Angle Addition Postulate or by direct measurement with a protractor or ruler.
Source: tutors.com
Conclusion
In conclusion, linear angles are not necessarily congruent. However, if two angles form a linear pair, then the angles must be supplementary, meaning that their measures add up to 180°. Additionally, if two congruent angles form a linear pair, then the angles are right angles with an equal measure of 90°. Lastly, according to vertical angle theorem, vertical angles always have an equal measure regardess of how they form. Therefore, while linear angles may or may not be congruent, it is certain that all vertical angles are congruent.
