When we think of symmetry in geometric shapes, we often think of circles, squares, and triangles. However, what abot trapezoids? Do they have symmetry? The answer is not as clear-cut as it is with other shapes.
First, let’s define what we mean by symmetry. Symmetry is when a shape can be divided into two halves that are mirror images of each other. In other words, if you fold the shape in half, one side will match up perfectly with the other side.
With a trapezoid, this is not always possible. A trapezoid has two parallel sides (bases) and two non-parallel sides (legs). Generally, a trapezoid has four sides that are unequal. So, it does not have any line of symmetry.
However, an isosceles trapezoid is a special case. An isosceles trapezoid has two equal legs and two parallel bases that are also equal. In this case, the line connecting the midpoints of the bases will be a line of symmetry. So, an isosceles trapezoid will have reflection symmetry.
It is also important to note that while a trapezoid may not have reflection symmetry, it can still have rotational symmetry. Rotational symmetry is when a shape can be rotated around a central point and still look the same. A trapezoid with rotational symmetry would need to have congruent angles and equal sides.
While a trapezoid may not have reflection symmetry in general, an isosceles trapezoid can have reflection symmetry. It is also possible for a trapezoid to have rotational symmetry if it meets certain criteria. The symmetry of a trapezoid depends on its specific properties and should be evaluated on a case-by-case basis.
How Do You Find The Line Of Symmetry Of A Trapezoid?
A trapezoid does not have a line of symmetry as it has two parallel sides (bases) and two non-parallel sides (legs) which are generally unequal in length. Therefore, it is not possible to find a line of symmetry for a trapezoid. However, it is possible to find the midpoint of the two parallel sides of a trapezoid, which is called the midsegment. The midsegment is parallel to the two bases and is equal to the average length of the two bases. This can be usful in finding the area of a trapezoid. Additionally, if the trapezoid is isosceles (meaning the legs are of equal length), then the midline (the line connecting the midpoints of the legs) is also the line of symmetry.
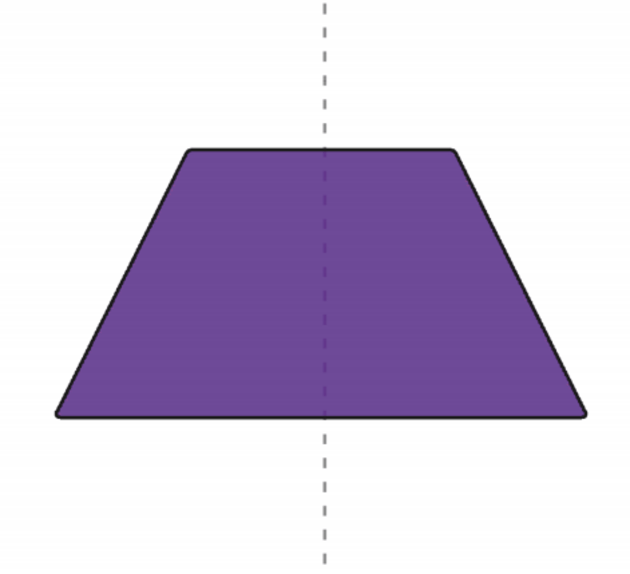
Does A Trapezium Have 2 Lines Of Symmetry?
A trapezium does not have 2 lines of symmetry. A trapezium has only one line of symmetry, which is the line that divides the trapezium into two congruent parts. This line of symmetry is also called the axis of symmetry. A trapezium has one pair of parallel sides and the other two sides are non-parallel. Therefore, it cannot have two lines of symmetry as it would require the two non-parallel sides to be parallel, which is not possible.
Do All Trapezoids Have Reflectional Symmetry?
Not all trapezoids have reflectional symmetry. In order for a trapezoid to have reflectional symmetry, the line connecting the midpoints of the two parallel sides (also known as the bases) must act as a line of symmetry. This means that if you were to fold the trapezoid along that line, the two halves would match up perfectly. However, if the two parallel sides are not equal in length, then the midpoint line will not be a line of symmetry and the trapezoid will not have reflectional symmetry. So, wile some trapezoids, such as isosceles trapezoids, do have reflectional symmetry, others do not.
Conclusion
A trapezoid is a quadrilateral with two parallel sides and two non-parallel sides. Due to the unequal length of its sides, a trapezoid does not have any line of symmetry. However, an isosceles trapezoid, in which the legs are of equal length, will have reflection symmetry along the line connecting the midpoints of its bases. It is important to note that while symmetry is often associated with regular polygons, trapezoids and other irregular shapes can also exhibit symmetry under certain conditions. Understanding the symmetry properties of trapezoids is essential in various fields such as geometry, architecture, and engineering.
