Logarithms are mathematical functions that are commonly used in various fields, including mathematics, science, and finance. They are used to solve equations involving exponential growth or decay, as well as to simplify complex calculations. However, there are instances when we want to eliminate logarithms from an equation in order to solve it more easily. This process of getting rid of logarithms is known as “canceling log.”
To cancel logarithms, we need to apply the inverse function of logarithms, which is exponentiation. Exponentiation is the process of raising a base to a certain power. The key idea behind canceling logarithms is that exponentiation undoes the effect of logarithms.
Let’s consider a simple example to illustrate how we can cancel logarithms. Suppose we have the equation:
Ln(x) = 2
In this equation, ln(x) represents the natural logarithm of x. To cancel the logarithm, we need to raise both sides of the equation to the exponent of the base of the logarithm, which is e (approximately 2.71828). By doing so, we can eliminate the logarithm and solve for x.
Raising both sides of the equation to the power of e, we get:
E^(ln(x)) = e^2
Now, according to the properties of logarithms and exponentiation, the base and the logarithm cancel each other out. Therefore, the left-hand side simplifies to just x:
X = e^2
By evaluating e^2 (which is approximately 7.38906), we find that x is approximately 7.38906.
This simple example demonstrates how we can cancel logarithms by raising both sides of an equation to the exponent of the base of the logarithm. By doing so, we eliminate the logarithm and solve for the variable.
It’s important to note that canceling logarithms can be applied to logarithms with any base, not just the natural logarithm. The same principle applies – raise both sides of the equation to the exponent of the base to eliminate the logarithm.
Canceling log involves applying the inverse function of logarithms, which is exponentiation. By raising both sides of an equation to the exponent of the base of the logarithm, we can eliminate the logarithm and solve for the variable. This technique is useful for simplifying equations and solving problems in various fields of study.
What Is The Opposite Of Log?
The opposite, or inverse, of a logarithm function is an exponential function. In other words, if we have a logarithm function that takes a number and returns the power to which a base must be raised to obtain that number, the inverse function will take a number and return the base raised to that power.
To be more specific, let’s consider the base 10 logarithm function, also known as the common logarithm. This function is denoted as log(base 10) or simply log. For example, log(100) = 2 because 10 raised to the power of 2 equals 100.
The inverse function of log(base 10) is the exponential function with base 10, denoted as 10^x. For example, 10^2 equals 100, so if we apply the inverse function to the value 2, we get 10^2 = 100.
In general, the inverse of any logarithm function log(base b) is the exponential function with base b. The inverse function undoes the work of the logarithm, allowing us to find the original number that was used as the input to the logarithm function.
The opposite or inverse of the log function is an exponential function with the same base. It allows us to find the original number given the result of a logarithm calculation.
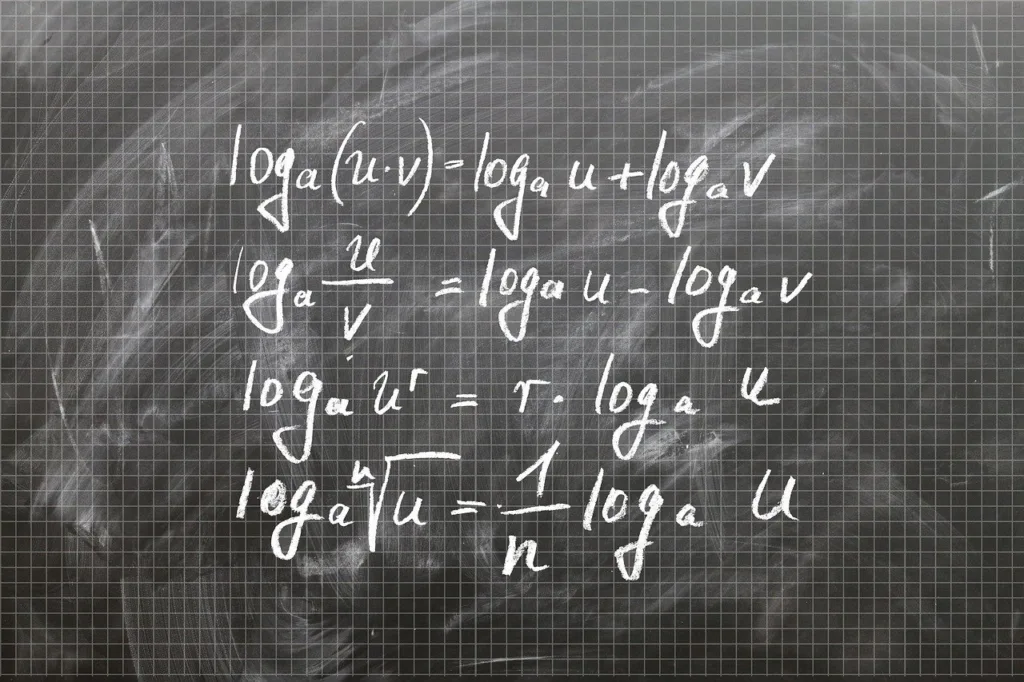
How Do You Get Rid Of Log In An Equation?
To eliminate logarithms from an equation, follow these steps:
1. Identify the logarithmic terms in the equation. Logarithmic terms typically appear as expressions with a logarithm function, such as log(base) or ln (natural logarithm).
2. Determine the base of the logarithm. The base is the subscript value written after the “log” or “ln” function. For example, in log(base 10), the base is 10, and in ln, the base is the mathematical constant “e” (approximately 2.718).
3. Raise both sides of the equation to the exponent of the base. This means that you will raise both sides to the power of the base of the logarithm. By doing this, the equation transforms from a logarithmic form to an exponential form.
4. Simplify the equation by performing the necessary calculations on both sides. Remember to apply the exponent rules, such as multiplying exponents when raising a power to another power.
5. Solve the resulting exponential equation for the variable. This may involve further algebraic manipulations, such as factoring, combining like terms, or isolating the variable on one side of the equation.
6. Check the obtained solution by substituting it back into the original equation. Ensure that the solution satisfies the equation and does not introduce any extraneous solutions.
Here is an example illustrating these steps:
Original equation: log(base 2)(x) = 3
Step 1: Identify the logarithmic term: log(base 2)(x)
Step 2: The base of the logarithm is 2.
Step 3: Raise both sides to the exponent of the base:
2^(log(base 2)(x)) = 2^3
Step 4: Simplify the equation:
X = 8
Step 5: Solve for the variable:
The solution is x = 8.
Step 6: Check the solution:
Log(base 2)(8) = 3
Since log(base 2)(8) does indeed equal 3, the solution is valid.
By following these steps, you can effectively eliminate logarithms from an equation and solve for the variable.
What Cancels A Natural Log?
A natural log can be cancelled by raising the base of the natural log (e, approximately 2.718) to the power of the quantity inside the log. This is based on the properties of logarithms, specifically the property that states that the coefficient in front of the natural log can be rewritten as the exponent raised by the quantity inside the log. By raising the base to the power of the quantity inside the log, both the base and the natural log can be eliminated, resulting in the original quantity.
To summarize, what cancels a natural log is raising the base of the natural log to the power of the quantity inside the log. This eliminates both the base and the natural log, leaving the original quantity.
Conclusion
When we encounter logarithms in an equation, we can eliminate them by raising both sides of the equation to the same exponent as the base of the logarithm. By doing so, we effectively cancel out the logarithm and are left with an exponential expression. Specifically, when dealing with natural logarithms, which have a base of , raising both sides to the power of will remove both the and the natural log. This process allows us to simplify equations and solve for the unknown variables more easily. Therefore, understanding how to cancel logarithms is a valuable skill in mathematics and can help us in various applications, such as in solving exponential growth or decay problems.
