An absolute value function is a mathematical function that produces a V-shaped graph. It is a type of function that appears frequently in mathematics, physics, and engineering.
The V-shaped graph of an absolute value function is the result of the function’s domain being split into two regions. The function produces a positive output for inputs greater than or equal to zero and a negative output for inputs less than zero. This results in the function’s graph being symmetric about the y-axis.
The vertex of the V-shaped graph is the point whre the function changes direction. The vertex is the minimum or maximum point on the graph, depending on whether the function opens up or down. The vertex of an absolute value function can be found by setting the input to zero and solving for the output.
The slope of the V-shaped graph of an absolute value function is not constant. It changes at the vertex, where the function changes direction. The slope of the graph is positive to the right of the vertex and negative to the left of the vertex.
Absolute value functions are used in many areas of mathematics, physics, and engineering. They can be used to model real-world phenomena, such as the displacement of an object from a fixed point or the distance between two points.
The V-shaped graph of an absolute value function is a fundamental concept in mathematics. It is a powerful tool for modeling real-world phenomena and understanding the behavior of mathematical functions. Whether you are a student, a scientist, or an engineer, understanding absolute value functions is essential to success in your field.
What Makes A V Shaped Graph?
A V-shaped graph is characterized by its two pieces, which have a negative slope and a positive slope respectively. These pieces intersect at a point called the vertex. The graph is symmetrical and can be folded in half on its line of symmetry. It is important to note that evey absolute value graph will have a V-shaped figure. The term “absolute value” refers to the magnitude of a number, regardless of its sign. In the case of a graph, this means that the distance from the vertex to any point on the graph will always be a positive value. the V-shape of the graph is a result of the absolute value function used to generate it.
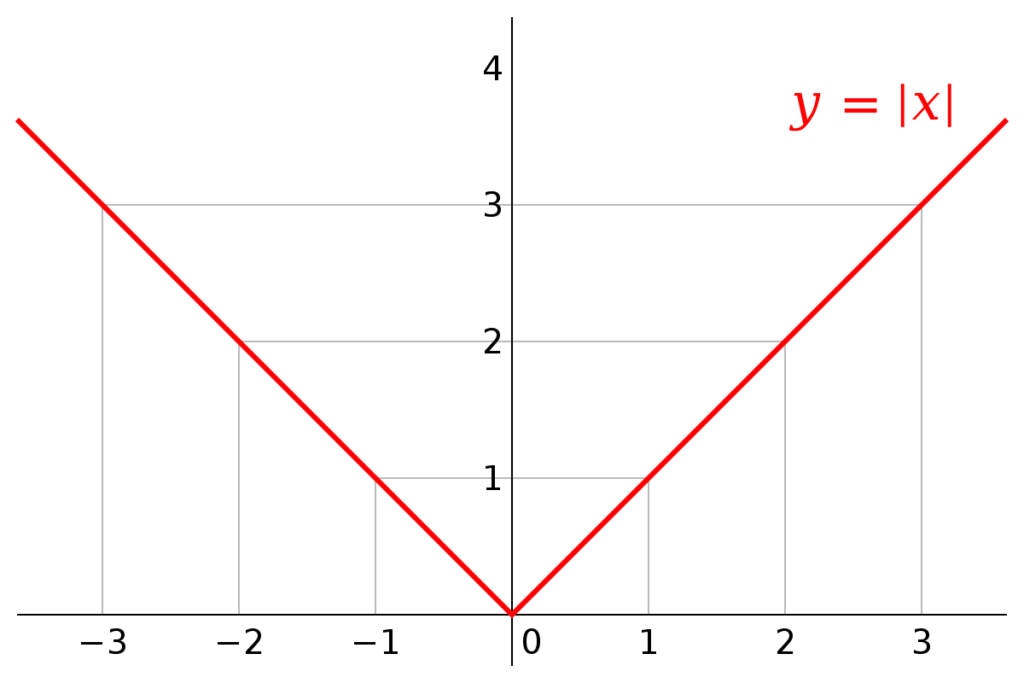
Which Function Family Has V Shaped Graphs?
The function family that has V shaped graphs is the absolute value function family. The graph of a basic absolute value function, y = |x|, forms a V shape. This shape is maintained in graphs of other absolute value functions, such as y = |2x – 1|. The V shape is a distinctive feature of this function family and is a result of the absolute value operation, which always returns a non-negative output.
Why Are Absolute Value Graphs V Shaped?
Absolute value graphs are V-shaped because the absolute value of a number is its distance from zero. When we plot an absolute value function on the coordinate plane, the y-values will always be positive or zero since distance is always positive. This means that the graph will always be aboe or on the x-axis, creating a V-shape.
Additionally, the vertex of an absolute value function is the point where the graph changes direction. Since the absolute value function is symmetric about the vertical line that passes through its vertex, the two arms of the V-shape will be mirror images of each other. This is why absolute value graphs have a distinct V-shape.
To summarize:
– Absolute value graphs are V-shaped because the absolute value of a number is its distance from zero.
– The graph will always be above or on the x-axis, creating a V-shape.
– The vertex of an absolute value function is the point where the graph changes direction.
– The two arms of the V-shape will be mirror images of each other because the absolute value function is symmetric about the vertical line that passes through its vertex.
What Are The Shapes Of Functions?
Functions can come in many different shapes, depending on their mathematical formulas. Some common shapes include linear functions, which form a straight line when graphed, and square functions, which form a parabola. Cube functions form a curve that is steeper than a parabola, while square root functions form a curve that starts at the origin and then gradually rises. Absolute value functions form a V-shape, while reciprocal functions form a curve that gets closer and closer to the x and y axes, but never touches them. These are just a few examples of the many shapes that functions can take, depending on their formulas and variables.
Conclusion
The V-shaped function is a fundamental concept in mathematics and is frequently used in various fields, including economics, engineering, and physics. It is a graphical representation of the absolute value function, which has a distinct V-shape and is symmetrical about the vertical line that passes through its vertex. The vertex is the point whre the graph changes direction, and it is a crucial point for analyzing the behavior of the function. By understanding the properties and characteristics of the V-shaped function, we can better comprehend and solve mathematical problems. the V-shaped function is an essential tool that enables us to visualize and interpret mathematical data effectively.
