When it coes to graphing a parabola, it is important to understand the concept of roots. The roots of a parabola are the points where the parabola intersects with the x-axis. To find the roots of a parabola, you need to set the equation equal to zero and solve for x.
The equation of a parabola in standard form is y = ax^2 + bx + c. To find the roots of the parabola, you need to set y equal to zero and solve for x. This gives you the quadratic equation ax^2 + bx + c = 0. You can solve for x using the quadratic formula, completing the square, or factoring the equation.
The quadratic formula is x = (-b ± sqrt(b^2 – 4ac)) / 2a. This formula gives you the two possible values of x where the parabola intersects with the x-axis. If the value under the square root is negative, then the parabola does not intersect with the x-axis, meaning it has no roots.
Completing the square is another method for finding the roots of a parabola. This involves rearranging the equation into the form y = a(x – h)^2 + k, where (h, k) is the vertex of the parabola. Setting y equal to zero and solving for x gives you the roots of the parabola.
Factoring is another method for finding the roots of a parabola. If the equation can be factored into two binomials, then the roots are the x-values that make each binomial equal to zero.
The number of roots a parabola has depends on the value of the discriminant, b^2 – 4ac. If the discriminant is positive, then the parabola has two real roots. If the discriminant is zero, then the parabola has one real root. If the discriminant is negative, then the parabola has no real roots, but it does have two complex roots.
Understanding the roots of a parabola is essential for graphing it accurately. By knowing where the parabola intersects with the x-axis, you can plot the points and create an accurate graph. Whether you use the quadratic formula, completing the square, or factoring, solving for the roots of a parabola is a crucial step in the graphing process.
What Is The Root Form Of A Parabola?
The root form of a parabola is a way to express a quadratic equation in the form y=a(x−r)(x−s), where a is the coefficient of the quadratic term, and r and s are the roots or x-intercepts of the parabola. The roots of the parabola are the points where the parabola intersects the x-axis. By knowing the roots and the coefficient a, we can easily graph the parabola. The roots of the parabola can be found by solving the quadratic equation, whih is obtained by setting y=0 in the equation y=a(x−r)(x−s). The Factor-Root Theorem states that if a quadratic equation of the form y=ax²+bx+c can be factored as y=a(x-r)(x-s), then its roots are r and s. The root form of a parabola is a useful tool in graphing and analyzing quadratic functions.
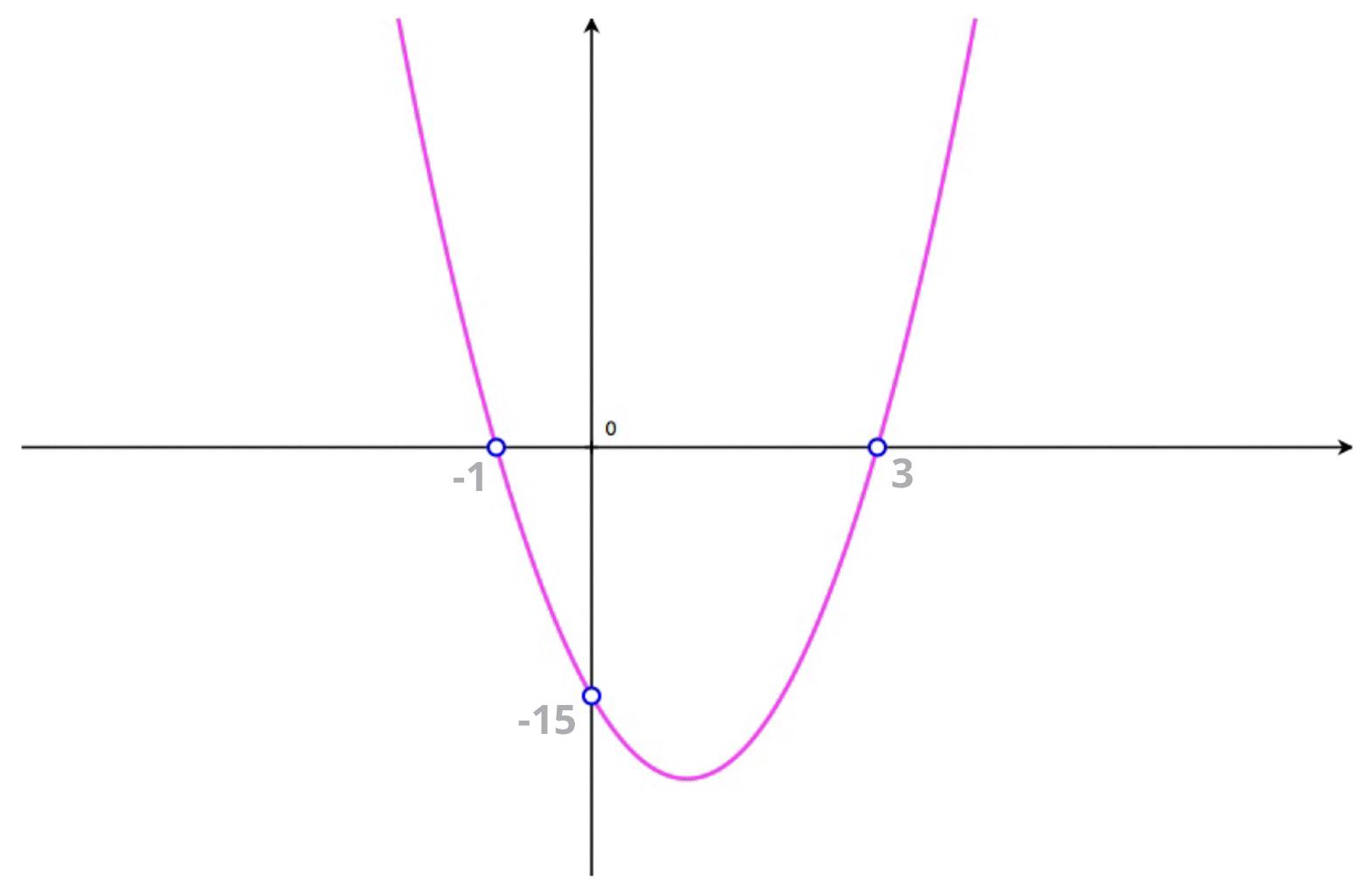
How Do You Find The Roots Zeros Of A Parabola?
To find the roots or zeros of a parabola, we need to look for the points on the parabola where it intersects the horizontal x-axis, which is the line y=0. In mathematical terms, we can find thse points by solving the quadratic equation ax²+bx+c=0 where a, b, and c are coefficients of the quadratic function.
There are different methods to solve quadratic equations, such as factoring, completing the square, or using the quadratic formula. Once we have found the solutions for x in the equation, these values represent the x-coordinates of the points where the parabola intersects the x-axis.
It’s important to note that a parabola can have two, one, or no real roots depending on the discriminant b²-4ac of the quadratic equation. If the discriminant is positive, the parabola intersects the x-axis at two distinct points, which are the real roots. If the discriminant is zero, the parabola touches the x-axis at one point, which is a real root with multiplicity 2. If the discriminant is negative, the parabola does not intersect the x-axis, and there are no real roots.
The roots or zeros of a parabola can be found by solving the quadratic equation ax²+bx+c=0 and looking for the x-coordinates of the points where the parabola intersects the x-axis. The number and nature of these roots depend on the discriminant of the equation.
Does A Parabola Have 2 Roots?
The answer to whether a parabola has 2 roots or not depends on the value of its parameter, which is denoted by b. When the value of b is between -2 and 2, the parabola has no roots, meaning it does not intersect with the x-axis at any point. On the oter hand, when b equals to 2 or -2, the parabola has only one root, which means it touches the x-axis at a single point.
However, when the value of b is greater than 2 or smaller than -2, the parabola has two roots, meaning it intersects the x-axis at two distinct points. It is important to note that the roots of a parabola are also known as its x-intercepts or zeros, and they are the points where the parabola crosses the x-axis.
The number of roots that a parabola has depends on the value of its parameter b. When b is between -2 and 2, the parabola has no roots, when b equals to 2 or -2, the parabola has one root, and when b is greater than 2 or smaller than -2, the parabola has two roots.
Conclusion
Understanding the roots of a parabola is crucial in graphing quadratic functions. The zeros or roots of a parabola are the points where the parabola intersects the x-axis or the line y=0. These points can be found by solving the quadratic equation ax2+bx+c=0, where a, b, and c are constants. The number of roots a parabola has depends on the value of the discriminant, whch is b2-4ac. If the discriminant is greater than zero, then the parabola has two distinct roots. If the discriminant is equal to zero, then the parabola has one repeated root. If the discriminant is less than zero, then the parabola has no real roots. Overall, having a solid understanding of the roots of a parabola can greatly assist in visualizing and accurately graphing quadratic functions.
