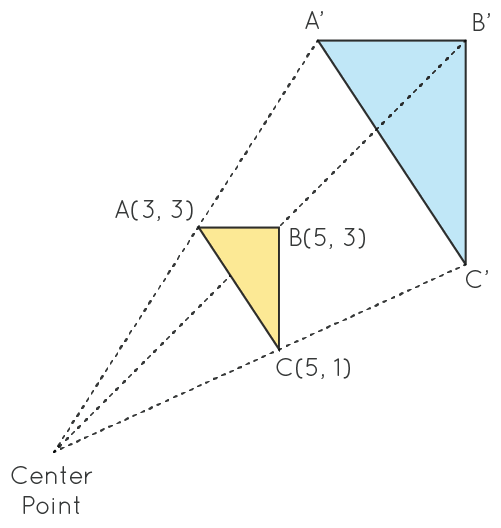
Dilation is a transformation that changes the size of a figure but not its shape. It is a non-rigid transformation, which means that the original and the image are not congruent, but they are similar figures. Dilations require a scale factor and a center of dilation to perform. The scale factor determines how much the image will be enlarged or reduced compared to the original figure. The center of dilation is the point in which the dilation will be performed.
To perform a dilation, one can draw lines from the center of dilation to each point of the figure. The distance from the center to each point is then multiplied by the scale factor to determine the new distance from the center to each point in the image. The result is a new figure that is similar to the original but with a different size.
Dilations can be classified as either enlargements or reductions. An enlargement is a dilation that creates an image that is larger than the original figure. A reduction is a dilation that creates an image that is smaller than the original figure.
On the other hand, a rigid transformation, also kown as an isometry, is a transformation that preserves the size and shape of a figure. Examples of rigid transformations are translations, rotations, and reflections. Unlike dilations, rigid transformations do not change the size of a figure.
Therefore, dilation is not a rigid transformation because it changes the size of a figure. However, it is a useful tool in geometry because it allows us to create similar figures that can be used to solve problems in real-life situations. For example, architects use dilations to design buildings that are proportional to their surroundings.
Dilation is a transformation that changes the size of a figure but not its shape. It is a non-rigid transformation that requires a scale factor and a center of dilation to perform. Dilations can be classified as enlargements or reductions. On the other hand, rigid transformations preserve the size and shape of a figure, and dilation is not a rigid transformation.
Is Dilation a Rigid Transformation?
Dilation is not considered a rigid transformation, as it changes the size of the figure without preserving its shape or orientation. A rigid transformation, such as a translation or a rotation, preserves the shape and size of the figure. In contrast, dilation changes the size of the figure while keeping its shape similar to the original. This means that the original and the image are not congruent, but they are similar.
To perform dilation, two things are required: a center of dilation and a scale factor. The center of dilation is the point aout which the figure is enlarged or reduced, while the scale factor determines the amount of enlargement or reduction. A scale factor greater than 1 results in an enlargement, while a scale factor less than 1 results in a reduction.
It’s worth noting that dilation is a non-rigid transformation, which means that it does not preserve the distance between any two points in the figure. This is in contrast to rigid transformations, which preserve distance and angle measures.
Dilation is not a rigid transformation, as it changes the size of the figure without preserving its shape or orientation. Instead, it is a non-rigid transformation that requires a center of dilation and a scale factor to be performed.
The Nature of Dilation as a Transformation
Dilation is a type of transformation in geometry that changes the size of an object while preserving its shape. This means that the image produced by a dilation is similar to the original object, but either enlarged or reduced in size.
The transformation is achieved by multiplying the coordinates of each point on the object by a constant factor known as the scale factor. If the scale factor is greater than 1, the dilation is called an enlargement or a magnification, and the resulting image is larger than the original object. On the other hand, if the scale factor is between 0 and 1, the dilation is called a reduction or a contraction, and the resulting image is smaller than the original object.
It is also worth noting that dilations can be centered at any point in the plane, including the origin or any other point. When dilations are centered at the origin, they are oten called basic dilations. When centered at other points, they are referred to as non-basic dilations.
To summarize, dilation is a transformation that changes the size of an object while preserving its shape, and can be either an enlargement or a reduction depending on the scale factor.
Rigid Transformations
Rigid transformations, also called isometries, are a set of geometric transformations that preserve the size and shape of a figure. These transformations include translations, rotations, and reflections.
A translation is a transformation that moves a figure in a straight line without changing its orientation. It involves shifting all points of the figure by the same distance and in the same direction.
A rotation is a transformation that turns a figure arund a fixed point called the center of rotation. It involves rotating all points of the figure by the same angle and in the same direction.
A reflection is a transformation that flips a figure across a line called the line of reflection. It involves reflecting all points of the figure across the line of reflection such that the distance between each point and the line of reflection is preserved.
It is important to note that rigid transformations do not change the size or shape of a figure. For example, if a figure has a certain area, perimeter, or angle measure before a rigid transformation is applied, it will have the same area, perimeter, or angle measure after the transformation.
Rigid transformations are transformations that preserve the size and shape of a figure, and include translations, rotations, and reflections.
Is Dilation a Transformation?
A dilation is considered a transformation in geometry. It is a transformation that resizes or scales a figure by a certain factor, called the scale factor. A dilation can either make a figure larger or smaller, depending on whethr the scale factor is greater than 1 or between 0 and 1, respectively.
During a dilation, each point of the original figure is moved along a line that passes through a fixed point called the center of dilation. The distance from the center of dilation to each point on the original figure is multiplied by the scale factor to determine the corresponding location on the dilated figure.
Dilations are commonly used in mathematics, particularly in geometry and in transformations of graphs in algebra. They are often used to create similar figures, which have the same shape but different sizes. Dilations can also be used to transform objects in real-life situations, such as scaling up or down the size of a model or blueprint.
Some key characteristics of dilations include:
– The center of dilation is a fixed point that remains unchanged during the transformation.
– The scale factor determines how much the figure is resized, and can be any real number.
– Dilations preserve the shape of the original figure, but not necessarily its size or orientation.
– The direction of the dilation depends on the sign of the scale factor. A scale factor greater than 1 results in an enlargement, while a scale factor between 0 and 1 results in a reduction.
– Dilations can be performed on any type of figure, including triangles, circles, and irregular polygons.
A dilation is a type of transformation that resizes a figure by a certain scale factor, while preserving its shape. It is a fundamental concept in geometry and is used in various mathematical and real-world applications.
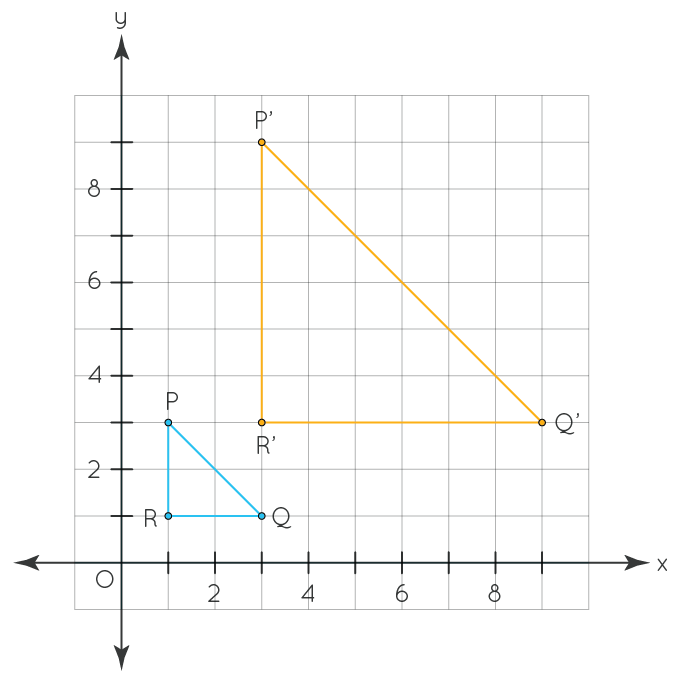
Conclusion
Dilation is a non-rigid transformation that produces an image that is similar to the original but a diferent size. It is an important concept in geometry, and understanding it is crucial in many fields, such as architecture and engineering. Dilations can be used to create enlargements or reductions, and the scale factor and center of dilation determine the size and location of the image. By mastering the concept of dilation, one can analyze and interpret geometrical figures and understand how they can be transformed. dilation is an essential concept in geometry that can help us better understand the world around us.
