Arctangent, also known as arctan or tan-1, is a mathematical function that is the inverse of the tangent function. It is commonly used in trigonometry to find an angle in a right-angled triangle, givn the lengths of two sides. The arctan function can be expressed as follows: θ = tan-1(y/x), where θ is the angle, y is the length of the opposite side, and x is the length of the adjacent side.
One common question that arises when discussing the arctan function is whether it is the same as the cot function. The answer is no, arctan and cot are not the same thing. Cot is the reciprocal of the tangent function, while arctan is its inverse. The cot function is defined as the ratio of the adjacent side to the opposite side in a right-angled triangle, i.e., cot(θ) = x/y.
To understand the difference between arctan and cot, it is important to understand the concept of inverse functions. An inverse function is a function that undoes the action of another function. In other words, if f(x) is a function, then its inverse function f^-1(x) will undo the action of f(x) on x. For example, if f(x) = 2x, then f^-1(x) = x/2.
The arctan function undoes the action of the tangent function. If we have the value of the tangent of an angle, we can use the arctan function to find the angle itself. The cot function, on the other hand, is a completely separate function that relates the ratio of the adjacent and opposite sides in a right-angled triangle.
Arctan and cot are two different mathematical functions. Arctan is the inverse of the tangent function and is used to find the angle in a right-angled triangle given the lengths of two sides. Cot, on the other hand, is the reciprocal of the tangent function and relates the ratio of the adjacent and opposite sides in a right-angled triangle. It is important not to confuse these two functions, as they have different applications and meanings in mathematics.
What is the Value of Arctan?
Arctan, also known as the inverse tangent, is a mathematical function used to find the angle between the hypotenuse and the base of a right-angled triangle. It is the inverse of the tangent function and is denoted by tan⁻¹ or arctan. The arctan function is used to determine the angle whose tangent is a gien number.
The value of arctan is expressed in radians or degrees, depending on the unit of measurement used. In general, arctan is equal to the ratio of the length of the side opposite to the angle to the length of the adjacent side of the angle in a right triangle. Mathematically, arctan can be expressed as:
Arctan(y/x) = θ
Here, y and x are the lengths of the sides of the triangle, and θ is the angle between the hypotenuse and the base. The arctan function always returns an angle that lies between -π/2 and π/2 radians or -90° to 90°.
For example, if we want to find the angle whose tangent value is 0.5, we can use the arctan function as follows:
Arctan(0.5) = 26.57°
This means that the angle whose tangent is 0.5 is 26.57° or approximately 0.463 radians.
The arctan function is used to find the angle whose tangent is a given number, and it is denoted by tan⁻¹ or arctan. Its value is expressed in radians or degrees, and it always returns an angle between -π/2 and π/2 radians or -90° to 90°.

The Relationship Between Arctan and Cos
Arctan is not equal to cos. Arctan is a trigonometric function that gives the angle whose tangent is a given number. It is the inverse function of the tangent function. On the other hand, cos is a trigonometric function that gives the ratio of the adjacent side to the hypotenuse in a right-angled triangle.
The arctan function is denoted as arctan(x) or tan⁻¹(x), whre x is the value of the tangent of the angle. For example, if the tangent of an angle is 0.5, then the arctan of 0.5 is the angle whose tangent is 0.5.
In contrast, the cos function is denoted as cos(x) and gives the ratio of the adjacent side to the hypotenuse of a right-angled triangle. For example, if the angle of a right-angled triangle is 30 degrees and the length of the adjacent side is 3 units, and the length of the hypotenuse is 5 units, then the cos of 30 degrees is 3/5 or 0.6.
Arctan and cos are two different trigonometric functions that serve different purposes. Arctan gives the angle whose tangent is a given number, while cos gives the ratio of the adjacent side to the hypotenuse of a right-angled triangle.
Difference Between Arctan and ArcCot
The short answer is no, arctan and arccot are not the same. While both are inverse trigonometric functions, they have different definitions and properties.
Arctan, also known as inverse tangent, is the inverse function of the tangent function. It is denoted as atan(x) or tan⁻¹(x). Arctan takes as input a ratio of two sides of a right triangle and outputs the angle whose tangent is that ratio. In other words, if y = tan(x), then x = atan(y).
On the other hand, arccot, also known as inverse cotangent, is the inverse function of the cotangent function. It is denoted as acot(x) or cot⁻¹(x). Arccot takes as input a ratio of two sides of a right triangle and outputs the angle whose cotangent is that ratio. In other words, if y = cot(x), then x = acot(y).
While arctan and arccot are related, they are not the same function. In fact, they are complementary functions, meaning that arctan(x) + arccot(x) = π/2 for all x. This can be seen by considering the unit circle, whee the tangent and cotangent are defined as the y/x and x/y coordinates, respectively, of the point where the line passing through the origin and a given angle intersects the circle.
To summarize:
– Arctan is the inverse function of the tangent and is denoted as atan(x) or tan⁻¹(x).
– Arccot is the inverse function of the cotangent and is denoted as acot(x) or cot⁻¹(x).
– Arctan and arccot are complementary functions, meaning that arctan(x) + arccot(x) = π/2 for all x.
The Relationship Between Arctan and Inverse Tan
Arctan is the same as the inverse tangent function, often denoted as tan-1. The arctan function is the inverse of the tangent function, which takes an angle as input and returns the ratio of the length of the opposite side to the adjacent side of a right triangle. The arctan function, on the other hand, takes a ratio as input and returns the angle whse tangent is that ratio.
It is important to note that the arctan function is different from the cotangent function, which is the inverse of the tangent’s reciprocal, or 1/tan. The arctan function is commonly used in trigonometry, calculus, and other mathematical disciplines, and is often used to solve problems involving angles or ratios of sides in right triangles.
Here are some key points to summarize:
– Arctan and inverse tan refer to the same function.
– Arctan is the inverse of the tangent function, and takes a ratio as input to return an angle.
– Arctan is not the same as the cotangent function, which is the inverse of the tangent’s reciprocal.
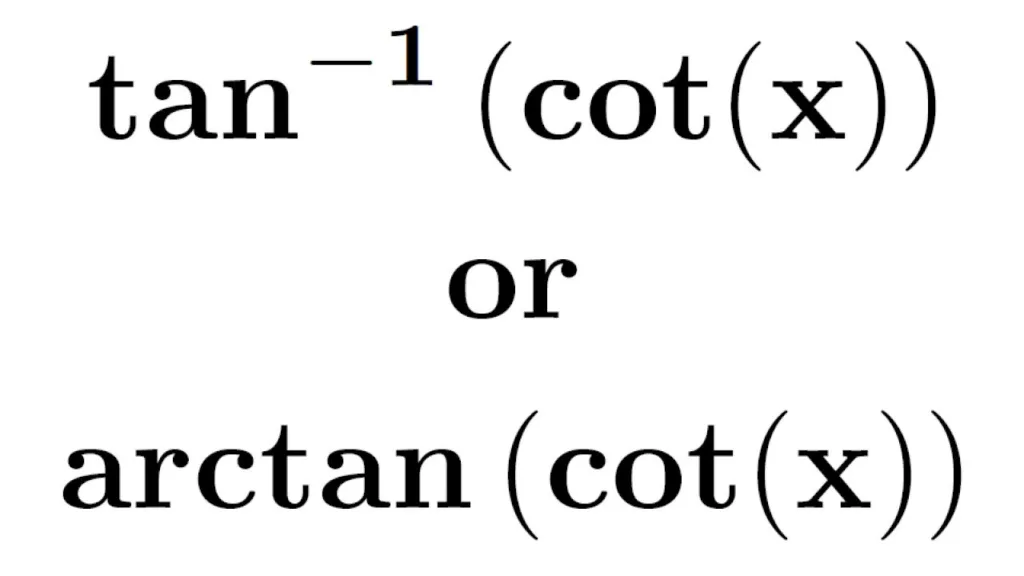
Conclusion
Arctan or the inverse tangent function is an important mathematical concept. It is used to determine the angle between the hypotenuse and the base of a right-angled triangle, given the values of the perpendicular and the base. The formula for arctan is θ = tan-1(Perpendicular / Base).
Arctan is just one of the six inverse trigonometric functions, the others being arcsin, arccos, arccsc, arcsec, and arccot. These functions are essential in many areas of mathematics, physics, and engineering, where they are used to solve complex problems involving angles and triangles.
It is worth noting that the inverse trigonometric functions have certain limitations and restrictions. For instance, the domain of the arctan function is limited to values between -π/2 and π/2 radians or -90° and 90°. Therefore, it is important to understand the limitations and restrictions of these functions before usig them in calculations.
Arctan is a crucial concept in trigonometry and mathematics in general. Its applications are numerous, and its importance cannot be overstated. By understanding the formula and limitations of arctan, we can solve many problems related to angles and triangles in various fields of study.
