A straight line is one of the most basic and fundamental concepts in mathematics. It is a geometric shape that extends infinitely in both directions and is made up of an infinite number of points. Straight lines are used in a variety of mathematical applications, including geometry, trigonometry, and calculus. One of the most important questions related to straight lines is whether or not they represent a function.
In mathematics, a function is a relation between a set of inputs and a set of possible outputs with the property that each input is related to exactly one output. This means that for every value of x, thee is only one value of y. If a graph of a straight line has only one output y for each input x, then it is considered a function.
However, there is one exception to this rule. A vertical line cannot be a function because it has multiple outputs for the same input. This is because a vertical line has an undefined slope and passes through an infinite number of points with the same x-coordinate. Therefore, it is impossible to assign a unique value of y to each value of x.
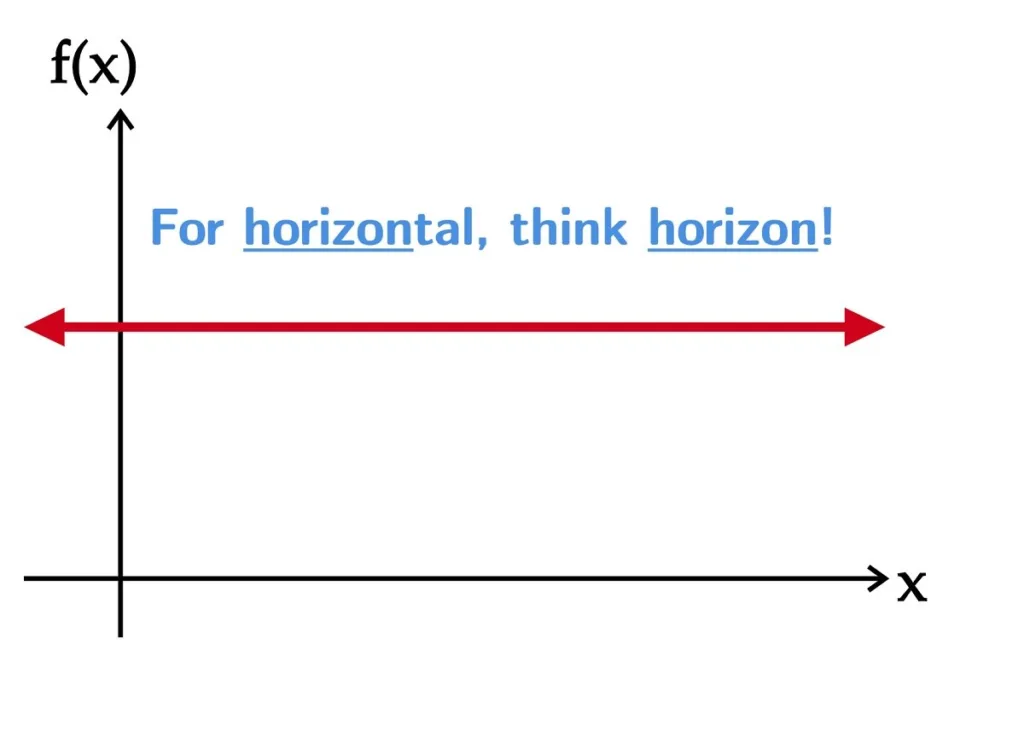
On the other hand, a horizontal line is a function. This is because it has a slope of zero and passes through an infinite number of points with the same y-coordinate. For every value of x, there is only one value of y, which is the y-coordinate of the points on the line.
In general, almost all straight lines are functions because they pass the vertical line test. The vertical line test is a method used to determine if a graph represents a function. It involves drawing a vertical line through the graph and seeing if it intersects the graph in more than one point. If it does, then the graph is not a function. If it does not, then the graph is a function.
A straight line can be a function or not depending on its orientation. A vertical line is not a function, while a horizontal line and almost all other straight lines are functions. This concept is important in mathematics and is used in a variety of applications.
Are Vertical Lines a Function?
When it comes to determining whether a graph represents a function, there are certain criteria that must be met. One of the key requirements is that for every input value, there must be only one corresponding output value. In other words, no two input values can lead to the same output.
With this in mind, we can consider the case of straight vertical lines. A vertical line is one that goes straight up and down, with no horizontal component. If we were to plot such a line on a graph, we would see that for any givn x-value, there are an infinite number of y-values that could be associated with it. This violates the requirement of a function, which demands that there be only one y-value for each x-value.
Therefore, we can conclude that straight vertical lines are not functions. It is important to note, however, that this does not mean that all vertical lines are non-functions. If a line has a horizontal component as well as a vertical one, it can still be a function as long as it meets the other criteria for functions.
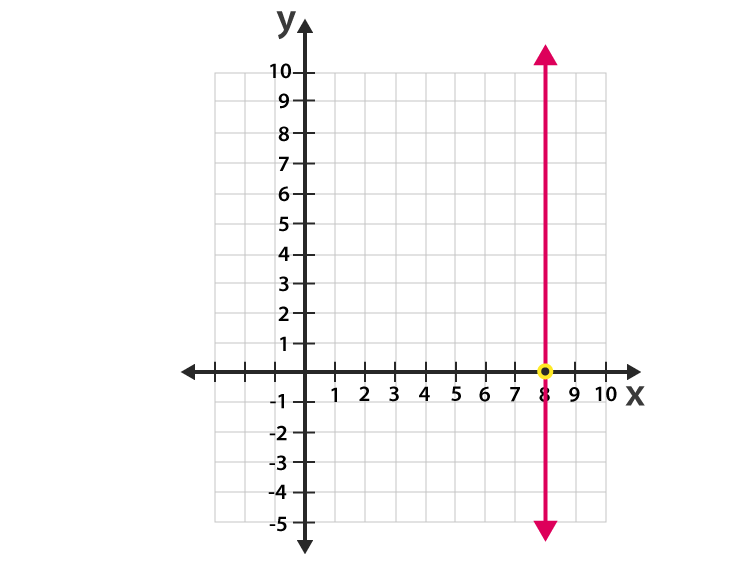
Is a Straight Horizontal Line a Function?
In mathematics, a function is a relation between a set of inputs and a set of possible outputs, with the property that each input is related to exactly one output. Therefore, for a graph to represent a function, each input (or x-coordinate) must have exactly one corresponding output (or y-coordinate).
A straight horizontal line, such as y = 3, violates this property. For any input value, the output value is always 3. This means that multiple input values are associated with the same output value, which violates the definition of a function.
It is important to note, however, that a horizontal line can be the graph of a function if it is restricted to a crtain domain. For example, the function f(x) = 3, defined only for x values between 1 and 5, would be represented by a horizontal line on the interval [1, 5].
A straight horizontal line is not a function, but it can be the graph of a function if it meets the criteria of having a unique output for each input within a restricted domain.
Is a Straight Line a Function?
A straight line is not aways a function, as there are some cases where a vertical line cannot represent a function. This is because a function can only have one output value for each input value, and a vertical line can intersect a graph in more than one point, violating this rule.
However, most linear equations do represent functions, as they pass the vertical line test. The vertical line test is a way to check if a graph represents a function or not. If any vertical line intersects the graph in more than one point, then the graph does not represent a function.
While some straight lines may not represent functions, most linear equations do represent functions. It is important to use the vertical line test to determine whether a graph represents a function or not.
Is Any Line a Function?
In the context of the x-y plane, a line can be represented as a function if it satisfies a specific condition. A function is a relation betwen two variables, x and y, where each value of x is associated with only one value of y. If we consider a line in the x-y plane, it can be represented by an equation of the form y = f(x) = mx + b, where m is the slope of the line and b is the y-intercept.
However, there is one type of line that cannot be represented as a function in the x-y plane, and that is a vertical line. A vertical line can be represented by an equation of the form x = c, where c is a constant. The reason why a vertical line cannot be represented as a function is that for any value of x, there are multiple values of y that satisfy the equation x = c.
To summarize, any line in the x-y plane can be represented as a function, except for a vertical line, which cannot be represented as a function.
Conclusion
Straight lines play a fundamental role in mathematics and are essential in understanding the concept of functions. While not all straight lines are considered functions, the vast majority of them are, and they can be expressed in the form y=f(x)=mx+b. The slope of the line (m) and the y-intercept (b) provide essential information about the graph and its behavior. The study of straight lines extends beyond mathematics and is relevant in various fields such as physics, engineering, and economics. Understanding the properties and behavior of straight lines is crucial in solving real-world problems and making informed decisions.
