When it comes to comparing fractions, it can sometimes be a bit tricky to determine which one is larger. However, with a little bit of knowledge and practice, you can easily compare fractions and determine which one is bigger. In this article, we will answer the question of whether 3/8 is bigger than 1/4.
First, let’s take a look at the denominators of these two fractions. The denominator is the number on the bottom of the fraction, which tells us into how many equal parts the whole is divided. In this case, the denominator of 3/8 is 8, while the denominator of 1/4 is 4.
Now, let’s consider the numerators of these two fractions. The numerator is the number on the top of the fraction, which tells us how many of those equal parts we are dealing with. In this case, the numerator of 3/8 is 3, while the numerator of 1/4 is 1.
So, which one is bigger? The answer is 3/8. This is because 3/8 represents three out of eight equal parts, while 1/4 represents only one out of four equal parts. In other words, 3/8 is a larger fraction because it represents a larger portion of the whole.
To make this concept easier to understand, let’s use a visual example. Imagine you have a pizza that is divided into eight equal slices. If you take three of those slices, you woud have three out of eight slices, or 3/8 of the pizza. Now, imagine you have a different pizza that is divided into four equal slices. If you take one of those slices, you would have one out of four slices, or 1/4 of the pizza. Which pizza has more slices? The first pizza, with its eight slices, has more slices than the second pizza, which only has four slices. Similarly, 3/8 is a larger fraction than 1/4 because it represents a larger portion of the whole.
3/8 is bigger than 1/4. When comparing fractions with different denominators, it is important to convert them to a common denominator before making the comparison. However, when two or more fractions have the same denominator, you can compare them by looking at their numerators. The larger the numerator, the larger the fraction. With a little practice, you can easily compare fractions and determine which one is bigger.
Comparing the Sizes of ¼ and ¾
When comparing fractions, it is important to conider both the numerator and denominator. The numerator represents the number of parts we have, while the denominator represents the total number of parts that make up a whole.
In the case of 1/4 and 3/4, we can see that they have the same denominator, which is 4. This means that they are parts of the same whole, which is divided into four equal parts.
To determine which fraction is bigger, we need to look at their numerators. The numerator of 1/4 is 1, while the numerator of 3/4 is 3. This means that 3/4 represents a larger amount than 1/4, as it has three parts out of four, while 1/4 has only one part out of four.
3/4 is bigger than 1/4. We can remember this by noting that the larger the numerator, the larger the fraction.
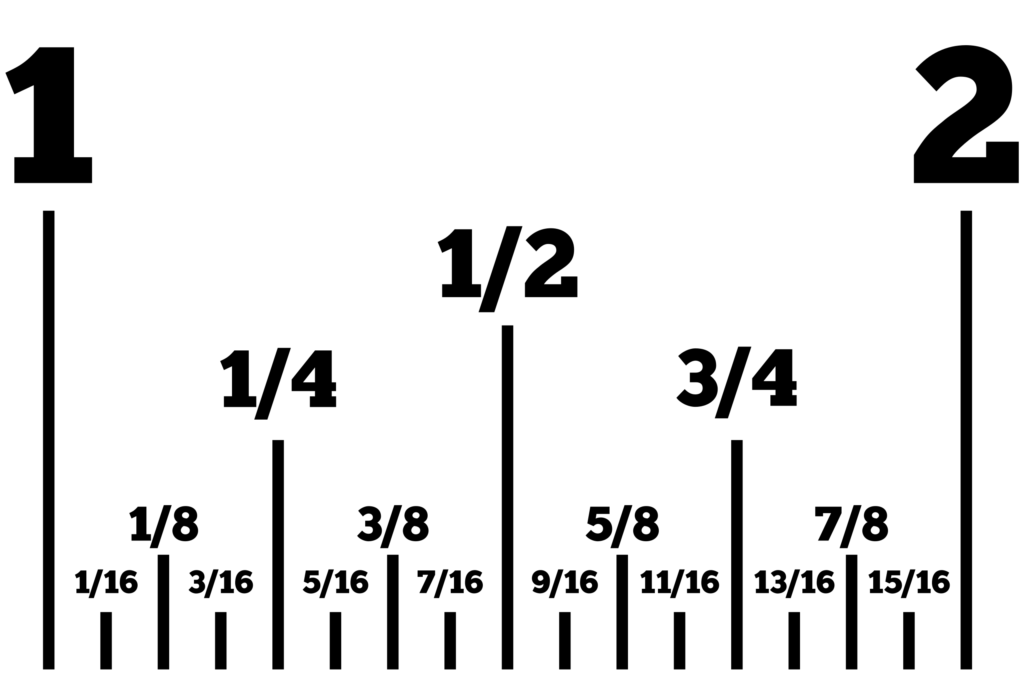
Comparing the Sizes of 1/8 Inch and 1/4 Inch
When it comes to measuring lengths, fractions are commonly used to indicate smaller units of measurement. One eighth (1/8) inch and one fourth (1/4) inch are both fractions of an inch. However, it is important to note that one fourth is a larger fraction than one eighth.
To understand this better, we can divide one inch into eight equal parts. Each of these parts would be 1/8 of an inch. Now, if we divide one inch into four equal parts, each of these parts would be 1/4 of an inch. Therefore, one fourth of an inch is larger than one eighth of an inch.
To put it in a different way, if we were to compare the two fractions, we can convert them to a common denominator. In this case, the common denominator would be 8. One fourth of an inch is equivalent to 2/8 of an inch, whch is larger than 1/8 of an inch.
When measuring lengths in inches, one fourth of an inch is larger than one eighth of an inch.
Conclusion
When comparing fractions, the denominator plays a crucial role. If two or more fractions have the same denominator, we can compare them by looking at their numerators. In the case of 3/8 and 1/4, we can see that both fractions have different denominators, so we need to convert them to a common denominator. By doing so, we get 3/8 and 2/8, which shows us that 3/8 is indeed larger than 1/4. It is essential to remember that the larger the numerator, the larger the fraction, but we must always consider the denominator as well when comparing fractions.
