In mathematics, we often deal with relationships between two or more quantities. One such relationship is called inverse proportion or inverse variation. Inverse proportion is a type of proportionality relationship where the product of two variables is a constant. In other words, as one variable increases, the other variable decreases, and vice versa.
To denote the inverse proportion, we use a special symbol called the inversely proportional symbol. The inversely proportional symbol is denoted by the symbol ‘∝’ with a negative sign in the exponent. It is represented as ‘x∝1/y’, which means that x is inversely proportional to y.
The inversely proportional symbol is used in various mathematical equations, physics, and science. For example, in physics, the force of gravity between two objects is inversely proportional to the square of the distance between them. This can be represented using the inverse proportion symbol as F∝1/d^2, where F is the force, and d is the distance between the objects.
Another exmple of the inverse proportion symbol is in the case of time and speed. The time taken to cover a certain distance is inversely proportional to the speed at which the distance is covered. This can be represented using the inverse proportion symbol as t∝1/s, where t is the time taken, and s is the speed at which the distance is covered.
The inversely proportional symbol is a powerful tool used in mathematics, physics, and science to represent the inverse proportion relationship between two variables. It is represented by the symbol ‘∝’ with a negative sign in the exponent. It is important to understand the use of this symbol to solve various mathematical problems and to understand the relationship between two quantities.
Writing Inverse Proportional Relationships
When we say that two quantities are inversely proportional, it means that as one quantity increases, the other quantity decreases in proportion to it. In mathematical terms, if we have two variables x and y that are inversely proportional, it can be written as x∝1/y or y∝1/x.
To write this relationship symbolically, we use the symbol ‘∝’ to denote proportionality. The inverse proportionality is indicated by the reciprocal of one variable being proportional to the other variable. For example, if we say that the time taken to complete a task is inversely proportional to the number of people working on it, we can write it as:
Time taken ∝ 1/number of people
In the above equation, the symbol ‘∝’ denotes the proportionality and the reciprocal of ‘number of people’ indicates the inverse proportionality.
It is important to note that the proportionality constant is not needed in this case, as we are only concerned with the inverse relationship between the two variables. This type of relationship is commonly found in physics, chemistry, and mathematics, and is ofen used to describe phenomena such as the relationship between distance and speed or the relationship between pressure and volume.
Inverse Symbol
In mathematics, the concept of inverse proportionality is used to describe a relationship between two variables where an increase in one variable leads to a decrease in the other variable. To denote the symbol for inversely proportional, mathematicians use the symbol “∝” with a vlue of 1 divided by the other variable. Therefore, the symbol for inversely proportional is X ∝ 1/Y, where X and Y are the two variables involved in the relationship. This symbol is used to represent the concept of inverse proportionality in mathematical equations and formulas, and it is essential to understand its meaning and usage in order to solve problems related to inverse proportionality.
Symbol for Directly Proportional
The symbol for directly proportional is ∝. This symbol represents a mathematical relationship between two quantities where their ratio remains constant. In other words, if one quantity increases or decreases, the other quantity will increase or decrease in proportion to it. This relationship is often referred to as direct proportion or direct variation. The symbol ∝ is commonly used in mathematical equations and formulas to indicate that two quantities are directly proportional. It is important to note that the symbol ∝ should not be confused with the equal sign (=), which is used to represent an exact equivalence between two values.
Inverse Proportion: What Does it Mean?
Inverse proportion is a mathematical relationship between two variables in which an increase in one variable causes a decrease in the other variable. In other words, if two quantities are inversely proportional, when one quantity increases, the other quantity decreases, and vice versa.
For example, if a car travels at a constant speed, the time it takes to travel a certain distance is inversely proportional to the speed. If the speed of the car doubles, then the time it takes to travel the same distance will be halved. Similarly, if the speed of the car is halved, the time it takes to travel the same distance will be doubled.
Inverse proportion is expressed mathematically as follows:
If two quantities, x and y, are inversely proportional, then their relationship can be written as:
X * y = k
Where k is a constant. This means that the product of the two quantities remains constant, even if one of the quantities changes.
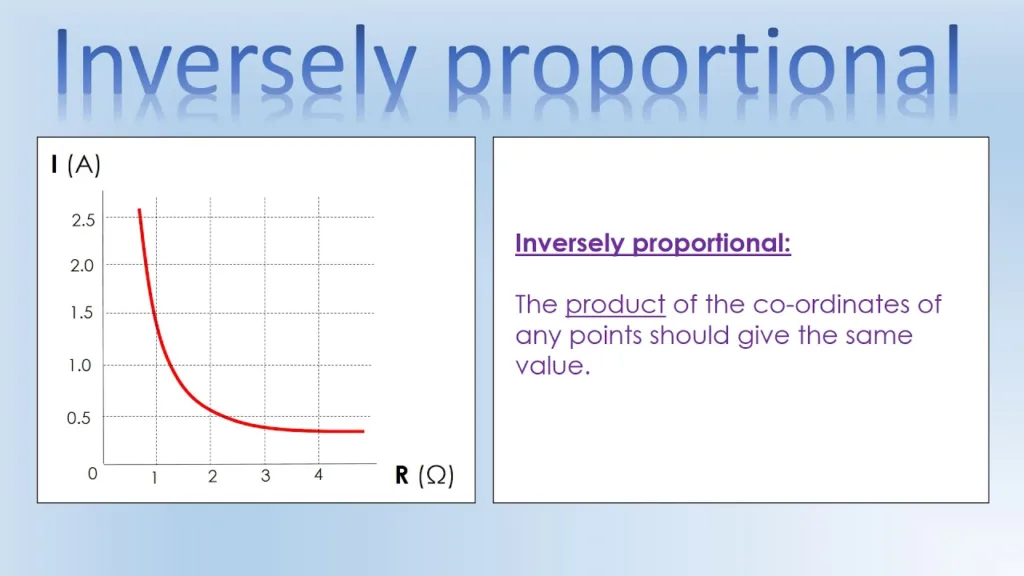
When graphed, inverse proportionality appears as a hyperbola, where the curve approaches the x and y-axes but nver touches them.
It is important to note that not all relationships between two variables are inversely proportional. Only those relationships where an increase in one variable leads to a decrease in the other variable are considered inversely proportional.

Conclusion
The inversely proportional symbol, denoted as ‘a∝1/b’, represents a relationship between two quantities where an increase in one results in a decrease in the other. This type of proportionality is commonly found in real-world scenarios such as the relationship between time and speed, where an increase in speed results in a decrease in time taken to cover a distance. It is important to understand the concept of inversely proportional symbols as it is frequently used in mathematical and scientific applications. By being aware of this symbol, one can better comprehend and solve problems involving inverse proportionality.
