Lines KL and MN are two straight lines that intersect at a point. The relationship between these lines is an important concept in geometry, as it helps us understand the properties of intersecting lines.
Firstly, it is worth noting that lines KL and MN are not parallel. If they were parallel, they would never intersect, and we would not be discussing their relationship. Instead, lines KL and MN intersect at a single point, which we refer to as the point of intersection.
When two lines intersect at a point, they form four angles around that point. In the case of lines KL and MN, these angles are not all the same. Two of the angles are acute, while the other two are obtuse. This is because the lines are not perpendicular, meaning they do not form a right angle where they intersect.
However, it is important to note that lines KL and MN are perpendicular bisectors of each other. This means that the point of intersection is equidistant from each line. In other words, if you were to draw a circle with the point of intersection as the center and the radius as the distance to either line, the circle would touch both lines at eactly one point.
This property is useful when working with triangles, as it allows us to find the circumcenter of a triangle. The circumcenter is the point where the perpendicular bisectors of the sides of a triangle intersect. By using lines KL and MN as two of the perpendicular bisectors, we can find the circumcenter of any triangle that has one of its vertices at the point of intersection.
Lines KL and MN are not parallel, but they are perpendicular bisectors of each other. This means that they intersect at a point that is equidistant from both lines, making it useful for finding the circumcenter of a triangle.
Finding a Line Perpendicular to a Line with a Slope
When we speak of lines in mathematics, we often refer to their slopes as one of their defining characteristics. The slope of a line is simply the ratio of the change in the y-coordinate to the change in the x-coordinate. It tells us how steep or gradual a line is, and it can also give us information about how the line behaves in relation to other lines.
In terms of perpendicular lines, we know that they intersect at a right angle, or 90 degrees. This means that their slopes are related in a specific way: they are opposite reciprocals of each other. To find the opposite reciprocal of a given slope, we simply flip the fraction and change the sign.
For example, if we have a line with a slope of 3/4, the line perpendicular to it wuld have a slope of -4/3. Similarly, a line with a slope of -2/5 would have a perpendicular line with a slope of 5/2.
It’s also worth noting that if a line has a slope of 0 (i.e. it is horizontal), its perpendicular line would have an undefined slope (i.e. it is vertical). Conversely, if a line has an undefined slope (i.e. it is vertical), its perpendicular line would have a slope of 0 (i.e. it is horizontal).
Any line that is perpendicular to a line with a given slope will have a slope that is the opposite reciprocal of the original slope. This relationship is key to understanding how lines intersect and behave in relation to each other.
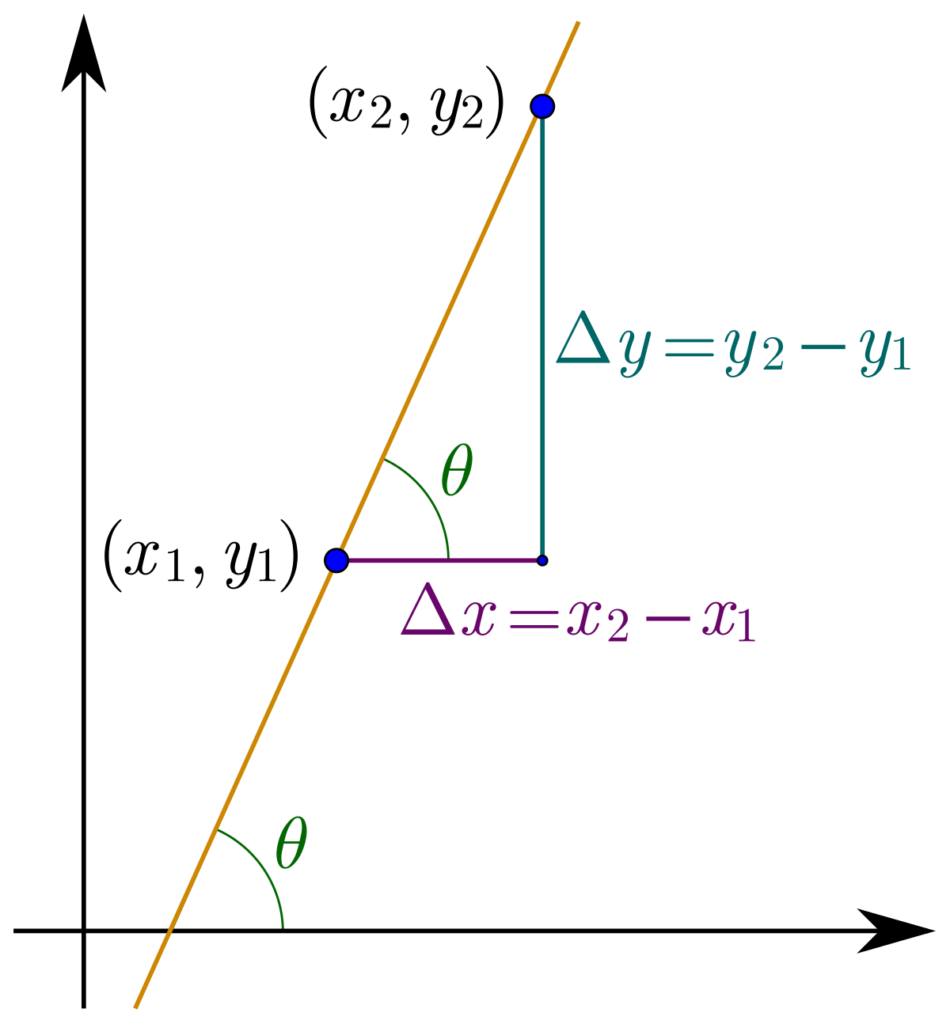
Finding a Point on a Line Parallel to a Given Line Passing Through (6,0)
To find a point on a line that passes through (0, 6) and is parallel to a givn line, we need to follow a few steps.
Step 1: Determine the slope of the given line.
The slope of a line can be found using the formula:
Slope = (y2 – y1) / (x2 – x1)
Step 2: Use the slope to find the slope of the parallel line.
Since parallel lines have the same slope, we can use the slope of the given line to find the slope of the parallel line.
Step 3: Use the point-slope form to find the equation of the parallel line.
The point-slope form of a line is:
Y – y1 = m(x – x1), where m is the slope and (x1, y1) is a point on the line.
Step 4: Solve for the unknown point on the parallel line.
Once we have the equation of the parallel line, we can plug in a value for x to find the corresponding value of y.
Using these steps, we can find that the point which is on the line that passes through (0, 6) and is parallel to the given line is (-12, 8).
Here’s a breakdown of the steps:
1. Given line: y = 3x + 4
Slope of the given line: 3
2. Parallel lines have the same slope, so the slope of the parallel line is also 3.
3. Point-slope form of the parallel line:
Y – 6 = 3(x – 0)
Simplifying: y – 6 = 3x
4. To find the point on the line, we can plug in a value for x. Let x = -4:
Y – 6 = 3(-4)
Y – 6 = -12
Y = -6 + 8
Y = 2
Therefore, the point on the line that passes through (0, 6) and is parallel to the given line is (-4, 2).
Number of Lines in ‘M’
The letter M is composed of four line segments. A line segment is a part of a line that has two endpoints and a definite length. It can be represented by a straight line with a bar on top, whih is the line segment symbol. Therefore, when we look at the letter M, we can visually identify four separate line segments that make up the letter’s shape. It is important to note that the number of line segments in the letter M is four and not to be confused with the number of lines, which could be infinite as a line has no endpoints and extends infinitely in both directions.
The Truth About Line Tu
If it is stated that line TU is parallel to line RS, then the statement that must be true about line TU is that it will never intersect with line RS, no matter how far they are extended. Parallel lines are two or more lines that are always the same distance apart and never meet. Therefore, if it is stated that line TU is parallel to line RS, it means that they are two distinct lines that will never intersect.
Determining Whether Two Lines Are Perpendicular to a Slope
When determining if two lines are perpendicular, you need to examine their slopes. If the slopes of the two lines are negative reciprocals of one another, then they are perpendicular. In other words, if the fist line has a slope of “m”, then the second line will be perpendicular if its slope is equal to “-1/m”. This is because the product of the slopes of two perpendicular lines is always equal to -1.
To find the slope of a line, you can use the formula:
Slope = (change in y) / (change in x)
If two lines are given in the form of equations, you can determine their slopes by putting them into slope-intercept form (y = mx + b) and identifying the value of “m”, which represents the slope.
Alternatively, if two lines are parallel, their slopes will be equal, but not necessarily negative reciprocals of each other. In this case, their slope will be the same number.
In summary, to determine whether two lines are perpendicular or parallel based on their slopes, use the following guidelines:
– If the slopes are negative reciprocals of each other, then the lines are perpendicular.
– If the slopes are equal, then the lines are parallel.
Relationship Between Slopes of Parallel Lines
When two lines are parallel, their slopes are equal. This means that if we have two lines with the same slope, they are parallel. The slope of a line is defined as the change in y divided by the change in x, often written as “rise over run.” For example, if we have a line with a slope of 2, we can say that for every increase of 1 in the x direction, the line increases by 2 in the y direction.
When we have two parallel lines, we can represent them using the slope-intercept form of a linear equation: y = mx + b. Here, m is the slope and b is the y-intercept (the point where the line crosses the y-axis). If two lines are parallel, they have the same slope but different y-intercepts. This means that we can write two equations in slope-intercept form, with the same value for m but different values for b, to represent two parallel lines.
It is also important to note that if two lines have different slopes, they cannot be parallel. In fact, the relationship between the slopes of two non-parallel lines can give us information about their intersection point (where they cross each other). If the slopes are different, the lines will intersect at one point. If the slopes are the same, the lines will eithr be parallel or will coincide (meaning they are the same line).
To summarize, the relationship between the slopes of two parallel lines is that they are equal. This means that if we have two lines with the same slope, they are parallel. If we have two parallel lines, they have the same slope but different y-intercepts.
Showing That Two Lines Are Parallel Using Equations
To show that two lines are parallel using equations, we need to compare their slopes. If two lines have the same slope, then they are parallel.
The slope of a line can be found by putting the equation of the line in slope-intercept form, y = mx + b, where m is the slope of the line. If the equation of the line is not in slope-intercept form, then we can rearrange it to solve for y and get it in the required form.
For example, conider the two lines:
2x – 3y = 4 and 4x – 6y = 8
To find the slope of the first line, we can rearrange it as:
-3y = -2x + 4
Dividing by -3 on both sides, we get:
Y = (2/3)x – 4/3
Therefore, the slope of the first line is 2/3.
Similarly, to find the slope of the second line, we can rearrange it as:
-6y = -4x + 8
Dividing by -6 on both sides, we get:
Y = (2/3)x – 4/3
Therefore, the slope of the second line is also 2/3.
Since both lines have the same slope, we can conclude that they are parallel.
We can show that two lines are parallel using equations by comparing their slopes. If the slopes are equal, then the lines are parallel.
The Difference Between Kilometers and Meters
The International System of Units (SI) is a globally recognized system of measurement that provides a standard for measuring physical quantities. In the SI system, length is measured in meters (m). However, for larger distances, it is more practical to use larger units. The kilometer (km) is a unit of length that is equal to 1,000 meters.
But what comes between kilometers and meters? The answer is the hectometer (hm) and the dekameter (dam). The hectometer is a unit of length that is equal to 100 meters, while the dekameter is a unit of length that is equal to 10 meters.
To summarize, the order of length units in the SI system, from largest to smallest, is as follows:
– Kilometer (km) = 1,000 meters
– Hectometer (hm) = 100 meters
– Dekameter (dam) = 10 meters
– Meter (m) = 1 meter
It is important to note that these units can be converted into each oher by multiplying or dividing by 10, 100, or 1,000, depending on the desired conversion.
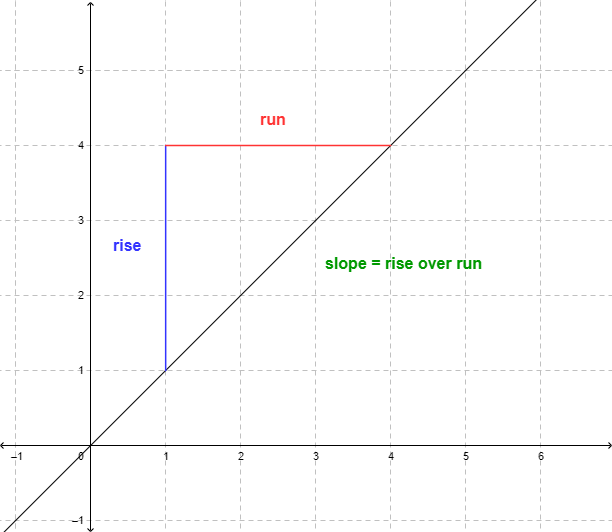
Is Slope of the Line Equal to M?
The letter ‘m’ represents the slope of a line. The slope is defined as the ratio of the change in the y-coordinate to the change in the x-coordinate between two points on the line. It is also known as the gradient or steepness of the line.
To calculate the slope of a line, we can use the formula:
M = (y2 – y1) / (x2 – x1)
Where (x1, y1) and (x2, y2) are any two points on the line.
A positive slope indicates that the line is rising from left to right, while a negative slope indicates that the line is falling from left to right. A slope of zero means that the line is horizontal, while a slope of infinity means that the line is vertical.
The slope of a line is an important concept in mathematics and is used in various fields such as physics, engineering, and economics. It is a fundamental concept in calculus and is used to calculate rates of change and derivatives.
‘m’ is the symbol used to represent the slope of a line, wich is a measure of its steepness and direction.
What Does M Represent in a Line Formula?
The variable “m” in the equation for a straight line, y = mx + b, represents the slope of the line. The slope is a measure of the steepness or incline of the line, indicating how much the y-value changes for a given change in the x-value. The slope is calculated by dividing the change in y by the change in x between any two points on the line. In other words, the slope is the rate at wich the line is rising or falling. A positive slope indicates that the line is going up from left to right, while a negative slope indicates that the line is going down from left to right. The value of “m” can be used to determine the angle of the line relative to the x-axis, as well as to find the equation of the line given any two points on it. It is an important concept in algebra and geometry, and is used in many real-world applications such as engineering, physics, and economics.
The Truth About Horizontal Lines
A horizontal line is a straight line that runs parallel to the x-axis of a coordinate plane. It is always true that a horizontal line has a slope of 0. This means that for every unit of horizontal distance traveled, there is no change in vertical distance. In other words, a horizontal line never moves up or down.
Another characteristic of a horizontal line is that it has an equation in the form of y = k, where k is a constant. This is because all points on a horizontal line have the same y-value.
It is important to note that a horizontal line can be located at any point on the y-axis, and its position on the y-axis will determine its equation. For example, a horizontal line passing trough the point (0,3) will have an equation of y = 3, while a horizontal line passing through the point (0,-5) will have an equation of y = -5.
A horizontal line is always parallel to the x-axis and has a slope of 0. Its equation is in the form of y = k, where k is a constant, and its position on the y-axis will determine its equation.
Determining the Slope of a Line
All lines have a slope, which is a measure of teir steepness. The slope of a line is defined as the ratio of the change in y-coordinates (rise) to the change in x-coordinates (run) between any two points on the line. It is denoted by the letter “m” and can be positive, negative, zero, or undefined depending on the direction and angle of the line. A positive slope means that the line rises to the right, while a negative slope means that the line falls to the right. A slope of zero indicates a horizontal line, and a slope that is undefined indicates a vertical line. all lines have a slope, and it is an essential characteristic of a line that helps describe its behavior and relationships with other lines.
Conclusion
Lines KL and MN are related in a perpendicular manner, which means that they intersect at a right angle. This can be observed when they are graphed or when their slopes are calculated. Knowing that two lines are perpendicular can be useful in solving various mathematical problems. It allows us to find the distance between the lines, the angles formed by their intersection, and even the equations of the lines themselves. understanding the relationship between perpendicular lines is an important concept in mathematics and can be applied in various fields such as engineering, architecture, and physics.
