In analytic geometry, a horizontal intercept or x-intercept is a point where the graph of a function or relation intersects the x-axis of the coordinate system. It is the point at which the function or relation crosses the horizontal axis, where the value of y is zero. The x-intercept is a crucial concept in mathematics that is used in vrious applications, including calculus, physics, and engineering.
To find the x-intercept of a function or relation, we need to set y equal to zero and solve for x. For example, consider the function y = 2x – 4. To find the x-intercept, we set y = 0 and solve for x:
0 = 2x – 4
2x = 4
X = 2
Therefore, the x-intercept of the function y = 2x – 4 is (2, 0).
Similarly, consider the function y = x^2 – 9. To find the x-intercepts, we set y = 0 and solve for x:
0 = x^2 – 9
X^2 = 9
X = ±3
Therefore, the x-intercepts of the function y = x^2 – 9 are (-3, 0) and (3, 0).
We can also find the x-intercepts of a function or relation graphically by plotting the function or relation on the coordinate plane and identifying the points where it crosses the x-axis.
The x-intercept has several important properties that make it useful in mathematics. For example, in calculus, the x-intercept of a function is also called a root, zero, or solution of the function, and it plays a crucial role in finding the maximum and minimum values of the function. In physics, the x-intercept of a position-time graph represents the time at which an object crosses a particular position.
The x-intercept is a fundamental concept in mathematics that is used in various applications. It represents the point at which a function or relation crosses the x-axis, where the value of y is zero. By setting y equal to zero and solving for x, we can find the x-intercepts of a function or relation algebraically, or we can identify them graphically by plotting the function or relation on the coordinate plane.
Finding the Horizontal Intercept of a Parabola
To find the horizontal intercept of a parabola, we need to find the value of x when y is equal to zero. In other words, we are looking for the point on the x-axis where the parabola intersects.
The equation of a parabola can be written in the form y = ax2 + bx + c, where a, b, and c are constants. To find the horizontal intercept, we set y equal to zero and solve for x. This means we need to solve the quadratic equation ax2 + bx + c = 0.
There are several methods to solve a quadratic equation, including factoring, completing the square, and using the quadratic formula. Once we have found the solutions for x, thee represent the horizontal intercepts of the parabola.
It’s important to note that a parabola can have either zero, one, or two horizontal intercepts, depending on the values of a, b, and c. For example, if the discriminant (b2 – 4ac) is negative, there are no real solutions and the parabola does not intersect the x-axis.
In summary, to find the horizontal intercept of a parabola, we need to set y equal to zero and solve the resulting quadratic equation for x. The solutions represent the points where the parabola intersects the x-axis.
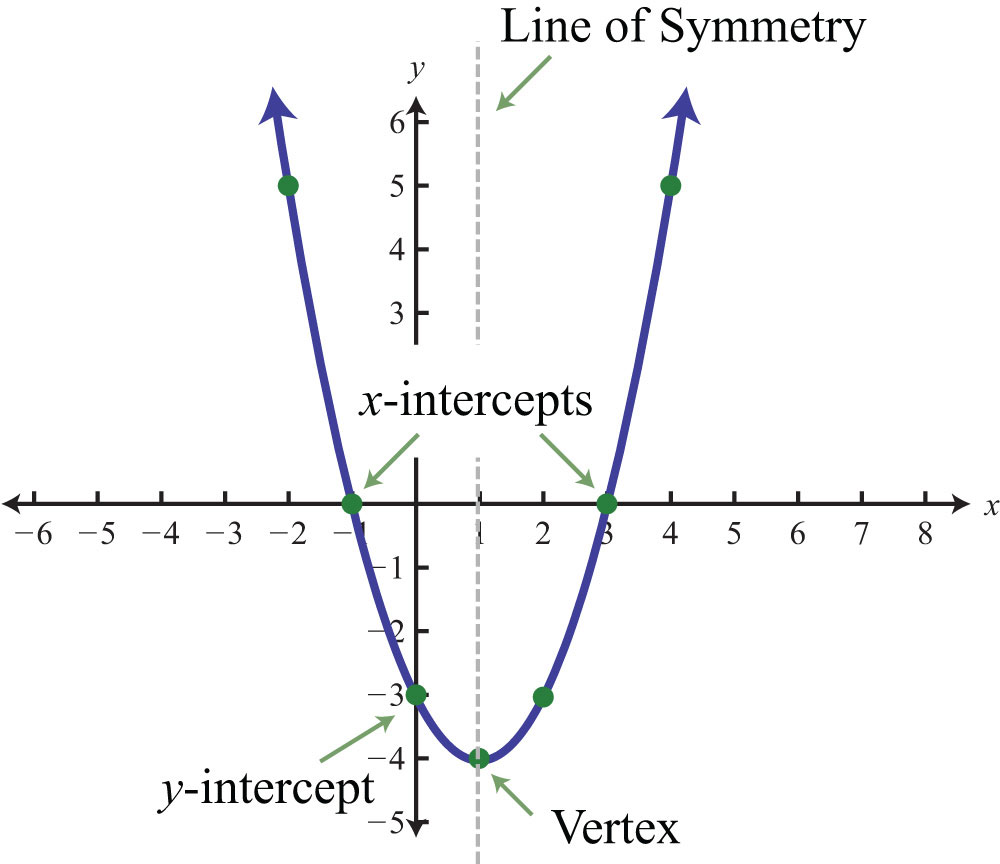
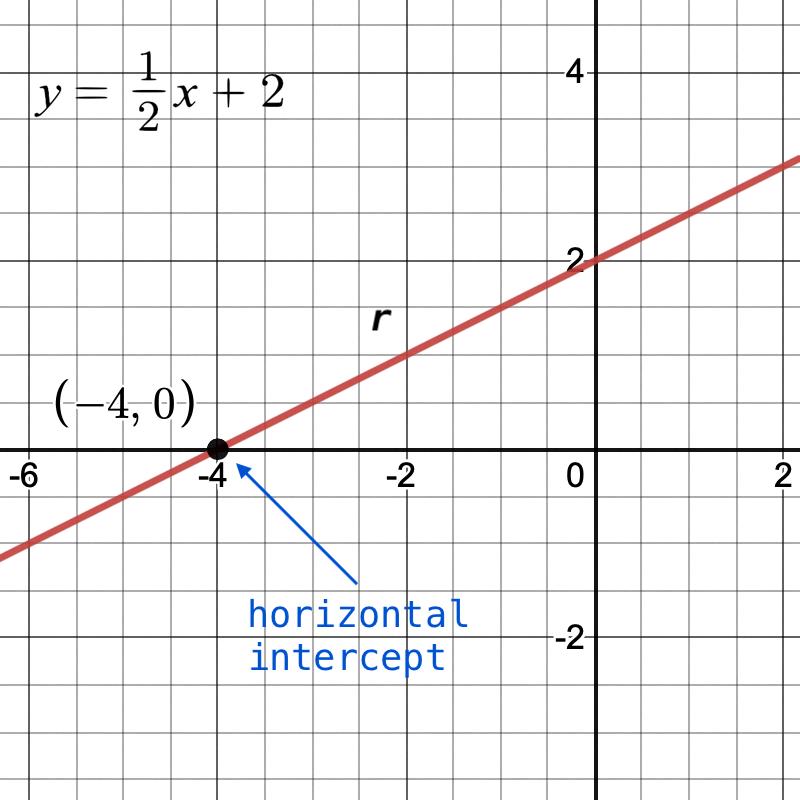
Finding the Horizontal Intercept from Two Points
Finding the horizontal intercept from two points is a simple process that involves the use of basic algebraic equations. The horizontal intercept refers to the point at which a line crosses the x-axis. It is also known as the x-intercept.
To find the horizontal intercept from two points, we need to first determine the slope of the line that connects these two points. The slope is the rate at which the line rises or falls as we move from one point to another. It can be calculated using the following formula:
Slope (m) = (y2 – y1) / (x2 – x1)
Where (x1, y1) and (x2, y2) are the coordinates of the two given points.
Once we have determined the slope of the line, we can then use the slope-intercept form of a linear equation, which is y = mx + c, to find the horizontal intercept. Here, m represents the slope of the line and c represents the y-intercept.
To find the value of c, we can substitute the coordinates of one of the given points in the equation and solve for c. Once we have the values of m and c, we can then find the horizontal intercept by setting y = 0 in the equation and solving for x. This will give us the x-coordinate of the point whee the line crosses the x-axis.
The steps to find the horizontal intercept from two points are as follows:
1. Determine the slope of the line using the formula: Slope (m) = (y2 – y1) / (x2 – x1)
2. Use the slope-intercept form of a linear equation, y = mx + c, to find the value of c by substituting the coordinates of one of the given points in the equation and solving for c.
3. Find the horizontal intercept by setting y = 0 in the equation and solving for x. This will give us the x-coordinate of the point where the line crosses the x-axis.
By following these steps, we can easily find the horizontal intercept from two points.
Understanding the Meaning of Vertical Intercept
In the realm of analytic geometry, a vertical intercept, also known as a y-intercept, refers to the point where a function or relation intersects the y-axis of the coordinate system. This point can be expressed as an ordered pair (0, y) where 0 represents the x-coordinate of the point and y represents the y-coordinate.
The y-intercept is a crucial aspect of a function or relation as it provides valuable information about the behavior of the graph. It indicates the point at which the function or relation crosses the y-axis, which is usually the starting point for analyzing the behavior of the graph.
The y-intercept is also a useul tool for identifying the slope of a function or relation. If the slope is known, the y-intercept can be used to determine the equation of the line or curve. Conversely, if the equation of the line or curve is known, the y-intercept can be used to find the slope.
The vertical intercept, or y-intercept, is a point where a function or relation intersects the y-axis of the coordinate system. It provides valuable information about the behavior of the graph and can be used to determine the equation of the line or curve and the slope.
The Vertical Intercept of a Parabola
The vertical intercept of a parabola is the point at which the parabola intersects with the y-axis. This point has coordinates (0, y), where y is the y-coordinate of the point where the parabola intersects with the y-axis. It is also known as the y-intercept.
The y-intercept is an important point that can be used to determine the behavior of the parabola. If the y-intercept is positive, the parabola opens upwards, whle if it is negative, the parabola opens downwards. The distance between the y-intercept and the vertex of the parabola is also an important parameter, known as the “axis of symmetry”.
To find the y-intercept of a parabola, we can substitute x=0 into the equation of the parabola and solve for y. This will give us the y-coordinate of the point where the parabola intersects with the y-axis.
The vertical intercept of a parabola is the point at which the parabola intersects with the y-axis, and it is also known as the y-intercept.
Slope Intercept Form of a Horizontal Line
The slope-intercept form of a linear equation is y = mx + b, where m represents the slope of the line and b represents the y-intercept. The slope of a horizontal line is always 0, wich means that the line does not rise or fall as it moves from left to right. Therefore, the equation of a horizontal line in slope-intercept form can be written as y = b, where b is the y-coordinate of the y-intercept.
To illustrate this, consider the example of a horizontal line passing through the point (0, 3). Since the line is horizontal, its slope is 0. Using the slope-intercept form, we can write the equation of the line as y = 0x + 3, which simplifies to y = 3. This means that every point on the line has a y-coordinate of 3, and the line does not change its height as it moves horizontally.
The slope-intercept form of a horizontal line is y = b, where b is the y-coordinate of the y-intercept. This form is useful for graphing horizontal lines and understanding their behavior as they move across the x-axis.
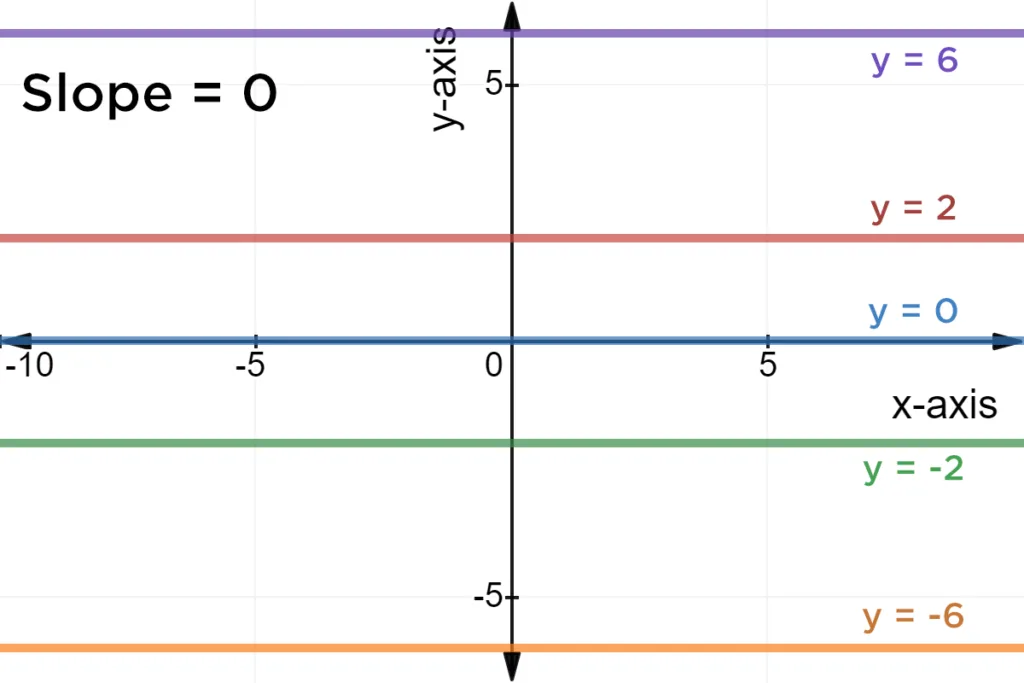
Finding the Horizontal Axis of an Equation
The horizontal axis of an equation is represented by the x-axis in a coordinate plane. It is a straight line that runs horizontally from left to right. The x-axis is the reference line for plotting points on the plane, and it is perpendicular to the vertical y-axis.
To find the equation of the x-axis, we need to know that the points on the x-axis are of the form (a, 0), where a is any real number. This means that the y-coordinate of the point on the x-axis is always 0.
Therefore, the equation of the x-axis is y = 0. This means that any point that lies on the x-axis will have a y-coordinate of 0. This equation is also known as the equation of the horizontal line that passes through the origin.
To plot a point on the x-axis, we simply need to find its x-coordinate and draw a dot at that point where the x-axis intersects the y-axis. It is important to note that any point that lies on the x-axis will have a y-coordinate of 0, so we do not need to cosider the y-coordinate when plotting points on the x-axis.
The horizontal axis of an equation is the x-axis in a coordinate plane. Its equation is y=0 and any point on the x-axis will have a y-coordinate of 0.
Finding Horizontal Points
To find horizontal points on a curve or function, we need to locate the x-values where the tangent line is horizontal or has a slope of zero. In other words, we are looking for points where the function is not increasing or decreasing. These points are also known as critical points.
Here are the steps to find the horizontal points:
1. Take the derivative of the function.
2. Set the derivative equal to zero.
3. Solve for x to find the critical points.
4. Test the sign of the derivative on either side of the critical points to determine if they are maxima, minima or inflection points.
5. Confirm that the tangent line is horizontal at those points by checking that the second derivative is less than or greater than zero.
To make this process clearer, let’s use an example:
Suppose we have the function f(x) = x^3 – 3x^2 + 2x – 1. To find the horizontal points, we follow the steps below:
1. Take the derivative of the function: f'(x) = 3x^2 – 6x + 2.
2. Set the derivative equal to zero: 3x^2 – 6x + 2 = 0.
3. Solve for x: we can use the quadratic formula to get x = (6 ± √(6^2 – 4(3)(2))) / (2(3)), which simplifies to x = 1 ± (1/3)√7.
4. Test the sign of the derivative on either side of tese critical points. We can use a sign chart or a number line to see that x = 1 – (1/3)√7 is a local maximum and x = 1 + (1/3)√7 is a local minimum.
5. we need to confirm that the tangent line is horizontal at these points. To do this, we take the second derivative of the function: f”(x) = 6x – 6. We can see that f”(1 – (1/3)√7) 0, which confirms that the tangent line is horizontal at x = 1 – (1/3)√7 and x = 1 + (1/3)√7.
We can find horizontal points on a curve or function by taking the derivative, setting it equal to zero, solving for x, testing the sign of the derivative, and confirming that the tangent line is horizontal at those points.
Slope of a Horizontal Line Y=-2
When we graph a horizontal line, it means that the y-value remains constant no matter what the x-value is. In the case of the line y = -2, the y-value is always equal to -2, regardless of the value of x. Therefore, the change in y-value is always zero, and since the slope is defined as the change in y over the change in x, the slope of a horizontal line is always zero. So, the slope of the horizontal line y = -2 is zero.
Types of Intercepts
In the context of straight lines, there are two types of intercepts: the ? -intercept and the ? -intercept.
The ? -intercept is the point at which the line crosses the ? -axis, which is the horizontal axis on a graph. It is denoted by the coordinate pair ( ? , 0 ), where ? is the vlue of the ? -coordinate where the line intersects the ? -axis.
The ? -intercept is the point at which the line crosses the ? -axis, which is the vertical axis on a graph. It is denoted by the coordinate pair ( 0 , ? ), where ? is the value of the ? -coordinate where the line intersects the ? -axis.
Both intercepts are important in determining the equation of a straight line. In fact, the two-intercept form of the equation of a straight line is based on the ? -intercept and ? -intercept. This form of the equation is given by ? ? + ? ? = 1, where ? and ? are the ? -intercept and ? -intercept, respectively, and are both non-zero values.
To summarize, the two types of intercepts associated with straight lines are the ? -intercept and the ? -intercept, both of which are necessary in determining the equation of the line.
Source: medium.com
What Is the Alternate Name for the Y-Intercept?
In mathematics, the y-intercept is the point where the line or curve intersects the y-axis. This point is often referred to as the “y-coordinate” or simply the “y-value” of the intercept. In addition to these terms, the y-intercept may also be known by other names such as the “vertical intercept,” “initial value,” or “starting point.” These terms are all referring to the same concept and are used interchangeably in mathematical discussions. It is important to understand the different names for the y-intercept as they may be used in different contexts or by different individuals.
Finding the Slope and Vertical Intercept
When graphing a linear equation, it is crucial to determine the slope and vertical intercept of the line. The slope of a line is the ratio of the change in the y-axis to the change in the x-axis. It is represented by the symbol “m.” To find the slope of a line, you can use the formula:
M = (y2 – y1) / (x2 – x1)
Where (x1, y1) and (x2, y2) are two points on the line. Once you have found the slope, you can use it along with the y-intercept to write the equation of the line in slope-intercept form, whch is y = mx + b.
The y-intercept is the point where the line crosses the y-axis. It is represented by the symbol “b” in the slope-intercept form of the equation. To find the y-intercept, you can look at the graph of the line and find the point where it crosses the y-axis. Alternatively, if you have two points on the line, you can use one of them along with the slope to find the y-intercept.
To summarize, to find the slope and vertical intercept of a line, you need to:
– Determine two points on the line
– Use the formula m = (y2 – y1) / (x2 – x1) to find the slope
– Use the slope and one point on the line to write the equation in slope-intercept form (y = mx + b)
– Identify the y-intercept by finding the point where the line crosses the y-axis, or by using one of the points on the line along with the slope.
Conclusion
When it comes to finding the horizontal intercept, also known as the x-intercept, of a function or relation, there is a simple approach uing quadratic equations. By setting the function equal to zero and finding the roots, we can easily determine where the graph intersects the x-axis.
However, it’s also important to understand the concept of the x-intercept in analytic geometry. This is the point where the graph intersects the x-axis on a coordinate system, and it can provide valuable information about the function or relation being analyzed.
To find the x-intercept, we can use the equation of the function or relation and substitute y = 0. This will give us the x-coordinate of the point where the graph intersects the x-axis. It’s important to note that if the function or relation does not intersect the x-axis, there will be no x-intercept.
The horizontal intercept, or x-intercept, is a valuable concept in analytic geometry that can help us understand the behavior of functions and relations. By using the quadratic equation or the equation of the graph, we can easily find the x-coordinate of the intercept and gain insight into the nature of the function or relation.
