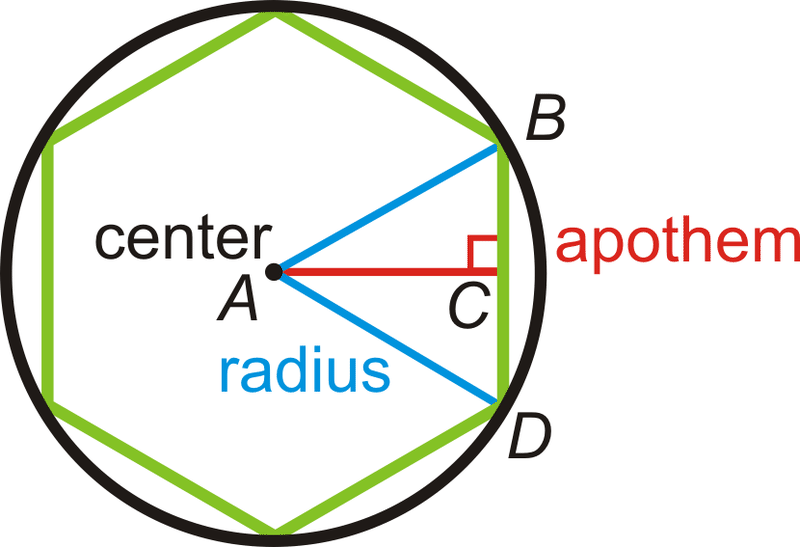
The apothem of a polygon is an important concept in geometry. It is the distance from the center of a polygon to the midpoint of one of its sides. The apothem is a crucial component in the calculation of the area of a polygon. The formula for the apothem of a regular polygon is qute simple.
Formula for Apothem:
The formula for the apothem of a regular polygon is:
A = (s / 2) / tan(π / n)
Where a is the apothem, s is the length of one of the sides of the polygon, and n is the number of sides.
This formula can be used to calculate the apothem of any regular polygon, regardless of the number of sides. It is important to note that the polygon must be regular for this formula to work. A regular polygon has all sides and angles equal.
Example:
Let’s take the example of a regular hexagon. A hexagon has six sides, so n = 6. Let’s say that the length of one of the sides of the hexagon is 8 units.
Using the formula, we can calculate the apothem as follows:
A = (s / 2) / tan(π / n)
A = (8 / 2) / tan(π / 6)
A = 4 / tan(π / 6)
A = 4 / 0.577
A = 6.928 units
Therefore, the apothem of a regular hexagon with a side length of 8 units is 6.928 units.
The apothem is an important component in the calculation of the area of a regular polygon. The formula for the area of a regular polygon is:
A = (1/2) * apothem * perimeter
Where A is the area, apothem is the apothem of the polygon, and perimeter is the perimeter of the polygon.
The apothem can also be used to find the length of the diagonal of a regular polygon. The formula for the length of the diagonal is:
D = s / sin(π / n)
Where d is the length of the diagonal and s is the length of one of the sides of the polygon.
The apothem is an important concept in geometry, and understanding it is crucial for solving problems involving regular polygons. By using the formula for the apothem, we can calculate the apothem of any regular polygon, and use it to solve a variety of geometric problems.
Finding the Apothem
Apothem is a term used in geometry that refers to the distance from the center of a polygon to its sides. It is an important measurement used in determining various properties of polygons, such as their area and perimeter. Finding the apothem of a regular polygon is relatively easy, as it only requires knowing the length of its sides and the number of sides it has. Here are the steps to find the apothem:
Step 1: Determine the length of one side of the polygon.
Step 2: Count the number of sides the polygon has.
Step 3: Use the formula a = s / (2*tan(180/n)) to find the apothem, where a is the apothem, s is the length of one side, and n is the number of sides.
Alternatively, if you know the area and perimeter of the polygon, you can use the formula A = (1/2) aP to find the apothem, where A is the area, P is the perimeter, and a is the apothem.
Finding the apothem of a polygon requires knowing the length of one side and the number of sides it has. You can use the formula a = s / (2*tan(180/n)) or A = (1/2) aP to find the apothem, depending on the inormation you have.

What is the Definition of Apothem in a Pentagon?
In geometry, a pentagon is a five-sided polygon. The apothem of a regular pentagon is defined as the distance from the center of the pentagon to any one of its sides, measured along a line that is perpendicular to that side. The word “apothem” comes from the Greek word “apo” which means “from” and “temnein” which means “to cut”. The apothem of a pentagon is the line that cuts the pentagon in half, dividing it into two congruent triangles.
The apothem of a pentagon is an important geometric property that is used to calculate the area and perimeter of the pentagon. It is also used in various real-life applications such as building construction, engineering, and design.
Here are a few key points to keep in mind about apothems in pentagons:
– The apothem of a pentagon is alays perpendicular to one of its sides.
– The length of the apothem can be calculated using the formula: apothem = (side length) / (2 * tan(180 degrees / 5))
– The area of a regular pentagon can be calculated using the formula: area = (1/2) * (perimeter) * (apothem)
– The perimeter of a regular pentagon can be calculated using the formula: perimeter = 5 * (side length)
The apothem of a pentagon is a line that connects the center of the pentagon to one of its sides. It is an important geometric property that is used to calculate the area and perimeter of the pentagon, and has various real-life applications in fields such as engineering and design.
What is the Definition of Apothem?
Apothem is a term used in geometry to describe the distance from the midpoint of a chord to the center of a circle. More specifically, it represents the perpendicular segment that extends from the center of the circle to the chord. In a regular polygon, the apothem refers to the distance from the center to a side, which is also kown as the inradius of the polygon.
The length of the apothem can be calculated using different formulas, depending on the given information. For instance, in a regular polygon, the apothem can be found by dividing the length of the side by two times the tangent of half the interior angle. Alternatively, it can be calculated by dividing the area of the polygon by half of its perimeter.
The apothem is a crucial component in determining various properties of circles and polygons. For instance, it is used to calculate the area of polygons through the formula A = (apothem x perimeter)/2. It is also used in finding the length of the sagitta, which is the height of an arc above its chord.
The apothem is a geometric term that represents the distance from the center to a side of a regular polygon or the midpoint of a chord to the center of a circle. It is essential in determining various properties of polygons and circles and can be calculated using different formulas, depending on the given information.
What is the Apothem?
The apothem is a geometric term used to describe a line segment that connects the center of a regular polygon to the midpoint of one of its sides. In other words, it is the perpendicular distance from the center of the polygon to one of its edges. The apothem is also equivalent to the radius of the inscribed circle of the polygon, which is a circle that is tangent to all the sides of the polygon.
The apothem is an important concept in geometry because it can be used to calculate varios properties of regular polygons, such as their area and perimeter. Specifically, the area of a regular polygon can be found by multiplying the apothem by half the perimeter, while the perimeter can be found by multiplying the number of sides by the length of each side.
It is important to note that the concept of apothem only applies to regular polygons, which are polygons that have equal side lengths and equal angles between adjacent sides. Some examples of regular polygons include squares, equilateral triangles, and hexagons.
The apothem is a line segment that connects the center of a regular polygon to the midpoint of one of its sides. It is equivalent to the radius of the inscribed circle of the polygon and can be used to calculate various properties of regular polygons.
What is the Apothem of a Polygon?
The apothem of a polygon is a line segment that runs from the center of the polygon to the midpoint of one of its sides, forming a right angle with that side. In other words, the apothem is the perpendicular distance from the center of the polygon to one of its sides. This distance can be calculated using various formulas, depending on the type of polygon in question.
The apothem is an important measurement in geometry, as it can be used to calculate the area of a polygon. Specifically, the area of a polygon can be calculated by multiplying the apothem by half the perimeter of the polygon. This formula is knon as the apothem formula and can be written as:
Area = (apothem x perimeter)/2
The apothem also plays a role in determining the angles of a polygon. For example, the measure of each interior angle of a regular polygon can be calculated using the formula:
Interior angle = 180(n-2)/n
Where n is the number of sides in the polygon. The apothem can be used to find the length of one of the sides in the polygon, which is necessary for calculating the interior angle.
The apothem is a key measurement in polygon geometry that helps to determine both the area and angles of a polygon.
Finding the Apothem and Area
Finding the apothem and area of a regular polygon involves using some specific formulas. The apothem is the perpendicular distance between the center of the polygon and one of its sides. The area is the amount of space inside the polygon.
To find the apothem of a regular polygon, you can use the following formula: a = s / (2 × tan(π/n)), whre a is the apothem, s is the length of one side, n is the number of sides, and π is pi (3.14159…). This formula works for any regular polygon, whether it has three sides (a triangle) or many sides (a decagon, dodecagon, etc.).
To find the area of a regular polygon, you can use the following formula: A = (n × s × a) / 2, where A is the area, n is the number of sides, s is the length of one side, and a is the apothem. This formula works for any regular polygon as well.
Here is a step-by-step guide to finding the apothem and area of a regular hexagon (a six-sided polygon) with a side length of 5:
1. Find the apothem: Using the formula a = s / (2 × tan(π/n)), we get a = 5 / (2 × tan(π/6)) ≈ 4.3301.
2. Find the area: Using the formula A = (n × s × a) / 2, we get A = (6 × 5 × 4.3301) / 2 ≈ 64.9519.
Therefore, the apothem of the regular hexagon is approximately 4.3301 and the area is approximately 64.9519.
Calculating the Apothem and Radius
In geometry, the apothem and radius are two important terms used to describe regular polygons. A regular polygon is a polygon with sides of equal length and angles of equal measure. The apothem and radius are both segments that connect the center of the polygon to other points on the polygon.
The apothem of a regular polygon is a segment that connects the center of the polygon to a midpoint of one of the sides. It is perpendicular to that side and has a length equal to the radius of the inscribed circle of the polygon. The inscribed circle is the largest circle that can be drawn inside the polygon and it is tangent to each of the sides.
The radius of a regular polygon is a segment that connects the center of the polygon to one of the vertices. It is the distance from the center of the polygon to the vertex and it is equal in length to the radius of the circumcircle of the polygon. The circumcircle is the smallest circle that can be drawn arund the polygon and it passes through each of the vertices.
To summarize:
– The apothem connects the center of the polygon to a midpoint of one of the sides and is equal to the radius of the inscribed circle.
– The radius connects the center of the polygon to one of the vertices and is equal to the radius of the circumcircle.
Here are a few additional points to keep in mind:
– The apothem and radius are both important in calculating the area and perimeter of a regular polygon.
– The apothem and radius are only defined for regular polygons, which have all sides and angles equal.
– The apothem and radius are both examples of radii (plural of radius), which are segments that connect the center of a circle to its perimeter.
Is Apothem the Same as Height?
The terms apothem and height are related to polygons, but they refer to two different measurements. The height of a polygon is the perpendicular distance between one of its sides and its opposite side (or between a side and a line parallel to its opposite side). On the oher hand, the apothem of a polygon is the perpendicular distance between its center and one of its sides.
To better understand the difference between these two measurements, let’s take a look at an example. Consider a regular hexagon, which is a polygon with six sides of equal length and six angles of equal measure. If we draw a line segment from the center of the hexagon to one of its vertices, we create a radius of the hexagon. Then, if we draw a perpendicular line from the center of the hexagon to one of its sides, we create an apothem of the hexagon. Finally, if we draw a line segment from one vertex to its opposite vertex, we create a diagonal of the hexagon, which is also a height of the hexagon.
While the height of a polygon is a distance between two parallel or opposite sides, the apothem of a polygon is a distance between its center and one of its sides. Therefore, the apothem and the height are not the same measurement, although they are both important in the study of polygons.
Length of an Apothem
The length of an apothem is a geometric measurement that refers to the distance from the center of a polygon to the midpoint of any of its sides. It is an important measurement for regular polygons, as it is used to calculate the area of the polygon. The apothem is a perpendicular segment that connects the center of the polygon to the midpoint of one of its sides.
To calculate the length of an apothem, you need to know the side length of the polygon and the tangent of half the interior angle at the polygon’s center. The formula for calculating the apothem is as follows:
Apothem = (Side Length)/(2 x Tan(Interior Angle/2))
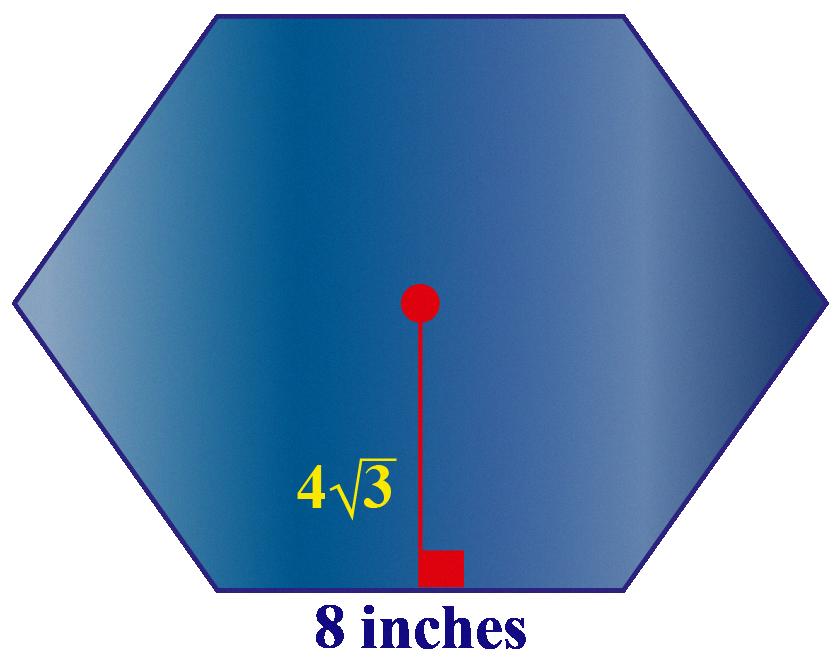
For example, if you have a regular hexagon with a side length of 8 cm, you can calculate the apothem using the formula above. The interior angle of a regular hexagon is 120 degrees, so half the interior angle is 60 degrees. The tangent of 60 degrees is approximately 1.732. Multiplying this by 2 gves you 3.464. Dividing the side length of 8 cm by 3.464 gives you approximately 2.31 cm as the length of the apothem for the regular hexagon.
It is also worth noting that the apothem is a measurement that is only relevant for regular polygons, and not for irregular polygons, which do not have a center point or equal side lengths.
Source: cuemath.com
Is the Apothem Half the Height?
The apothem of a regular polygon is not alays half the height. The height of a polygon is the distance from the base to the opposite vertex or the highest point of the polygon. The apothem, on the other hand, is the distance from the center of the polygon to the midpoint of a side. The relationship between the height and the apothem depends on the shape of the polygon.
In the case of a regular hexagon, the apothem is equal to one-third of the height. This can be seen by drawing the perpendicular from the center of the hexagon to one of the sides, which will create a right triangle. The height of the hexagon is the length of the hypotenuse of this triangle, while the apothem is the length of one of the legs. The other leg is half the length of one side of the hexagon.
Therefore, the apothem of a regular hexagon is given by the formula:
Apothem = (1/2) * (side length) * tan(30°)
Or
Apothem = (1/3) * (height)
It is important to note that this relationship only holds true for regular polygons, where all sides and angles are equal. For irregular polygons, the relationship between the apothem and the height will be different, and will depend on the specific shape of the polygon.
Area of a Polygon Formula
Calculating the area of a polygon can be a challenging task, especially if the polygon in question has an irregular shape. However, for a regular polygon, the formula for calculating its area is relativey straightforward. A regular polygon is a polygon with all sides and angles of equal length and measure, respectively.
The formula for finding the area of a regular polygon is given as:
A = (n/2) * L * R
Where A is the area of the polygon, n is the number of sides in the polygon, L is the length of one side of the polygon, and R is the radius of the inscribed circle.
In other words, to find the area of a regular polygon, you need to know the number of sides, the length of one side, and the radius of the inscribed circle. The inscribed circle is the largest circle that can be drawn inside the polygon, touching each side of the polygon.
To further explain the formula, let’s break it down into its components:
– (n/2): This term represents the number of triangles that make up the polygon. A regular polygon can be divided into n/2 triangles, where n is the number of sides. For example, a hexagon has six sides, so it can be divided into six triangles (n/2 = 6/2 = 3).
– L: This term represents the length of one side of the polygon. All sides of a regular polygon are of equal length, so you only need to measure one side to find L.
– R: This term represents the radius of the inscribed circle. The radius is the distance from the center of the polygon to the midpoint of one of its sides.
Once you have all the values for n, L, and R, you can plug them into the formula and calculate the area of the regular polygon.
The formula for finding the area of a regular polygon is A = (n/2) * L * R, where n is the number of sides, L is the length of one side, and R is the radius of the inscribed circle.
What is the Apothem of a Circle?
In geometry, the apothem of a circle is defined as the perpendicular distance from the center of a circle to a chord of the same circle. In simpler terms, imagine drawing a straight line from the center of a circle to the midpoint of one of its sides – this line is the apothem of the circle.
The apothem is an important measurement when calculating the area and perimeter of a polygon inscribed within a circle. By drawing an apothem, we can divide the polygon into congruent triangles, making it easier to calculate the area and perimeter.
It is worth noting that the apothem is not the same as the radius of a circle. The radius is the distance from the center to any point on the circumference of the circle, wheres the apothem is the distance from the center to a chord of the same circle.
To calculate the apothem of a circle, one can use the formula:
Apothem = radius × cos(180°/n)
Where “n” is the number of sides of the polygon inscribed within the circle. Alternatively, if the length of one side of the polygon is known, the apothem can be calculated using the formula:
Apothem = 0.5 × side length × cot(180°/n)
The apothem of a circle is the distance from the center to a chord of the same circle. It is an important measurement when calculating the area and perimeter of polygons inscribed within circles.
Is the Apothem Equal to the Side Length?
The apothem is not equal to the side length of a polygon. The apothem is a line segment that connects the center of the polygon to the midpoint of one of its sides. It is perpendicular to that side and is the shortest distance from the center to the side. The side length, on the other hand, is the distance between two consecutive vertices of the polygon.
The apothem is an important measurement in polygons becaue it is used to calculate the area of a polygon using the formula A = (1/2)ap, where A is the area of the polygon, a is the apothem, and p is the perimeter of the polygon.
It’s worth noting that the apothem is also the radius of the inscribed circle of the polygon, which is the largest circle that can be drawn inside the polygon without crossing any of its sides. The inscribed circle touches each side of the polygon at exactly one point.
The apothem and the side length are two different measurements in polygons. The apothem is the shortest distance from the center of the polygon to a side, while the side length is the distance between two consecutive vertices of the polygon.
Conclusion
The apothem of a regular polygon is an important geometric feature that helps us calculate other important properties of the polygon. We can find the length of the apothem by using the formula A = (1/2)ap, whre A is the area of the polygon, a is the length of the apothem, and p is the perimeter of the polygon. Similarly, if we know the area and perimeter of the polygon, we can solve for the apothem using the formula a = 2A / P.
The apothem is an essential element in the construction of regular polygons and is used in various fields, including architecture, engineering, and design. By understanding the concept of apothem and its formula, we can calculate the area, perimeter, and other important properties of a regular polygon with ease.
To conclude, the formula of apothem is a valuable tool for solving problems related to regular polygons, and its understanding is crucial for anyone who wants to explore the fascinating world of geometry.
