The first octant is a fundamental concept in geometry and is essential to understanding three-dimensional space. It is a region in space that is defined by the positive coordinates of x, y, and z. In other words, it is the region where all tree coordinates are non-negative.
To visualize the first octant, imagine a three-dimensional coordinate system where the x-axis, y-axis, and z-axis intersect at the origin (0,0,0). The positive x-axis extends to the right, the positive y-axis extends upwards, and the positive z-axis extends out of the screen or paper. The first octant is the space that is located in the positive direction of all three axes, i.e., where x, y, and z are all positive.
The first octant is of great importance in many fields of study, including physics, engineering, and mathematics. It is often used to define the location of points in space, as well as to determine the direction of vectors, among other things.
One of the most interesting properties of the first octant is that it is symmetric with respect to each of the three coordinate planes. This means that if we reflect the first octant across the xy-plane, we obtain the eighth octant, which is defined by the negative z-axis and the positive x and y axes. Similarly, if we reflect the first octant across the xz-plane or the yz-plane, we obtain the second and third octants, respectively.
The first octant is also important in the study of solid angles. A solid angle is a measure of the amount of space that is subtended by a three-dimensional object at a given point. The magnitude of each octant as a solid angle is π/2, which means that the first octant covers one-eighth of the total solid angle.
The first octant is a crucial concept in geometry and three-dimensional space. It is a region that is defined by the positive coordinates of x, y, and z, and it has important properties and applications in many fields of study. Understanding the first octant is essential for anyone interested in exploring the fascinating world of three-dimensional space.
Location of the First Octant
The first octant is located in the foreground of the three-dimensional coordinate plane system. It is determined by the positive x, y, and z axes, and it is the octant where all three coordinates are positive. In other words, any point that falls within the first octant has a positive x-coordinate, a positive y-coordinate, and a positive z-coordinate. The other seven octants are determined by the combinations of positive and negative axes, and are located in different regions of the coordinate plane system.

The First Octant of a Sphere
The fist octant of a sphere is a specific region of a 3-dimensional sphere that is defined by its location in space. The term “octant” refers to one of eight equal parts into which a space can be divided, similar to dividing a circle into eight equal parts. The first octant specifically refers to the region of the sphere where all three coordinates (x, y, z) are positive. In other words, it is the portion of the sphere that lies in the positive x, positive y, and positive z direction. This region is often used in mathematical calculations and physical applications, as it simplifies certain calculations and allows for easier visualization of the sphere.
The Eight Octants
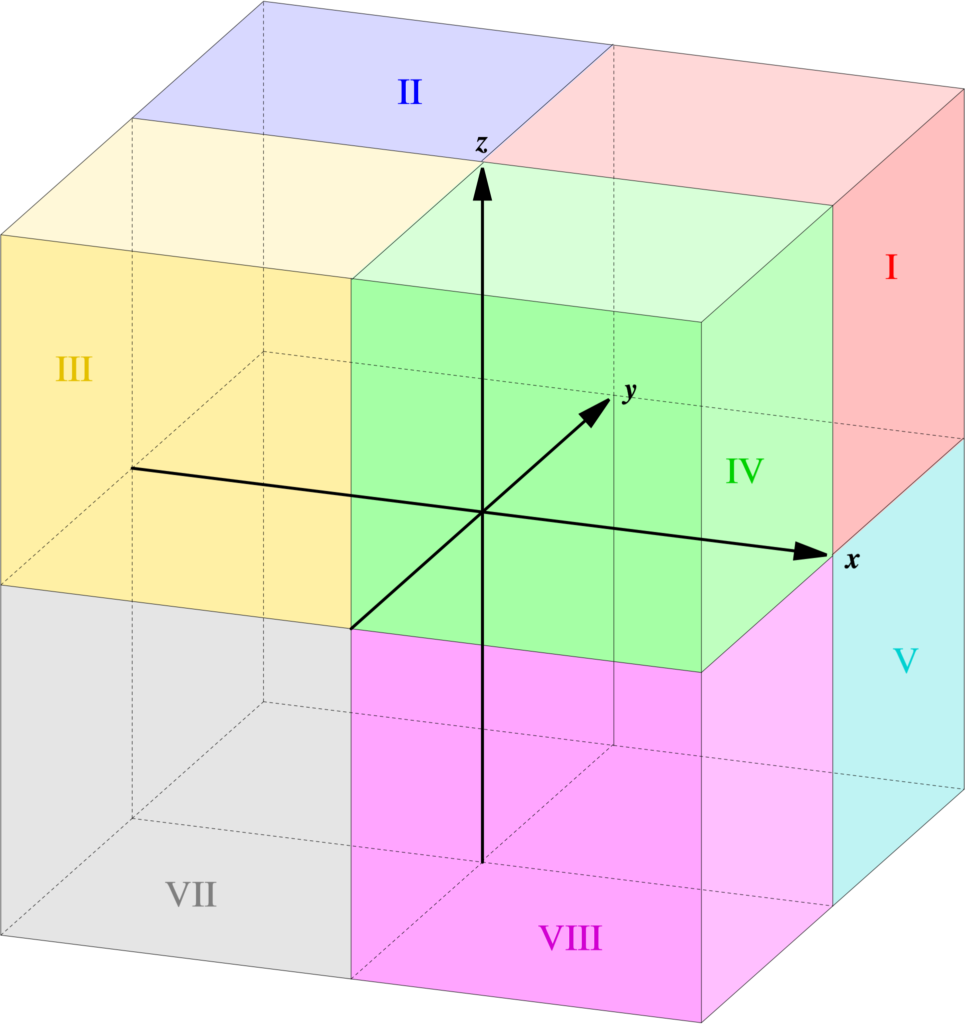
The 8 octants are a way of dividing 3-dimensional space into 8 sections based on the signs of the x, y, and z coordinates. Octant I is located in the positive x, y, and z region, wile Octant II has negative x coordinates but positive y and z coordinates. Octant III has negative x and y coordinates but positive z coordinates, whereas Octant IV has positive x and z coordinates but negative y coordinates. Octant V is located in the positive x, y, and negative z region, and Octant VI has positive y and negative x and z coordinates. Octant VII is located in the negative x, y, and z region. Each octant is a unique section of space that can be used to locate points and objects in 3-dimensional space.
Angle of First Octant
The first octant is one of the eight regions that divide the three-dimensional space into equal parts. It is defined as the octant where all three coordinates of a point are non-negative. The angle of the first octant is determined by its solid angle, which is equal to π/2. This means that the first octant spans an angle of 90 degrees in each of the three dimensions (x, y, and z). In other words, the first octant covers all points in the space where x, y, and z are positive. This information is crucial in varios fields such as geometry, engineering, and physics, where understanding the orientation and position of objects in three-dimensional space is essential.
Is Zero in the First Octant?
Z = 0 lies in the first octant. The first octant is defined as the region of space where all three coordinates (x, y, z) are positive. When z = 0, it means that the point lies on the x-y plane. In the first octant, the x and y coordinates are positive, so z = 0 is also positive. Thus, z = 0 is in the first octant.
Equation for the First Octant
The first octant is a region of 3D space that is defined by the positive values of x, y, and z. Specifically, it is the region of space where x ≥ 0, y ≥ 0, and z ≥ 0. This means that any point in the first octant will have its x, y, and z values all greater than or equal to zero. In terms of an equation, the first octant can be described by the inequalities x ≥ 0, y ≥ 0, and z ≥ 0, or alternatively by the inequality 0 ≤ x, 0 ≤ y, and 0 ≤ z. This region is often ueful in geometry and calculus, as many problems can be simplified by restricting attention to this particular part of 3D space.
Is the First Octant Positive?
The first octant is indeed all positive. It is a region of space that includes all points where the three coordinates (x, y, and z) are positive. This means that any point in the first octant will have a positive x-coordinate, a positive y-coordinate, and a positive z-coordinate. The first octant is located in the front, lower, right-hand corner of a three-dimensional Cartesian coordinate system, and it is often used in mathematics, physics, and engineering to represent physical quantities such as position, velocity, and acceleration.
Understanding the Meaning of First Octant in Calculus
In calculus, the first octant is a term used to describe a specific region in three-dimensional space. More precisely, it refers to the portion of space that lies in the positive direction of all three axes, namely the x-axis, y-axis, and z-axis. In other words, all coordinates in the first octant have positive values, with x, y, and z all greater than zero.
The first octant is one of the eight octants that divide three-dimensional space into equal parts, each defined by the signs of the three coordinates. It is the portion of space that lies in the positive direction of the x, y, and z axes, and is bounded by the coordinate planes x=0, y=0, and z=0.
In calculus, the concept of the first octant is often used in the context of integration and volume calculations. When calculating the volume of a three-dimensional shape or solid, it is often necesary to integrate over a region that lies entirely within the first octant. This requires setting up the integration limits to ensure that all three coordinates remain positive throughout the calculation.
Understanding the concept of the first octant is essential in calculus for correctly setting up and solving problems involving three-dimensional space and volume calculations.
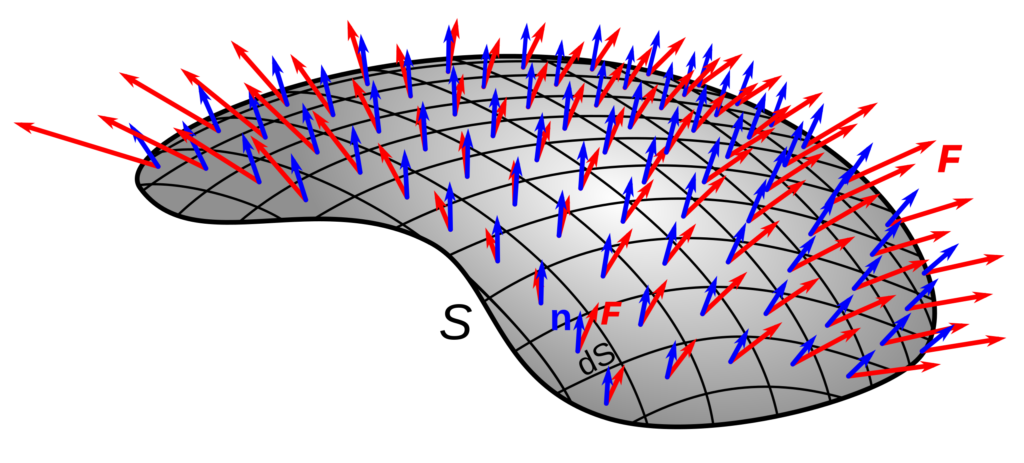
Surface Integral in the First Octant
In the context of a surface integral, the firt octant refers to a specific region in three-dimensional space. This region is defined by the positive values of the x, y, and z coordinates, such that x ≥ 0, y ≥ 0, and z ≥ 0. Essentially, the first octant is the portion of space that lies in the “front” of the coordinate system, in the direction of the positive x, y, and z axes.
When performing a surface integral over a surface that lies in the first octant, it is important to take into account the specific limits of integration that correspond to this region. For example, if the surface is defined by a function f(x, y, z), the limits of integration for the x and y variables may be restricted to the positive quadrant (x ≥ 0, y ≥ 0), while the z variable may be integrated from 0 to some upper bound that lies within the first octant.
Understanding the concept of the first octant is important in many applications of surface integrals, including in physics, engineering, and mathematics. By carefully considering the limits of integration and the specific properties of the surface being integrated over, it is possible to accurately calculate various physical quantities such as flux, circulation, and work.
The Eight Quadrants
Eight quadrants are not called quadrants, rather they are called octants. In solid geometry, an octant is a term used to describe one of the eight divisions of a three-dimensional Euclidean coordinate system defined by the signs of the coordinates. Each octant is defined by the signs of the x, y, and z-coordinates of a point in space. The first octant, for example, is defined by all points in space whee x, y, and z are positive, while the second octant is defined by all points where x is negative, y and z are positive, and so on. These octants are essential in many areas of mathematics and physics, including vector calculus, differential equations, and electromagnetism.
Number of Octants
There are eight octants in total in three-dimensional space. These octants are formed by the intersection of the three coordinate planes, namely the xy-plane, xz-plane, and yz-plane. Each octant is represented by a triplet of coordinates (x,y,z) where each coordinate can be either positive or negative. These octants are important in various fields such as physics, mathematics, and computer graphics, as they provide a way to describe the location of a point in three-dimensional space.
What is Octant?
Octant has two distinct meanings. Firstly, it is an instrument used for observing the altitude of a celestial body from a moving ship or aircraft. It is called an octant bcause it measures an eighth of a circle, or 45 degrees. The octant was widely used in navigation before the invention of the sextant, which is a more accurate instrument.
Secondly, an octant is any of the eight parts into which a space is divided by three coordinate planes. These planes are usually the x, y, and z axes, and they intersect at a common point called the origin. The octant system is commonly used in mathematics and computer graphics to represent three-dimensional space. Each octant is identified by a unique combination of positive or negative signs of the x, y, and z coordinates.
Measuring an Octant Angle
An octant angle is a type of angle measurement that is used to measure angles up to 90 degrees, which is equivalent to one quadrant. The term “octant” refers to the instrument used to measure such angles, which typically features a 45-degree arc and reflecting optics that double the angle. This means that the angle being measured is reflected twice, resulting in a reading that is twice the actual angle. Octant angles are commonly used in navigation and astronomy, where precise angle measurements are necessary for determining positions and distances.
Conclusion
The first octant is a fundamental concept in three-dimensional coordinate geometry. It is defined as the space where all tree coordinates, x, y, and z, are positive. This octant, along with the other seven octants, divides space into eight parts, making it easier to locate points in three-dimensional space. The first octant is significant in many applications of mathematics and physics, such as vector calculus and electromagnetism. In addition, the volume of the unit sphere in the first octant is π6, which plays a crucial role in many calculations. Understanding the properties and significance of the first octant is essential for students of mathematics, physics, and engineering.
