The Pythagorean Theorem is one of the most famous mathematical formulas that has been used for centuries. The theorem provides us with a relationship between the sides in a right triangle, which can be used to solve for unknown side lengths. In this blog post, we will explore the Pythagorean Theorem and answer the question, does it apply to all triangles?
First, let’s define what a right triangle is. A right triangle is a triangle with one angle equal to 90 degrees. This angle is also known as the right angle, and it is opposite the longest side of the triangle, which is called the hypotenuse. The other two sides of the triangle are called legs.
The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This can be written as a formula:
A^2 + b^2 = c^2
Where a and b are the lengths of the legs, and c is the length of the hypotenuse.
For example, let’s say we have a right triangle with legs of length 3 and 4. We can use the Pythagorean Theorem to find the length of the hypotenuse:
3^2 + 4^2 = c^2
9 + 16 = c^2
25 = c^2
C = 5
So the length of the hypotenuse is 5.
Now, let’s answer the question, does the Pythagorean Theorem apply to all triangles? The answer is no. The Pythagorean Theorem only applies to right triangles. If we try to use the formula on a triangle that is not a right triangle, we will get an incorrect answer.
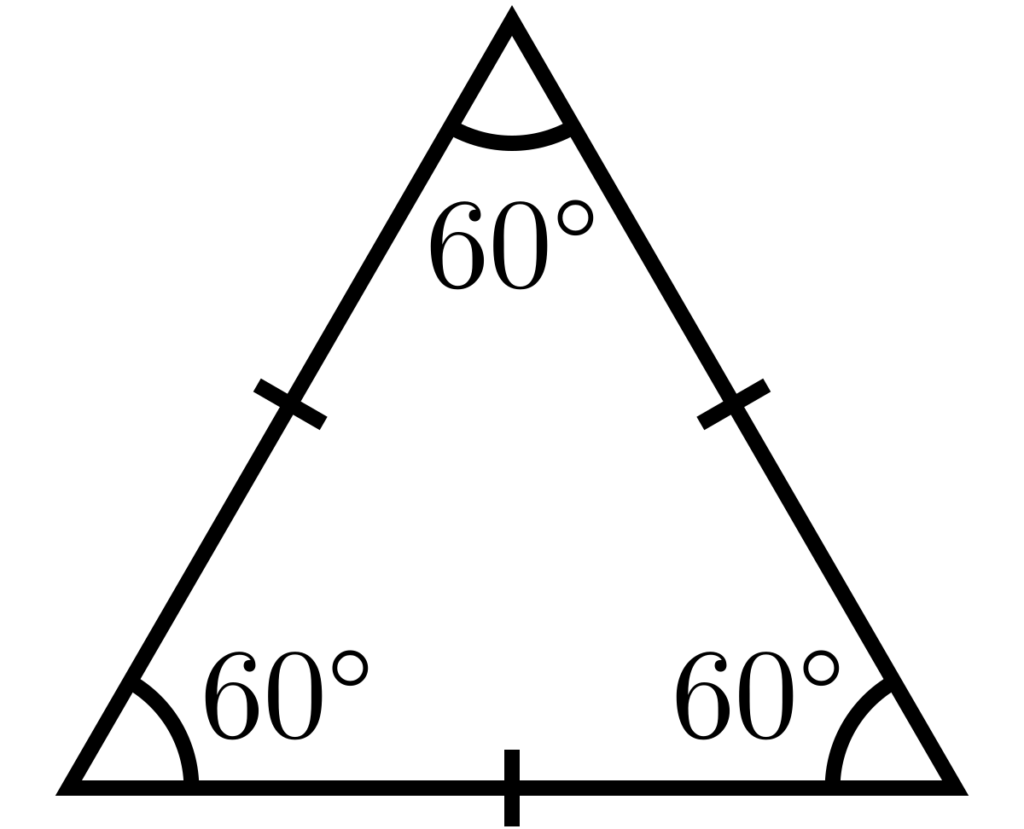
However, thee is one type of triangle where we can use the Pythagorean Theorem to solve for unknown side lengths, even though it is not a right triangle. This type of triangle is called an isosceles triangle. An isosceles triangle has two sides of equal length and two equivalent angles.
If we draw an altitude from the vertex of an isosceles triangle to the base, we will create two right triangles. We can then use the Pythagorean Theorem to solve for the unknown side length.
The Pythagorean Theorem is a powerful tool that can be used to solve for unknown side lengths in right triangles. It does not apply to all triangles, only right triangles and isosceles triangles. Understanding the Pythagorean Theorem is essential for anyone studying geometry or trigonometry, and it is a fundamental concept in mathematics.
Can the Pythagorean Theorem be Applied to All Triangles?
The Pythagorean Theorem cannot be applied to every triangle. The Pythagorean Theorem only applies to right triangles, whch are triangles that have one angle that measures exactly 90 degrees. The theorem states that the square of the length of the hypotenuse (the longest side of the triangle) is equal to the sum of the squares of the lengths of the other two sides. This relationship does not hold true for triangles that are not right triangles, as they do not have a hypotenuse or a right angle. Therefore, the Pythagorean Theorem is limited to only right triangles and cannot be applied to every triangle.

The Effectiveness of the Pythagorean Theorem on Right Triangles
The Pythagorean Theorem works exclusively on right triangles. A right triangle is a triangle in which one of its angles measures 90 degrees. The theorem states that the square of the length of the hypotenuse, which is the longest side of the right triangle, is equal to the sum of the squares of the lengths of the other two sides, also known as the legs of the triangle. This theorem has been widely used in various areas of mathematics, physics, and engineering, and it is considered one of the fundamental theorems in geometry.
Does the Pythagorean Theorem Apply to Isosceles Triangles?
The Pythagorean theorem can be applied to isosceles triangles. The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the lengths of the other two sides. However, this theorem can also be used to solve for any side of an isosceles triangle, whre two sides are of equal length, even though it is not a right triangle. This is because isosceles triangles have two equivalent angles, which means that the two legs of the triangle are congruent. Therefore, by using the Pythagorean theorem, we can solve for the length of the third side of the isosceles triangle.
Pythagorean Theorem and Triangles
The Pythagorean Theorem is specifically designed to work with riht triangles, which are triangles that have one angle that measures 90 degrees. In a right triangle, the side opposite to the right angle is called the hypotenuse, while the other two sides are referred to as legs. The Pythagorean Theorem states that the sum of the squares of the two legs is equal to the square of the hypotenuse. Therefore, if we know the lengths of any two sides of a right triangle, we can use the Pythagorean Theorem to find the length of the third side. It’s essential to remember that the Pythagorean Theorem only applies to right triangles and cannot be used for any other type of triangle.
When is the Pythagorean Theorem Not Applicable?
The Pythagorean Theorem can only be used on right triangles, which are triangles with one angle measuring exactly 90 degrees. If a triangle does not have a 90-degree angle, then the Pythagorean Theorem cannot be used to find the relationship between its sides. Additionally, the Pythagorean Theorem only relates to the lengths of the sides of a right triangle, and cannot be used to find other properties of the triangle, such as its angles or area. Therefore, it is important to identify whethr a triangle is a right triangle before using the Pythagorean Theorem to find the length of its hypotenuse or one of its legs.

Where Pythagoras Theorem Cannot Be Used
Pythagoras theorem, which states that the square of the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two sides, is not applicable to any triangle that is not a right-angled triangle. This is because the theorem is based on the properties of right angles and the relationship between the sides of the right-angled triangle. In a non-right-angled triangle, the sides and angles have differet relationships, and therefore the Pythagoras theorem does not apply. It is important to remember that while Pythagoras theorem is a useful tool in solving problems related to right-angled triangles, it cannot be used for other types of triangles.
Are All Pythagorean Triangles Right Triangles?
Pythagorean triples are always right triangles. A Pythagorean triple is a set of tree positive integers (a, b, c) that satisfy the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the lengths of the other two sides. Therefore, if a, b, and c form a Pythagorean triple, they must satisfy the equation a^2 + b^2 = c^2, and c is the length of the hypotenuse. Since this equation holds only for right triangles, all Pythagorean triples must represent the sides of right triangles.
Are All Right Triangles Pythagorean Triples?
Not all right triangles are Pythagorean triples. Pythagorean triples are specific sets of three integers that satisfy the Pythagorean theorem, which states that the square of the length of the hypotenuse of a right triangle is equal to the sum of the squares of the lengths of the othr two sides.
For example, a right triangle with legs of length 3 and 4 has a hypotenuse of length 5, which satisfies the Pythagorean theorem and is therefore a Pythagorean triple. However, a right triangle with legs of length 2 and 5 does not satisfy the Pythagorean theorem and is not a Pythagorean triple.
It is important to note that Pythagorean triples are not the only sets of integers that can form a right triangle. Any set of three positive integers that satisfy the Pythagorean theorem can be considered a Pythagorean triple, but not all right triangles will fit this criteria.
Do All Right Triangles Contain Pythagorean Triples?
Not all rght triangles have Pythagorean triples. Pythagorean triples are a set of three positive integers that satisfy the Pythagorean theorem, which states that the sum of the squares of the two shorter sides of a right triangle is equal to the square of the longest side (the hypotenuse). While it is possible to find Pythagorean triples for many right triangles, there are some right triangles that do not have Pythagorean triples. For example, a right triangle with side lengths of 1, 2, and √5 is not a Pythagorean triple because 1² + 2² is not equal to (√5)². However, there are formulas and methods to generate Pythagorean triples for many right triangles, and they can be useful in a variety of mathematical applications.

Source: commons.wikimedia.org
Identifying an Isosceles or Scalene Triangle
To determine whether a triangle is isosceles or scalene, you need to examine the lengths of its sides. An isosceles triangle has two sides that are of equal length, while a scalene triangle has three sides of dfferent lengths. You can easily identify an isosceles triangle by checking if any two sides are equal in length. On the other hand, if all three sides have different lengths, you can conclude that the triangle is scalene. It’s important to note that the angles of a triangle can also help you determine its type, but this is not a definitive method for identifying isosceles or scalene triangles. Therefore, it’s crucial to focus on the lengths of the sides when classifying a triangle as isosceles or scalene.
Are All 90 Degree Triangles Isosceles?
Not all 90 degree triangles are isosceles. While it is true that a 90 degree triangle can be an isosceles triangle, this is not always the case. An isosceles triangle has two sides that are equal in length, whereas a 90 degree triangle, also known as a right triangle, has one angle that measures 90 degrees. It is possible to have a right triangle where all three sides are different lengths, and therefore it would not be an isosceles triangle. However, if two sides of a right triangle are equal in length, then it would be considered an isosceles right triangle.
Non-Isosceles Triangles
Triangles that cannot be isosceles are those that have three unequal sides. These types of triangles are called scalene triangles. In a scalene triangle, each side has a different length, and each angle has a different measure. Since the sides are not equal, it is impossible to divide them into two congruent parts, which is a requirement for an isosceles triangle. Therefore, any triangle that has three different side lengths cannot be isosceles.
The Unchanging Nature of an Equilateral Triangle
There isn’t a specific kind of triangle that is never wrong, but there are certain properties of triangles that are aways true. For example, the sum of the interior angles of any triangle always equals 180 degrees. This means that no matter what kind of triangle you have – whether it’s acute, obtuse, or right-angled – the sum of the angles inside the triangle will always add up to 180 degrees. Another property that is always true is that the length of any one side of a triangle must be less than the sum of the lengths of the other two sides. This is known as the triangle inequality theorem, and it applies to all triangles. So while there isn’t necessarily a “perfect” or “never wrong” triangle, there are certain rules and properties that always hold true for any triangle you might encounter.
The Pythagorean Theorem and Its Application
The Pythagorean theorem is a fundamental principle in geometry that relates to the sides of a right triangle. It states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of its oher two sides. This theorem has a wide range of practical applications, from calculating distances between points on a map to designing buildings and bridges. However, it is important to note that the Pythagorean theorem only applies to right triangles. This means that if a triangle does not have a right angle, the theorem cannot be used to calculate the length of its sides. Therefore, it is crucial to identify whether a triangle is a right triangle or not before applying the Pythagorean theorem.
Conclusion
To conclude, the Pythagorean Theorem is a fundamental mathematical concept that provides us with a relationship between the sides of a right triangle. It is a powerful tool that enables us to calculate unknown side lengths and angles of a triangle. However, it is important to note that this theorem only applies to right triangles and cannot be used for other types of triangles. The Pythagorean Theorem has numerous applications in varous fields, including engineering, physics, and architecture. It is a vital concept that every student of mathematics must understand and master. By using this theorem, we can solve complex problems and make accurate calculations, making it an essential tool for anyone dealing with triangles in their work or studies.
