Reflection is an essential concept in geometry that involves the transformation of a geometric figure across a line or a plane. This transformation results in a mirror image of the original figure, and it is an isometric transformation, meaning that the size and shape of the figure remain the same. However, the orientation of the vertices may change in a reflection.
To understand how the orientation of the vertices changes in a reflection, we must first know what vertices are. Vertices are the points where the edges of a geometric figure meet. In other words, they are the corners of a shape. For example, a square has four vertices, while a triangle has three.
When we apply a reflection to a geometric figure, the figure is flipped across a line or a plane, resulting in a mirror image of the original. The line or plane across whih the figure is reflected is called the line of reflection. The orientation of the vertices changes in a reflection because the figure is flipped, which means that the order in which the vertices were labeled is reversed.
For example, let us consider a square with vertices labeled in a counterclockwise direction as A, B, C, and D. If we reflect this square across a vertical line, the new vertices will be labeled in a clockwise direction as D, C, B, and A. Thus, the orientation of the vertices has changed.
It is important to note that the size and shape of the figure remain the same in a reflection, but the orientation of the vertices changes. This is because the reflection is an isometric transformation that preserves the distance between the vertices and the angles between the sides of the figure.
Reflection is an essential concept in geometry that involves the transformation of a geometric figure across a line or a plane. The orientation of the vertices changes in a reflection because the order in which they were labeled is reversed. However, the size and shape of the figure remain the same, making it an isometric transformation.
Effects of Changing the Orientation of Vertices
The orientation of a geometric figure’s vertices is determined by the order in which they are labeled. If the vertices are labeled in a clockwise order, for example, the figure is said to have a clockwise orientation. Conversely, if the vertices are labeled in a counterclockwise order, the figure has a counterclockwise orientation.
The orientation of the vertices can be changed by altering the order in which they are labeled. This can be done manually by re-labeling the vertices in a different order, or through certain transformations such as reflections or shears. These transformations can cause the order of the vertices to be reversed, which in turn changes the orientation of the figure.
It is important to note that while the orientation of a figure’s vertices can change, certain properties of the figure remain the same. For example, the area of a figure is independent of its orientation, so a figure with a clockwise orientation will have the same area as a figure with a counterclockwise orientation, as long as the vertices are in the same locations relative to each other.
Source: mdpi.com
Does Translation Affect the Orientation of Vertices?
The orientation of the vertices does not change in translation. Translation only involves moving the entire figure in a specific direction without rotating or flipping it. This means that the vertices of the figure will maintain the same relative position to each other and the angles between them will remain the same. The only change is in the location of the figure on the coordinate plane.
Effect of Dilation on Vertex Orientation
The orientation of the vertices does not change in a dilation. A dilation is a transformation that changes the size of a figure, but it does not affect the shape or orientation of the figure. The vertices of the original figure are simply scaled up or down by the same factor as the rest of the figure, preserving their relative position and orientation. Therefore, the orientation of the vertices remains the same in a dilation.
Why Reflections Do Not Preserve Orientation
Reflection transformations involve flipping an object over a fixed line, which causes a change in the object’s angle positions relative to the x and y axis on a graph. This change in angle positions results in a reversal of orientation, which means that the object’s left and right sides are swapped. For example, if you reflect the letter “F” over a vertical line, it becomes a mirror image of itself, and the left and right sides are reversed. This is why reflections do not preserve orientation. In contrast, transformations such as translations, rotations, and dilations do preserve orientation bcause they do not involve flipping or reversing the object.
Orientation of Reflection
The orientation of reflection refers to the arrangement or positioning of points, lines or shapes relative to each other after a reflection transformation has occurred. Specifically, it refers to the direction in which the reflection occurred. A reflection can occur horizontally, vertically or diagonally, and the orientation will differ depending on the direction of the reflection. For example, if a shape is reflected horizontally, the orientation will be reversed left to right, while if it is reflected vertically, the orientation will be reversed top to bottom. Similarly, if a shape is reflected diagonally, the orientation will be reversed at an angle, depending on the direction of the reflection. Thus, understanding the orientation of reflection is crucial in accurately describing and analyzing the changes that occur in a shape or figure after a reflection transformation has tken place.

Effects of Reflection on a Figure
After a reflection, a figure undergoes a transformation. The position of the figure changes and it appears as if it has been flipped over a line of reflection. Specifically, the x-coordinate of each point in the figure remains the same, while the y-coordinate of each point is transformed into its opposite. This means that the figure appears as a mirror image of its original form. To visualize this transformation, one can fold the paper along the line of reflection to see whre the new figure will be located. a reflection changes the orientation and position of a figure with respect to the line of reflection.
Can Reflection Alter Shape?
A reflection transformation cannot change the shape of a figure. When a figure is reflected across a given line, every point on the original figure is mapped to a corresponding point on the reflected figure, maintaining the same distance between them. The reflection only changes the orientation of the figure, but not its shape or size. Therefore, the reflection transformation is a type of rigid transformation, which preserves the geometrical properties of the figure such as congruence, angles, and distances between points.
Factors Influencing Orientation
The orientation factor, κ2, is a crucial parameter that dictates the efficiency of Förster resonance energy transfer. It is determined by the relative orientation of the transition dipole moments of the donor and acceptor species. The transition dipole moment is a measure of the strength and directionality of the absorption and emission of light by a molecule.
In order for energy transfer to occur beween a donor and acceptor molecule, their transition dipoles must be aligned in a specific manner. The κ2 factor accounts for the geometric constraints that affect this alignment. It takes into consideration the relative orientation of the transition dipole moments, as well as the distance and orientation of the molecules in space.
The orientation factor can be influenced by a variety of factors, such as the shape and size of the molecules, as well as any intervening solvent or matrix. In general, κ2 values are higher for donor-acceptor pairs that have a favorable geometry and are positioned close to each other.
The orientation factor κ2 is determined by the orientation of the transition dipole moments of the donor and acceptor molecules, and is influenced by various factors such as their shape, size, and relative distance in space. Understanding and controlling this parameter is crucial for optimizing Förster resonance energy transfer for various applications in fields such as biophysics, materials science, and photonics.
Do Translations Preserve Orientation?
Translations are transformations in which an object is moved in a straight line in a particular direction without any rotation or change in shape. When an object is translated, its orientation is not affected, meaning that the object’s pieces remain in the same order. Therefore, translations aways preserve orientation. In other words, if an object is translated, its left side remains on the left side, and its right side remains on the right side. Similarly, its top remains at the top, and its bottom remains at the bottom. This is because translation only changes the position of the object, and not its orientation. Thus, translations are orientation-preserving transformations.
Source: link.springer.com
Identifying Reflection, Rotation, and Translation
To tell the difference between a reflection, rotation, and translation, it is important to understand their unique characteristics. A reflection is a transformation that flips an object across a line of symmetry. This means that the shape and size of the object remain the same, but it appears as a mirror image of itself. In contrast, a rotation is a transformation that turns an object around a fixed point by a certain degree. This means that the shape and size of the object remain the same, but its orientation changes. Finally, a translation is a transformation that moves an object in a particular direction. This means that the shape, size, and orientation of the object remain the same, but its position changes.
One way to identify which transformation is being used is to look for points or lines that remain fixed during the transformation. For example, during a reflection, any point on the line of reflection will remain fixed. During a rotation, any point on the fixed point (also knwn as the center of rotation) will remain fixed. During a translation, there are no fixed points, but the distance and direction of movement will remain consistent throughout the transformation.
In summary, to identify the type of transformation being used, one should look for changes in orientation, position, and fixed points. Reflections involve a flip across a line of symmetry, rotations involve a turn around a fixed point, and translations involve a slide in a particular direction.
Changing the Orientation of a Figure Through Transformations
There are three types of transformations that can change the orientation of a figure. The first one is translation, which moves the figure in any direction wthout changing its orientation. The second one is reflection, which flips the figure over a line of reflection, changing its orientation to the opposite direction. The third one is rotation, which turns the figure a certain degree around a point, changing its orientation in a circular motion. It is important to note that all three transformations can be used to change the position and orientation of a figure on a plane. However, only reflection and rotation can change the orientation of the figure.
Does Dilation Affect Shape Orientation?
A dilation does not change the orientation of a shape. The process of dilation involves stretching or shrinking an image on the coordinate plane based on a scale factor, but it does not alter the orientation or shape of the original figure. The dilation simply changes the size of the figure while maintaining its original proportions and angles. Therefore, the orientation or direction of the shape remains the same before and after dilation.
The Effects of Dilation on Coordinates
Dilation is a transformation that chanes the size of an object in the coordinate plane. When we dilate an object, we multiply each coordinate of the object by a scale factor. The scale factor is a number that determines how much the object will be scaled. The center of dilation is usually the origin, unless otherwise specified.
To understand how dilation changes the coordinates, let’s take an example. Suppose we have a point with coordinates (2,3) and we want to dilate it with a scale factor of 2. The mapping for the dilation will be (x,y) → (2x, 2y). So, when we apply this mapping to the point (2,3), we get:
(2,3) → (2(2), 2(3)) = (4,6)
As you can see, the coordinates of the point have been multiplied by the scale factor of 2 to get the new coordinates of (4,6). Therefore, the dilation has changed the size of the point, making it twice as big as the original point.
Dilation changes the coordinates of an object by multiplying each coordinate by a scale factor. This transformation changes the size of the object and the center of dilation is usually the origin.
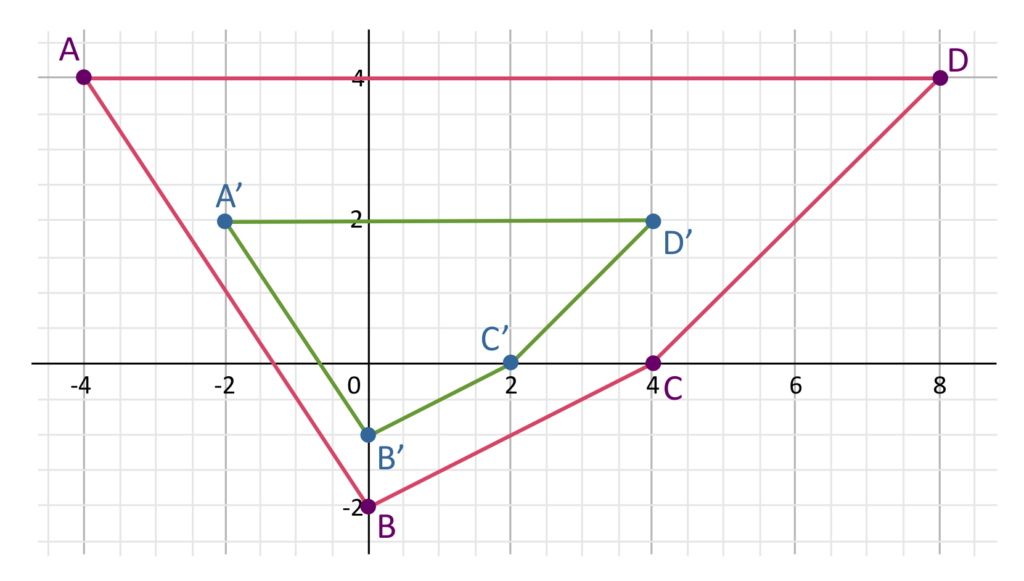
The Effects of Dilations on Coordinates
Dilations are transformations that change the size of a figure whle maintaining its shape. When a dilation is performed on a figure, all of its coordinates are affected. Specifically, the coordinates of the new figure are found by multiplying the coordinates of the original figure by a scale factor. The scale factor is the ratio of the side lengths of the new figure to the side lengths of the original figure. If the scale factor is greater than 1, the figure is enlarged. If the scale factor is less than 1, the figure is shrunk. Moreover, if the scale factor is negative, the figure is reflected across the origin. In general, dilations affect the coordinates of a figure by stretching or shrinking them in relation to a fixed point, called the center of dilation.
Conclusion
Reflections are a type of transformation that involves flipping a geometric figure over a line of reflection. They are isometric, meaning they preserve the size and shape of the figure, but they do not preserve orientation. The orientation of a figure is determined by the order in which its vertices are labeled, which can be either clockwise or counterclockwise. The order of the vertices is preserved during translations, dilations, and rotations, which are other types of transformations that can be applied to geometric figures. Reflections are important in geometry beause they can be used to solve problems and prove theorems, and they have practical applications in fields such as engineering, architecture, and computer graphics. reflections are a fundamental concept in geometry that can help us to better understand the properties and behavior of geometric figures.
