Triangles are one of the most basic and important shapes in geometry. They have been studied for centuries and thir properties are essential in many fields of mathematics and science. One of the most useful tools for working with triangles is trigonometry, which involves the study of the relationships between angles and sides in triangles.
One of the most commonly used methods in trigonometry is SOHCAHTOA, which stands for Sine, Cosine, and Tangent. This method is used to find the missing sides or angles of right triangles, where one of the angles measures 90 degrees. But what about non-right triangles? Does SOHCAHTOA work on all triangles?
The short answer is no, SOHCAHTOA does not work on all triangles. SOHCAHTOA is only applicable to right triangles, where one of the angles is 90 degrees. This is because the ratios of the sides of a right triangle are fixed and can be used to determine the missing side lengths or angles.
However, there are other methods of trigonometry that can be used to solve non-right triangles. The most commonly used method is the Sine Rule, which states that the ratio of the length of a side to the sine of its opposite angle is the same for all sides in a triangle. This means that if you know two sides and the angle opposite one of them, you can use the Sine Rule to find the missing side or angle.
Another method that can be used for non-right triangles is the Cosine Rule, which relates the lengths of the sides to the cosine of one of the angles. This rule can be used to find any side or angle in a triangle if the other two sides and the included angle are known.
It is important to note that while SOHCAHTOA is limited to right triangles, the principles of trigonometry can be applied to all triangles. Any non-right triangle can be divided by an altitude into two right triangles, which can then be solved using SOHCAHTOA or other trigonometric methods.
While SOHCAHTOA is a useful tool for solving right triangles, it is not applicable to all triangles. The Sine Rule and Cosine Rule are two other important methods of trigonometry that can be used to solve non-right triangles. By understanding these principles, we can gain a deeper understanding of the relationships between angles and sides in all types of triangles.
The Use of Sin, Cos, and Tan on Triangles
You cannot use Sin Cos Tan on any triangle. Sin Cos Tan are trigonometric ratios used for right-angled triangles only. However, you can use the Sine Rule and Cosine Rule to solve triangles that are not right-angled. The Sine Rule is used when you have a side and its opposite angle, while the Cosine Rule is used when you have two sides and the included angle. It’s important to use the correct formula for the given situation to get accurate results.
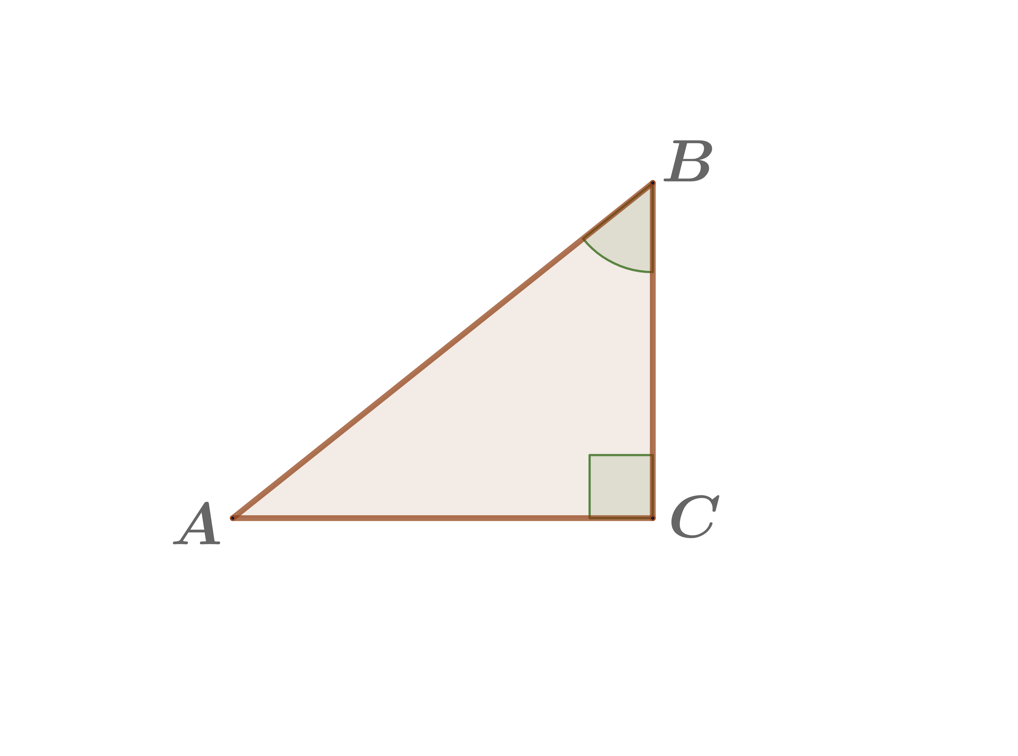
Using Trigonometry on Non-Right Triangles
Trigonometry can be applied to non-right triangles by dividing them into two right triangles using an altitude. This is because any non-right triangle can be split into two right triangles, and the trigonometric functions can be used to solve for the unknown sides and angles in each of the right triangles. This technique is called the Law of Sines and Law of Cosines, which are formulas used to find the missing sides and angles of a non-right triangle. Therefore, trigonometry can be used to solve problems involving non-right triangles as well.
Does the Sin and Cos Function Work for All Triangles?
Sin and cos do not work for all triangles. They only work for right triangles, whch are triangles that have one angle measuring 90 degrees. In a right triangle, the sine of an angle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse (the longest side of the triangle). Similarly, the cosine of an angle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. However, for non-right triangles (such as acute or obtuse triangles), you need to use the Law of Sines or the Law of Cosines to find the missing sides and angles.
The Effectiveness of Trigonometry in All Triangles
Trigonometry can be used for all types of triangles, not just riht triangles. The principles of trigonometry, such as the sine, cosine, and tangent ratios, can be applied to any triangle to calculate the lengths of its sides and measure its angles. In fact, trigonometry is one of the most useful tools for solving problems involving triangles, as it allows us to determine the unknown measurements of a triangle based on the known measurements of other sides and angles. Additionally, trigonometry can also be used to solve problems involving complex shapes that can be broken down into smaller triangles. Therefore, whether it is a right triangle, acute triangle, or obtuse triangle, trigonometry can be used to find the missing measurements and solve problems involving the triangle.
When is Sohcahtoa Not Applicable?
Sohcahtoa is a mnemonic device that helps us remember the trigonometric ratios of sine, cosine, and tangent in relation to the angle and sides of a right triangle. However, it is important to note that Sohcahtoa only applies to right triangles. If we have an oblique triangle, whee none of the angles are 90 degrees, then we can’t assume these trig ratios will work. In oblique triangles, we have to use other trigonometric functions such as the Law of Sines and Law of Cosines to solve for the unknown sides and angles. Therefore, we can conclude that Sohcahtoa is limited to right triangles and cannot be used for oblique triangles.

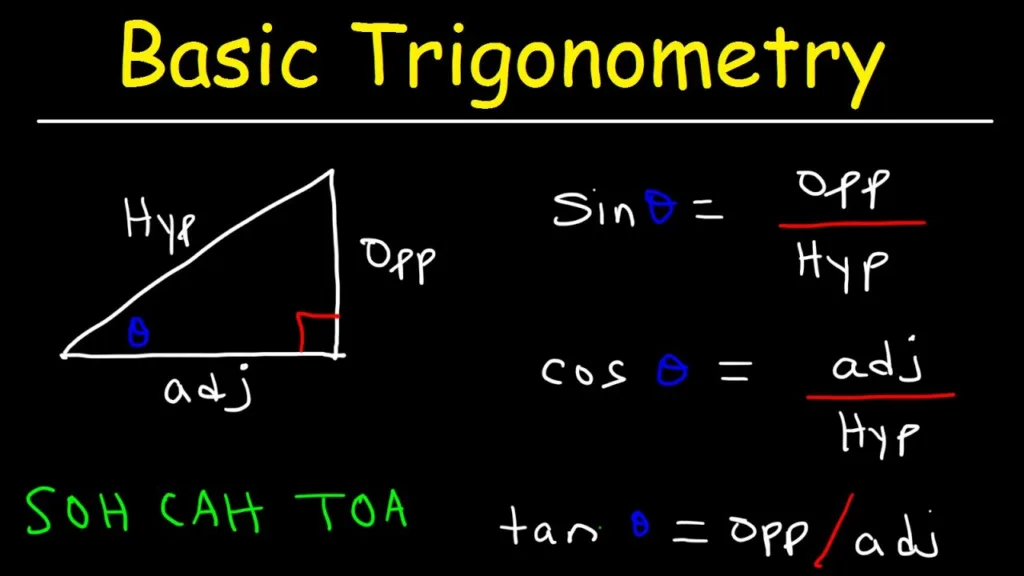
When to Use Sin, Cos, and Tan
To determine whether to use sine, cosine, or tangent in a right triangle, you need to identify which two sides of the triangle are given. If you know the length of the opposite side and the length of the hypotenuse, you can use sine. If you know the length of the adjacent side and the length of the hypotenuse, you can use cosine. And, if you know the length of the opposite and adjacent sides, you can use tangent. This can be easily remembered by using the acronym SOH CAH TOA, whee S stands for sine, O stands for opposite, H stands for hypotenuse, C stands for cosine, A stands for adjacent, and T stands for tangent.
Using SOH CAH TOA on Non-Right Angles
SOHCAHTOA is a mnemonic device used to remember the trigonometric ratios for right-angled triangles. The three ratios are sine (sin), cosine (cos), and tangent (tan). These ratios relate the sides of a right-angled triangle to its angles. However, they are only applicable to right-angled triangles.
Non-right angled triangles require a different approach to solve for their unknown sides and angles. One method is to use the Law of Sines or the Law of Cosines. The Law of Sines relates the sides of a triangle to the sines of their opposite angles, wile the Law of Cosines relates the sides and angles of a triangle to each other. These laws can be used to solve for unknown sides and angles in non-right angled triangles.
SOHCAHTOA is not applicable to non-right angled triangles, and different methods such as the Law of Sines or the Law of Cosines should be used instead.
Can Sohcahtoa Be Used on a 90 Degree Angle?
You cannot use Sohcahtoa on a 90 degree angle. Sohcahtoa is a mnemonic that refers to the three trigonometric ratios: sine, cosine, and tangent. These ratios are used to find the relationship between the sides and angles of a right triangle. However, when the angle of a triangle is 90 degrees, it is no longer a right triangle and the sides are not related by the trigonometric ratios. In this case, you would need to use different methods such as the Pythagorean theorem to find the relationship between the sides.
Does Pythagoras’ Theorem Apply to All Triangles?
Pythagoras’ theorem only applies to right-angled triangles, which are triangles with one angle measuring 90 degrees. This theorem states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Therefore, if a triangle is not right-angled, Pythagoras’ theorem canot be used to find the length of its sides or determine its angles. In such cases, other mathematical formulas and principles, such as the Law of Sines and the Law of Cosines, are used to solve for the unknown values in the triangle.
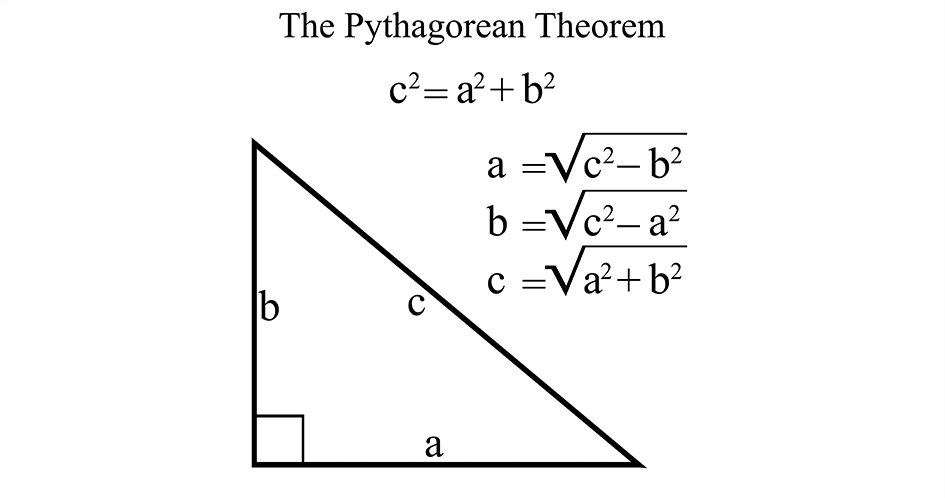
Solving Problems That Cannot Be Solved Using the Law of Sines
The Law of Sines is a trigonometric method used to solve for the missing sides or angles of a triangle. However, there are certain cases where the Law of Sines cannot be used to find a solution. For instance, if we are given two sides and an included angle of a triangle or if we are given three sides of a triangle, we cannot use the Law of Sines because we cannot set up any proportions where enouh information is known. In other words, we do not have sufficient information to use the Law of Sines to solve for the missing sides or angles. In such cases, we may need to use other trigonometric methods, such as the Law of Cosines, to find a solution.
Can Cosine Only Be Used on Right Triangles?
The cosine function (cos) can be used on any type of triangle, not just right triangles. The cosine of an angle in a triangle is defined as the ratio of the adjacent side to the hypotenuse, where the adjacent side is the side adjacent to the angle and the hypotenuse is the longest side of the triangle. This means that the cosine function can be used to find the length of any side of a triangle, given the lengths of the other two sides and the angle between them. Therefore, the cosine function can be used to solve problems involving any type of triangle, whethr it is acute, right, or obtuse.
Triangles That Cannot Be Solved
Triangles that cannot be solved are those that do not have enough information to determine the length of their sides or the measure of their angles. Specifically, triangles that have only three angles givn (AAA) cannot be solved because there are infinitely many triangles that have the same three angles. In order to solve a triangle, we need to know at least one side and one angle (AAS or ASA), two sides and an included angle (SAS), or all three sides (SSS). These conditions provide enough information to use trigonometric functions, such as sine, cosine, and tangent, to find the missing side lengths or angle measures. Therefore, without sufficient information, it is impossible to determine the size and shape of a triangle.
The Difficulty of Trigonometry Compared to Other Mathematical Concepts
Calculus is considered to be harder than trigonometry because it builds upon the concepts learned in trigonometry and introduces new and complex concepts. Calculus deals with the study of change and rates of change, and it involves functions, limits, derivatives, integrals, and differential equations. These concepts require a deep understanding of algebra, geometry, and trigonometry, and they are often used in advanced fields such as physics, engineering, and economics. Therefore, while trigonometry is an important subject, calculus is generally considered to be more difficult due to its advanced nature and the depth of knowledge required to master it.
The Difficulty of Trigonometry
Trigonometry is a branch of mathematics that deals with the study of triangles and teir properties, including the relationships between their angles and sides. It is considered by many to be a challenging and abstract field, requiring a strong foundation in algebra and geometry. Trigonometric concepts such as sine, cosine, and tangent can be difficult to understand and apply, and the use of trigonometric functions and formulas can be complex and require a significant amount of practice to master. However, with dedication and effort, anyone can develop a solid understanding of trigonometry and become proficient in its use. The key to success in trigonometry is to start with a strong foundation in the basics, practice regularly, and seek help when needed.
Conclusion
Triangles are fundamental shapes that exist in our everyday lives. They are used in various fields, including mathematics, engineering, architecture, and art. The study of triangles and their properties has led to the development of trigonometry, which is a branch of mathematics that deals with the relationships beween the sides and angles of triangles. The Pythagorean Theorem is one of the most significant discoveries in the study of triangles, and it has numerous practical applications. We also have the Sine Rule and Cosine Rule that can be used to solve non-right triangles. Understanding triangles and their properties is essential in various fields, and it is an essential concept for anyone studying mathematics. triangles play a crucial role in our daily lives, and they are important for solving real-world problems.
