The rectangle is a fundamental shape in geometry, commonly found in everyday life, and it has numerous properties that make it an interesting and useful shape to study. One of the questions that often comes up when discussing the rectangle is whether it has rotational symmetry. In this post, we will explore the answer to this question and delve deeper into the properties of the rectangle.
Firstly, let’s understand what rotational symmetry is. Rotational symmetry is the property of a shape that allows it to be rotated by a certain angle and still appear the same. In other words, if a shape has rotational symmetry, it will look identical aftr being rotated by a certain angle. The angle of rotation that produces the identical image is known as the order of rotational symmetry.
Now, coming back to the rectangle. Does a rectangle have rotational symmetry? The answer is yes, a rectangle has rotational symmetry of order two. This means that a rectangle looks the same if it is rotated at 180 degrees (half a circle) and 360 degrees (a full circle). You can easily verify this by drawing a rectangle and rotating it by 180 degrees. You’ll see that the resulting image is identical to the original one.
It’s important to note that not all shapes have rotational symmetry. Only certain shapes, like circles, squares, and regular polygons, have rotational symmetry. This is because these shapes have an equal number of sides and angles, which allows them to look the same after being rotated by certain angles.
Apart from rotational symmetry, a rectangle also has reflectional symmetry. This means that a rectangle looks the same when reflected over the line through the midpoints of its opposite sides. You can visualize this by drawing a rectangle and reflecting it over a line passing through the midpoints of its opposite sides. The resulting image will be identical to the original one.
The rectangle is a shape that has both rotational and reflectional symmetry. Its rotational symmetry is of order two, and it can be rotated by 180 degrees and 360 degrees to produce identical images. Rotational symmetry is an important property of shapes, and understanding it can help us better understand the properties of different shapes.
Do Rectangles Possess Rotational Symmetry?
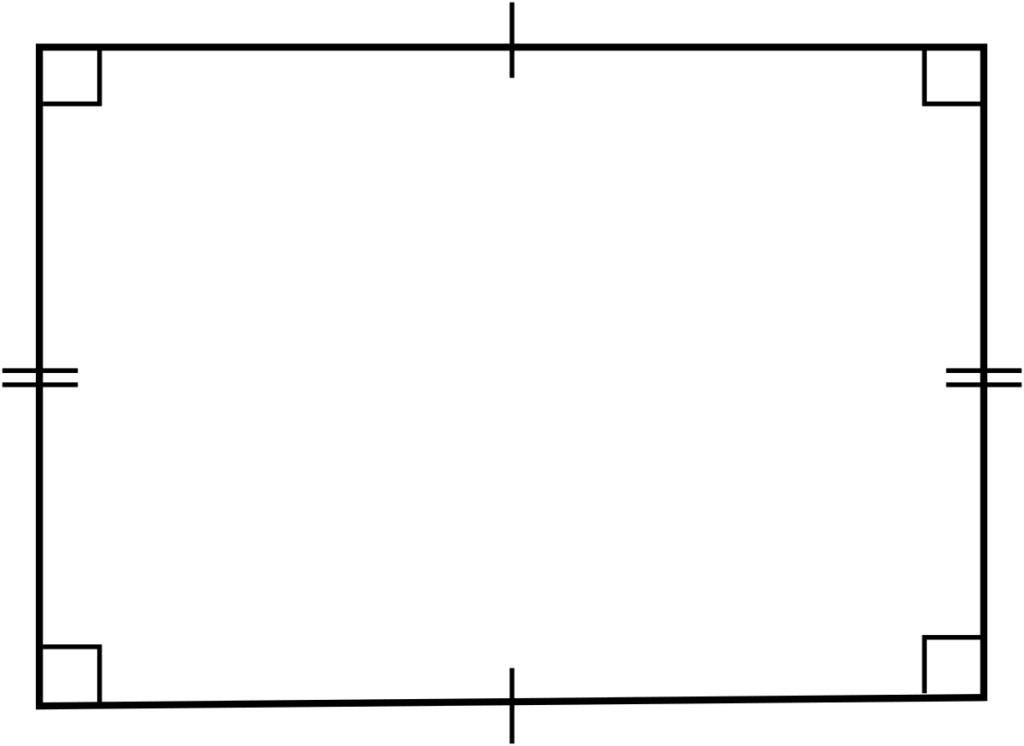
Rectangles have rotational symmetry. A rectangle is a polygon with four sides and four right angles. It has rotational symmetry of order two, which means that it can be rotated 180 degrees and still look the same. This is becase the opposite sides of a rectangle are parallel and of equal length, and the opposite angles are also equal. Therefore, when a rectangle is rotated 180 degrees, the sides and angles remain the same, and the shape still looks identical. Additionally, a rectangle also has two lines of symmetry, which means that it can be divided into two equal halves that are mirror images of each other.
Source: nagwa.com
Does a Rectangle Have 90 Degree Rotational Symmetry?
A rectangle does not have 90 degree rotational symmetry. Rotational symmetry is defined as the ability of a figure to be rotated by a certain angle and still look the same. A rectangle has rotational symmetry of order 2, which means that it can be rotated by 180 degrees and still look the same. However, a rotation of 90 degrees would change the orientation of the rectangle, making it look different. Therefore, a rectangle does not have 90 degree rotational symmetry.
Does a Rectangle Have Symmetry?
A rectangle has both rotational and reflectional symmetry.
The rectangle has rotational symmetry of 180 degrees at its center, which means that if you rotate the rectangle by 180 degrees around its center, it will look the same as it did bfore the rotation. This is because the opposite sides of the rectangle are parallel and equal in length, making it symmetrical when rotated by 180 degrees.
Furthermore, a rectangle has reflectional symmetry when reflected over the line through the midpoints of its opposite sides. This means that if you draw a line through the midpoint of one pair of opposite sides of the rectangle and reflect the rectangle over that line, it will look the same as it did before the reflection. This is because the opposite sides of the rectangle are parallel and equal in length, making it symmetrical when reflected over the line through the midpoints of its opposite sides.
A rectangle has both rotational and reflectional symmetry, making it a symmetrical shape.
Shape with Rotational Symmetry
There are several geometric shapes that exhibit rotational symmetry. These shapes have an axis of rotation, which is a line that passes through the center of the shape and divides it into two equal parts. The shape can be rotated along this axis by a certan angle, and it will appear unchanged or identical to its original position. Some examples of shapes that have rotational symmetry include squares, rectangles, equilateral triangles, regular hexagons, circles, and many more. In general, any shape that is symmetrical around its center point will exhibit rotational symmetry. This property is particularly useful in geometry and design, as it allows for the creation of aesthetically pleasing and mathematically precise patterns and structures.
Lack of Rotational Symmetry
A rotational symmetry is a type of symmetry in which a shape or an object can be rotated by certain degrees without changing its appearance. However, not all shapes or objects possess rotational symmetry. An arrow, for instance, does not have any rotational symmetry because it cannot be rotated by any degree without changing its appearance. If you rotate an arrow, it will look diffeent from its original form, and therefore, it does not have any rotational symmetry. Similarly, a right-angled triangle with different side lengths also does not have any rotational symmetry because it cannot be rotated by any degree without changing its appearance. not all shapes or objects possess rotational symmetry, and an arrow and a right-angled triangle with different side lengths are some examples of shapes that do not have any rotational symmetry.

Does a Rectangle Have 180 Degree Rotation Symmetry?
Rectangles do have 180 degree rotation symmetry. This means that if a rectangle is rotated by 180 degrees about its center point, it will appear exactly the same as it did befre the rotation. In addition to this, rectangles also have two lines of reflective symmetry, which means that they can be reflected over a line of symmetry and still appear the same. These lines of reflective symmetry are the vertical and horizontal lines that pass through the center of the rectangle. a rectangle has a total of four symmetries: 180 degree rotation, as well as reflection over the vertical, horizontal, and diagonal lines that pass through its center. These symmetries are important in geometry and can be useful in various applications, such as in design and architecture.
Shapes with 90 Degree Rotational Symmetry
Shapes that have 90-degree rotational symmetry are those that can be rotated by a quarter turn (90 degrees) and still look the same as they did before the rotation. Square, rectangle, and diamond are some examples of shapes that have 90-degree rotational symmetry. These shapes have four equal sides and four right angles, which means that they can be rotated by 90 degrees without changing their appearance. Other shapes that have 90-degree rotational symmetry include regular polygons like octagons and hexagons. In contrast, shapes such as triangles and circles do not have 90-degree rotational symmetry because they do not look the same after a quarter turn rotation.
Are Rectangles Always 90 Degrees?
A rectangle always has four right angles measuring 90 degrees each. This is one of the defining properties of a rectangle. A rectangle is a quadrilateral with opposite sides that are parallel and congruent, and all four interior angles are 90 degrees. This means that the opposite sides of a rectangle are equal in length, and the adjacent sides are perpendicular to each other. The presence of these right angles is what makes a rectangle different from other quadrilaterals such as a parallelogram or a trapezoid. So, to answer the question, a rectangle is indeed always 90 degrees.
Symmetry of a Rectangle
A rectangle has several types of symmetry. First, it has two lines of symmetry, one vertical and one horizontal, which means that it can be folded in half along either of these lines and the two halves will perfectly match. Additionally, a rectangle also has rotational symmetry of order two, which means that if it is rotated 180 degrees around its center point, it will still look the same. a rectangle exhibits both reflective symmetry and rotational symmetry, making it a symmetrical shape in multiple ways.
Examples of Rotational Symmetry
Rotational symmetry is a type of symmetry that occurs when a figure can be rotated around its center point by a certin angle and still appears the same. A classic example of a figure with rotational symmetry is a regular polygon, such as a square, triangle, or hexagon. For instance, a square has rotational symmetry of order 4 since it can be rotated 90 degrees, 180 degrees, or 270 degrees and still look the same. In contrast, a rectangle does not have rotational symmetry because it changes shape if it is rotated. Other examples of figures with rotational symmetry include circles, stars, and snowflakes. rotational symmetry is a fascinating concept that plays a crucial role in various fields, such as geometry, art, and design.
Rotational Symmetry of a Circle
A circle is a rotational symmetry. It has an infinite number of angles of symmetry, meaning that if you rotate it by any angle around its center, it will look exactly the same as it did before the rotation. This is because all points on the circle are equidistant from the center, so rotating the circle does not change its shape or position. Additionally, the order of the rotation symmetry of a circle is infinite, meaning that it can be rotated an infinite number of times and still look the same.
Understanding the Concept of Rotational Shapes
A rotational shape is a two-dimensional figure that is moved around a fixed point by a certan angle, either clockwise or anticlockwise. The shape retains its original size and proportions, but its position in space changes. The fixed point is called the center of rotation, and the angle of rotation is measured in degrees. Rotational shapes can be any polygon, such as a triangle, square, or pentagon, or even irregular shapes. The concept of rotational symmetry is also related to rotational shapes, where a figure can be rotated by a certain angle and still look the same. Rotational shapes are used in many areas of mathematics and physics, including geometry, trigonometry, and mechanics.
Does Every Object Possess Rotational Symmetry?
Rotational symmetry is a property of an object that describes the ability of the object to appear the same after a certain amount of rotation around a fixed point. The answer to the question of whether every object has rotational symmetry is not straightforward and depends on the shape and features of the object.
Some objects have rotational symmetry, which means that they look the same after rotating them around a fixed point by a certain angle. For example, a regular hexagon has rotational symmetry of order 6, which means that it loos the same after rotating it by 60 degrees, 120 degrees, 180 degrees, 240 degrees, 300 degrees, and 360 degrees. Similarly, a circle has rotational symmetry of infinite order because it looks the same after any amount of rotation.
However, not all objects have rotational symmetry. For example, irregular shapes like a rock or a tree do not have rotational symmetry. Also, some shapes may only have rotational symmetry of order 1, which means that they look the same after rotating them by 360 degrees.
Whether an object has rotational symmetry or not depends on the shape and features of the object. Some objects have rotational symmetry, while others do not.

Conclusion
A rectangle is a geometric shape that has several symmetrical properties, making it a fundamental shape in mathematics. It has two lines of symmetry and rotational symmetry of order two, which means that it looks the same when rotated 180 degrees. Additionally, a rectangle has reflectional symmetry when reflected over the line through the midpoints of its opposite sides. Its symmetrical properties make it a usful shape for many practical applications, such as in construction and design. Understanding the properties of a rectangle is essential in solving problems related to geometry, and it lays the foundation for learning more complex shapes and concepts.
