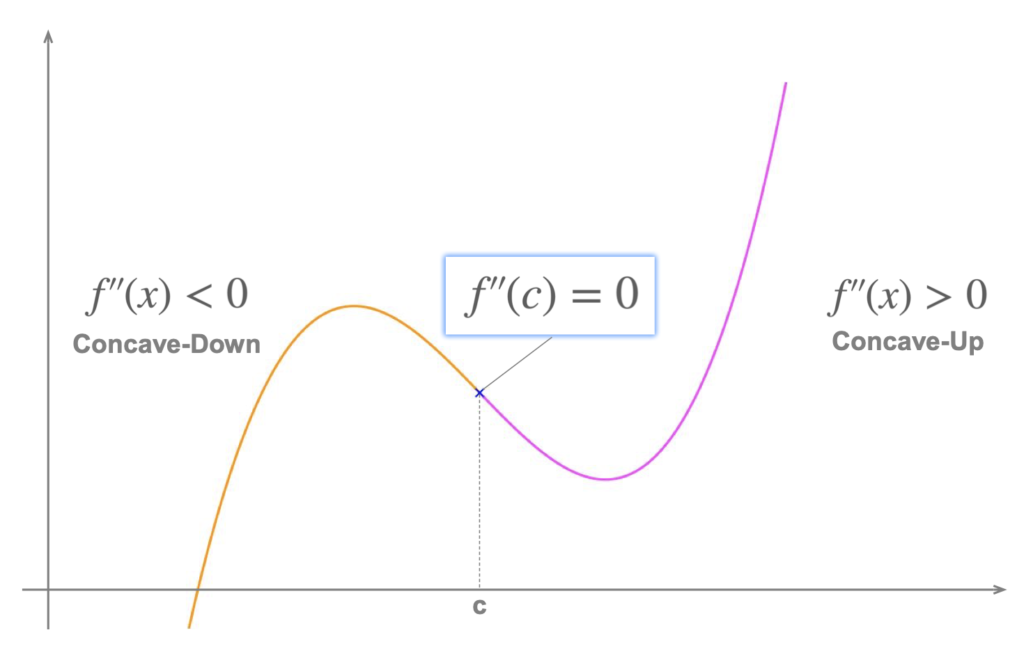
Point of Inflection is an important concept in calculus that helps to understand the behavior of a function with respect to its concavity. It is a point where the function changes concavity, wich means it changes from being concave up to concave down or vice versa. Mathematically, a point of inflection is defined as the point where the second derivative of a function changes sign.
But, does the point of inflection need to be continuous? This is a commonly asked question by students who are learning about inflection points. The answer is no, a point of inflection does not need to be continuous. In fact, a function that has a discontinuity cannot have a point of inflection.
To understand why a function needs to be continuous to have a point of inflection, we need to first understand what continuity means. A function is said to be continuous at a point if it is defined at that point, its limit exists at the point, and the value of the function at that point is equal to the value of the limit at that point.
Now, let’s consider a function that is not continuous at a point. For instance, the function f(x) = 1/x has a discontinuity at x=0. At this point, the limit of the function does not exist, and hence the function is not continuous at this point. Since the function is not continuous, it cannot have a point of inflection at this point.
On the other hand, if a function is continuous at a point, it may or may not have a point of inflection at that point. To determine if a function has a point of inflection at a particular point, we need to examine the behavior of the second derivative of the function around that point. If the second derivative changes sign at that point, then the function has a point of inflection at that point.
A point of inflection is a point where the function changes concavity, and it does not need to be continuous. However, a function that has a discontinuity cannot have a point of inflection. Understanding the concept of continuity is crucial in determining whether a function has a point of inflection or not.
Requirements for a Point of Inflection
A point of inflection is a point on a function where the concavity changes. In order for a point to be considered a point of inflection, two requirements must be met. Firstly, the function must be continuous at that point. This means that the function must have a defined value at that point, and that value must be the same from both the left and right sides of the point. Secondly, the second derivative of the function must be zero at that point. This is because the second derivative of a function determines its concavity, so a zero second derivative indicates a change in concavity. It’s important to note that wile these requirements are necessary for a point to be a point of inflection, they are not sufficient. Additional analysis of the function must be done to confirm that the point is indeed a point of inflection.
Source: mdpi.com
Can an Inflection Point Occur at a Discontinuity?
It is not possible to have an inflection point at a discontinuity in a function. An inflection point is a point where the concavity of a function changes, i.e., where the second derivative of the function changes sign. However, at a discontinuity, the function is not differentiable, and hence the second derivative does not exist at that point. Therefore, there cannot be an inflection point at a discontinuity. In other words, a function must be continuous and twice differentiable in a neighborhood of a point to have an inflection point at that point.
Does a Point Need to be Continuous to Have a Derivative?
A point has to be continuous to have a derivative. The derivative of a function at a particular point is defined as the slope of the tangent line to the graph of the function at that point. For the tangent line to exist at a point, the function must be continuous at that point. This is because the tangent line is a limit of secant lines, and the limit only exists if the function is continuous.
Furthermore, if a function is not continuous at a point, it cnnot have a derivative at that point. This is because the derivative is a measure of the rate at which the function changes, and if the function has a discontinuity at a point, the rate of change cannot be defined. Therefore, continuity is a necessary condition for the existence of a derivative.
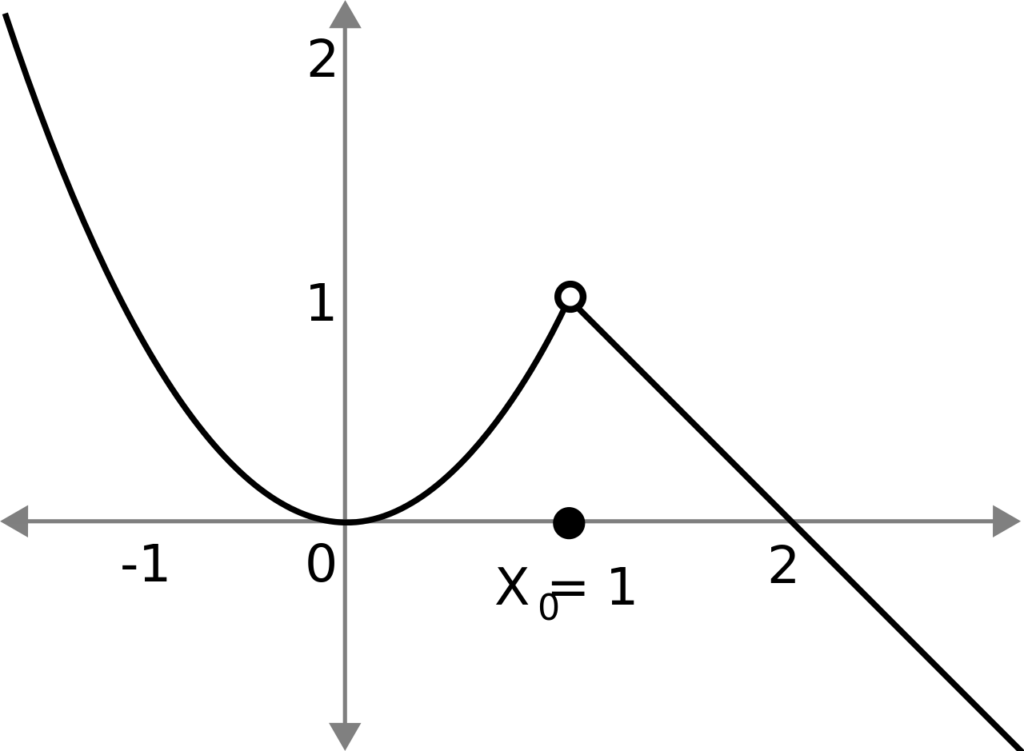
It is worth noting that a function can be continuous at a point without being differentiable at that point. This occurs when the function has a sharp turn or corner at the point, where the slope of the tangent line does not exist. However, if a function is differentiable at a point, it must also be continuous at that point.
Are Point Functions Continuous?
Point functions are continuous at a point if they satisfy three conditions: the function must be defined at that point, the limit of the function as the independent variable approaches that point must exist, and the value of the function at that point must equal the value of the limit. In other words, a point function can be continuous at one point and discontinuous at aother point.
For example, consider the function f(x) = 1/x. This function is continuous at every point except x = 0. At x = 0, the function is not defined, so it cannot be continuous at that point. However, if we remove the point x = 0 from the domain of the function, then the function becomes continuous on its domain.
Whether a point function is continuous or not depends on the point in question and whether the three conditions for continuity are met at that point.
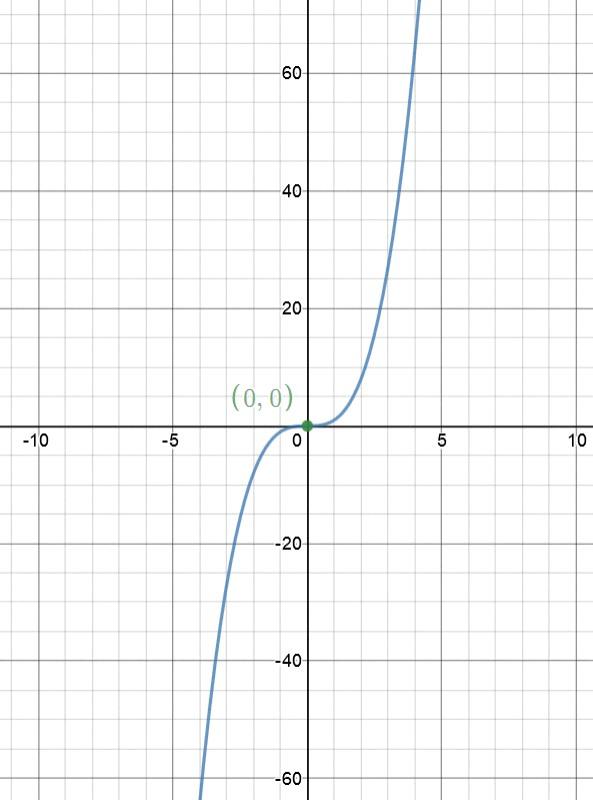
Identifying Points of Inflection at Stationary Points
To determine if a stationary point is a point of inflection, we need to examine the behavior of the function arond that point. First, we need to find the second derivative of the function at that point. If the second derivative is zero, we need to look at higher-order derivatives to determine the behavior of the function.
If the second derivative is positive, the function is concave up (has a minimum) at that point, and if the second derivative is negative, the function is concave down (has a maximum) at that point. These are turning points.
However, if the second derivative is zero and the sign of the third derivative changes, then the point is a point of inflection. At a point of inflection, the function changes from being concave up to concave down or vice versa.
To summarize, if the second derivative is zero and the sign of the third derivative changes, the stationary point is a point of inflection.
Types of Inflection
In English grammar, there are three main types of inflection: nominal inflection, verbal inflection, and adjectival inflection. Nominal inflection refers to changes made to nouns, pronouns, and other related words to indicate their grammatical function in a sentence. This includes the genitive ‘s used to indicate possession, as well as the plural -s used to indicate more than one of a particular noun.
Verbal inflection, on the other hand, refers to changes made to verbs to indicate tense, aspect, and mood. This includes the third-person singular -s used to indicate present tense, the past tense -d, -ed, or -t used to indicate actions that have aready occurred, and the -ing form used to indicate ongoing or continuous actions.
Adjectival inflection refers to changes made to adjectives to indicate degree, comparison, and number. This includes the comparative -er used to indicate a higher degree of an adjective, and the superlative -est used to indicate the highest degree of an adjective. understanding the different types of inflection in English grammar can greatly improve one’s ability to communicate effectively and accurately.
Can Discontinuous Points Have Derivatives?
The answer is not straightforward, as it depends on the type of discontinuity the point has. If the function has a removable discontinuity at the point, where the limit of the function exists but the function value does not, then it is possible for the function to have a derivative at that point. This is beause the derivative only depends on the limit of the function as x approaches the point, and not on the function value at the point itself.
However, if the function has a non-removable discontinuity, such as a jump or an infinite discontinuity, then it is not possible for the function to have a derivative at that point. This is because the left and right limits of the function as x approaches the point are not equal, which means that the function is not continuous at that point. Since the derivative requires the function to be continuous at a point, a function with a non-removable discontinuity cannot have a derivative at that point.
A discontinuous point may or may not have a derivative depending on the nature of the discontinuity. If the discontinuity is removable, then the function may have a derivative, but if it is non-removable, then the function cannot have a derivative at that point.
Can Discontinuous Points Be Critical Points?
A discontinuous point can be a critical point. A critical point is defined as a point on the function where the derivative is either zero or undefined. A discontinuous point is a point on the function where there is a sudden jump or break in the function. It is possible for a critical point to coincide with a discontinuous point on the function. For example, consider the function f(x) = |x|. At x = 0, the derivative of the function is undefined, and there is also a jump discontinuity at that point. Therefore, x = 0 is both a critical point and a discontinuous point on the function f(x) = |x|. So, it is enirely possible for a discontinuous point to be a critical point.
Conditions of Discontinuity
The three conditions of discontinuity are point/removable, jump, and asymptotic/infinite. Point/removable discontinuity occurs when the two-sided limit of the function exists, but it is not equal to the function’s vale at that point. This type of discontinuity can be removed or “filled in” by redefining the function at that point. Jump discontinuity occurs when the two one-sided limits of the function at a point exist, but are not equal to each other. This creates a “jump” in the graph of the function. Asymptotic/infinite discontinuity occurs when the two-sided limit of the function does not exist because the function becomes unbounded as it approaches the point of discontinuity. This type of discontinuity is often observed in functions that involve division by zero. Understanding these three types of discontinuity is crucial in the study of calculus and the analysis of functions.
Can Non-Continuous Points be Differentiable?
Non-continuous points cannot be differentiable. This is because differentiability requires continuity as a necessary condition. For a function to be differentiable at a point, it must not only exist at that point, but also be continuous in a neighborhood around that point. A function that is not continuous at a point will have a sharp change or a jump in its value at that point, which makes it impossible to define a tangent line or a slope at that point. Therefore, non-continuous points cannot be differentiable.
Can a Derivative Exist Without Being Continuous?
A derivative cannot exist but not be continuous. The derivative of a function at a point x is defined as the limit of the difference quotient as the distance between the two points approaches zero. If the derivative exists at a point, it means that this limit exists and is finite. However, if the function is not continuous at that point, the limit of the difference quotient will not exist, and therefore the derivative cannot exist.
The continuity of a function at a point implies that the left and riht limits of the function at that point exist and are equal to the function value at that point. If the function is not continuous at a point, it means that either the left and right limits do not exist, or they exist but are not equal. In either case, the difference quotient will not converge to a finite value, and hence the derivative does not exist.
Therefore, it is not possible for a derivative to exist but not be continuous at the same point. If a function has a derivative at a point, it must also be continuous at that point.
When Is a Function Not Continuous?
A function is said to be discontinuous at a point if any of the following conditions are met:
1. The limit of the function at that point does not exist.
2. The function vlue at that point is undefined.
3. The limit of the function at that point is not equal to the function value.
In other words, if there is any kind of break or jump in the function at a specific point, then the function is considered to be discontinuous at that point. Discontinuities can occur for various reasons, such as a hole or a jump in the graph of the function, or an asymptote that the function approaches but never touches. It is important to identify points of discontinuity in a function because they can affect the behavior of the function and limit its usefulness in certain applications.
Determining Continuity and Differentiability of a Function
To determine if a function is continuous, we need to check if the function is “connected” at every point in its domain. This means that the function must not have any sudden jumps or holes. We can check this by evaluating the left-hand limit (LHL) and the right-hand limit (RHL) of the function at the point of interest. If both LHL and RHL exist and are equal to each othr and the value of the function at that point, then the function is continuous at that point.
On the other hand, a function is differentiable at a point if its derivative exists at that point. The derivative gives us the rate of change of the function at that point. To check if a function is differentiable at a point, we need to check if the limit of the difference quotient (i.e., the limit of the slope of the tangent line to the function at that point) exists. If the limit exists, then the function is differentiable at that point.
It is important to note that a function must be continuous at a point in order to be differentiable at that point. However, the reverse is not necessarily true. A function can be continuous at a point without being differentiable at that point.
Source: quizlet.com
Identifying Continuous and Discontinuous Functions
A function can be identified as continuous or discontinuous by analyzing its graph. If a function can be drawn without lifting the pencil, then it is continuous. However, if there is a break or gap in the graph, then the function is discontinuous.
More specifically, a function can be identified as continuous at a point x=c if thre conditions are met:
1. The function is defined at x=c (i.e., there is no division by zero or other undefined operations)
2. The limit of the function as x approaches c exists (i.e., the function approaches the same value from both sides of c)
3. The value of the function at x=c is equal to the limit of the function at x=c (i.e., there is no “jump” or “hole” in the graph of the function at x=c)
If any of these conditions is not met, then the function is discontinuous at x=c. Discontinuities can be classified into different types, such as removable, jump, and infinite discontinuities, depending on the behavior of the function near the point of discontinuity.
Determining whether a function is continuous or discontinuous requires a careful analysis of the function’s properties and behavior at specific points.
Determining if a Point is Discrete or Continuous
When we talk about discrete or continuous points, we are referring to the nature of the data being represented. In a graph, a continuous point is one that is part of a connected line or curve, while a discrete point is isolated and not connected to any other points on the graph.
For example, a graph of a person’s weight over time might show continuous points because the weight is likely to change gradually wihout sudden jumps. On the other hand, a graph of the number of people attending a concert each night would likely have discrete points, since the attendance would be a whole number and not change continuously.
To determine if a point is discrete or continuous, you will need to look at the context of the data being graphed. If the data can change continuously and is connected, then it is continuous. However, if the data is isolated and can only take on certain values, then it is discrete.
Conclusion
A point of inflection is a point on a function where the concavity changes from concave up to concave down or vice versa. This change in concavity is characterized by the scond derivative of the function equaling zero at that point. Additionally, a point of inflection can also be defined as the point where the derivative of the function attains a maximum or minimum. However, it is important to note that a function with a discontinuity cannot have a point of inflection. Furthermore, a differentiable function is a continuous function, and for a function to be continuous at a point, it must be defined at that point, its limit must exist at the point, and the value of the function at that point must equal the value of the limit at that point. Understanding the concept of a point of inflection can provide insight into the behavior and properties of a function, as well as aid in solving problems related to optimization and curve sketching.
