Are you looking to learn more about degrees of freedom (DF) in statistics? If so, you’ve come to the right place! Degrees of freedom (DF) is an important concept that is often used in various forms of hypothesis testing, such as a chi-square. In this blog post, we’ll take a closer look at what DF is, how it’s calculated, and why it’s so important.
So what is DF? Put simply, it is the number of independent pieces of information used to calculate a statistic. This number can be calculated by subtracting one from the sample size. For example, if you have five items in your sample data set, then your degree of freedom would be four (5-1 = 4).
DF plays an important role when it comes to hypothesis testing. This is because it helps to determine the level of variance within a set of data. For example, if you were analyzing data from a normal distribution, then the degrees of freedom would be used to calculate the variance for each quantity. To do this, you would first need to calculate the Sums of Squares (SStr and SSE) and then divide them by their corresponding DF to get Mean Squares (MStr and MSE).
In addition to being used in hypothesis testing, DF can also be used when determining statistical significance. Specifically, if there are fewer degrees of freedom within a set of data then there will be less uncertainty as to whether or not any observed difference between two groups was due solely to chance or not.
In summary, degrees of freedom (DF) is an important concept that helps us understand how much variance exists within a given data set. It plays an essential role in various forms of hypothesis testing and can also help us determine statistical significance when analyzing two groups for differences between them. Hopefully this blog post has helped prvide some more insight into what DF is and why it’s so important!
Understanding the Meaning of ‘DF’ in Statistics
In statistics, the term df (or degrees of freedom) refers to the number of independent pieces of information used to calculate a statistic. It is calculated as the sample size minus the number of restrictions. For example, if you have a sample size of 10 and two restrictions, then thee are 8 degrees of freedom in your data set.
The concept of degrees of freedom can be applied to different statistical methods such as t-tests, ANOVA, and regression analysis. In each case, the df is used to determine the level of precision with which you can interpret your results. Generally speaking, the higher your degree of freedom, the more reliable your results will be.
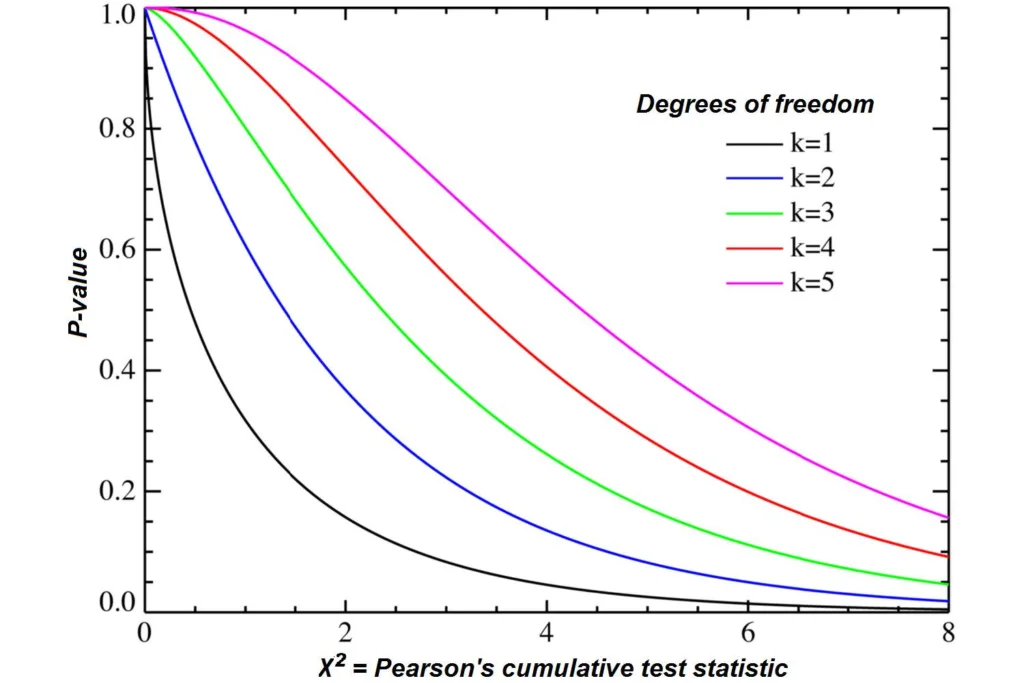
Calculating Degrees of Freedom
To calculate the degrees of freedom (df), you must first determine the number of items in your data sample. Once you have that information, subtract one from that number to get the df. For example, if your sample contains 10 items, then the degrees of freedom would be 9 (10 – 1 = 9). Degrees of freedom are an important concept in statistics and hypothesis testing, such as a chi-square test. It helps to determine how reliable the results of a statistical test may be.
Understanding the Meaning of ‘DF’ in Standard Deviation
Degrees of freedom (df) in standard deviation refers to the number of independent observations that are used in computing the statistic. It is the number of data points minus one (n-1). For example, if we have 10 data points, then df = 10-1 = 9. The df value is important because it influences the standard deviation calculation, as the larger the df value, the smaller the standard deviation will be. In oher words, when estimating statistics from a normal distribution using a sample size of n observations, df should be set to n-1. The greater the sample size is, the more accurate our estimation will be; however, if we have too few degrees of freedom, our estimates may not be as reliable.
Understanding the Meaning of DF in Statistics ANOVA
In statistics, ANOVA (Analysis of Variance) is a method for examining the relationship between multiple variables. The degrees of freedom (DF) are used to calculate the mean squares in ANOVA which are used to test whether there is a significant difference between the means of two or more groups. Degrees of freedom in statistics can be thought of as the number of independent pieces of information that go into calculating a statistic.
For example, when conducting an ANOVA, the total sum of squares (SST) is calculated by subtracting the grand mean from each individual observation and then squaring and summing each difference. This requires knowledge of each individual observation, and thus has n-1 DF, where n is the total number of observations. Similarly, in order to calculate the sum of squares due to treatment (SSTr), we need to know how much each group differs from its own mean, which requires k-1 DFs, where k is the number of treatment groups.
These DFs are then used to calculate the Mean Squares for Total and Treatment respectively. The Mean Square for Total (MST) is equal to SST divided by its corresponding degrees of freedom (n-1). Similarly, the Mean Square for Treatment (MStr) is equal to SStr divided by its corresponding degrees of freedom (k-1). Finally, thse two values are used in F-test calculations which allow us to determine if there is a significant difference between treatments or not. Therefore, DFs in ANOVA are an important part of conducting a valid analysis.
Understanding the DF Value in Regression
The df value in regression is the number of independent variables used to estimate the model. In this example, our regression model only uses GRE scores, so it has one df (1). The residual df is the total number of observations (rows) in the dataset minus the number of variables being estimated. Therefore, for this example it would be the total number of observations in the dataset minus 1 (the variable being estimated), giving us a residual df of n-1.
Source: stats.stackexchange.com
Degrees of Freedom: N1 or N2?
No, the degrees of freedom is not n-1 or n-2. The degrees of freedom for a correlation test is alwas equal to n-2, where n is the number of data points in the sample. This means that if you have 10 data points, then the degrees of freedom is 8. This is because when you calculate a correlation coefficient, you are actually taking into account two variables (x and y) and each variable has one degree of freedom (because it can take any value). Therefore, when you subtract two degrees of freedom from the total number of samples, you get the correct number of degrees of freedom for a correlation test.
Calculating the Degrees of Freedom for an F Test
The degree of freedom (df) in an F test is calculated by subtracting 1 from the number of samples used in the test. For example, if you are conducting an F test with two samples, the df would be calculated as follows: df1 = n1 – 1 and df2 = n2 – 1, where n1 and n2 are the sample sizes. Therefore, if you have two samples of 10 each, then your df would be 9 for each sample. This means that when loking up critical values in an F table for a two-tailed test, you would need to divide your alpha by 2 to get the correct critical value.
Understanding the Meaning of DF in Confidence Interval
DF, or degrees of freedom, in a confidence interval refers to the number of independent observations in a sample. DF is equal to N – 1, whre N is the sample size. In other words, if you have a sample size of 10, then the degrees of freedom would be 9. The df value is used in determining the t-value for a confidence interval. The t-value and df are then used to calculate the confidence interval for the mean with a given level of confidence (usually 95%). By using the t-table or an inverse t distribution calculator, you can determine what t-value corresponds to your df and desired level of confidence.
Finding the Degrees of Freedom in a Hypothesis
The degrees of freedom (DF) for a hypothesis are determined by the number of independent variables in the data set. For example, if you have a two-tailed hypothesis test with two independent variables, the DF would be 2-1 = 1. If you have a three-tailed hypothesis test with three independent variables, the DF would be 3-1 = 2. The DF should always be equal to one less than the number of independent variables in the data set. Once the DF is calculated, it can then be used to calculate the critical value for rejecting or accepting the null hypothesis.
The Importance of Data Fusion in Data Analysis
Degrees of freedom (DF) is a measure of how much freedom an analysis has to vary without running afoul of certain constraints. It is an essential concept in statistics and is used in hypothesis tests, probability distributions, and linear regression. DF is important because it allows us to assess the validity of our data and calculations by ensuring that our assumptions about the data are met. By understanding DF, we can also better evaluate the statistical significance of our results. Additionally, by taking into account DF, we can determine the reliability of our conclusions when uing a variety of analytical techniques. In short, knowing and understanding the degree of freedom helps us make more informed decisions based on our data analyses.
Interpreting a High Degree of Freedom in Statistics
A high degree of freedom (DF) in statistics means that the sample size is large. This usually results in increased power to reject a false null hypothesis and find a significant result. With larger sample sizes, it’s easier to detect subtle differences between two groups or variables, as well as to make more accurate estimates about population parameters. In addition, larger sample sizes provide more reliable data for statistical tests and enable researchers to use more complex models and analyses. As such, higher degrees of freedom typically lead to more robust and reliable findings.
The Meaning of DF in T-test
DF in t-test stands for Degrees of Freedom. It is a measure of the number of values or observations that are free to vary within a given sample dataset. The degrees of freedom value is used to calculate the statistic in the t-test, which helps to determine if there is a statistically significant difference between two sets of results. The degrees of freedom value is equal to the sample size minus one, so if you have 10 data points, your degree of freedom would be 9.
Understanding Degrees of Freedom and F-Values in ANOVA
DF and F are two related concepts in Analysis of Variance (ANOVA). DF stands for “degrees of freedom,” whih is the number of values within a dataset that can vary independently. DF is important in ANOVA because it affects the significance level of the results. The F-statistic, or F, is a measure of the strength of the relationship between two or more variables. It is calculated by dividing the Mean Square Between (MSB) by the Mean Square Within (MSW), and can be used to determine whether there is a statistically significant association between two or more variables. F has a higher value when there is a strong relationship between variables, and a lower value when there is no significant relationship.
Calculating Degrees of Freedom (DF) From ANOVA
To calculate degrees of freedom (DF) for ANOVA, you first need to determine the number of groups within your study. Once you have determined the number of groups, subtract 1 from that number to calculate the degrees of freedom between groups. Then, subtract the number of groups from the total number of subjects to calculate the degrees of freedom within groups. Finally, subtract 1 from the total number of subjects (values) to find total degrees of freedom. For example, if you have four groups and a total of 30 subjects, your calculations would look like this: DFbetween = 4 – 1 = 3; DFwithin = 30 – 4 = 26; DFtotal = 30 – 1 = 29.

Understanding the Meaning of DF in SPSS
DF (degrees of freedom) in SPSS refers to the number of observations that are free to vary without any constraints. When performing statistical tests in SPSS, DF is used to calculate the statistical significance of a result. For example, when using a single sample t-test, DF is equal to the number of valid observations minus 1, since we have estimated the mean from the sample. It is important to remember that the higher the degrees of freedom, the more likely it is that a result will be statistically significant.
Conclusion
In conclusion, degrees of freedom (df) is an important concept in statistics that helps to determine the number of independent pieces of information used to calculate a statistic. It is calculated by subtracting one from the number of items within the data sample and is commonly abbreviated to df. This concept has been used in various forms of hypothesis testing such as a chi-square, and it is also used in ANOVA analysis where the Sums of Squares are divided by corrsponding DF to get the Mean Squares. Degrees of freedom is an essential concept for anyone wanting to understand and use statistics properly, as it helps to ensure that accurate results are obtained.
