Cosecant, or csc, is a trigonometric function that is the reciprocal of sine. In other words, it is the inverse of sine. It is used to calculate angles and lengths in right triangles and has many applications in physics and engineering.
The cosecant of an angle ‘θ’ can be calculated by taking the reciprocal of the sine of that angle. Mathematically, csc θ = 1/sin θ. This means that if we know the value of one side in a right triangle, then we can determine the other two sides using cosecant.
For example, if we know the length of one side (say ‘a’) and an angle (say ‘θ’), then we can use cosecant to calculate the other two sides (b and c). We can do this by using the following equation:
b = a*csc θ and c = a*cot θ
Where ‘a’ is the known side length, b is the opposite side length and c is the adjacent side length. This equation works because it takes advantage of both sine and cosine functions – which are related to each other through their reciprocals.
In addition to being used in calculating angles and lengths in right triangles, cosecant also has applications in calculus where it can be used to differentiate trigonometric functions as well as solve equations involving derivatives or integrals. Cosecant also appears frequently in physics problems where it is often used to analyze wave motion or calculate energy levels witin an atom.
Overall, understanding how to use cosecant can be incredibly useful for anyone studying mathematics, physics or engineering. By mastering this concept you will be able to more accurately calculate angles and lengths as well as solve more complex equations with ease!
Inverse Relationship Between Cos and Csc
No, csc (cosecant) is not the inverse of cos (cosine). The inverse of a trigonometric function is the same function, except that its argument or input is inverted or reversed. The inverse of cos (cosine) is arccos (inverse cosine), which takes the output of cos and reverses it to figure out what angle produced that output. However, csc (cosecant) is the reciprocal of sin (sine), not cos. That means that csc takes the output of sin and reverses it to figure out what angle produced that output.
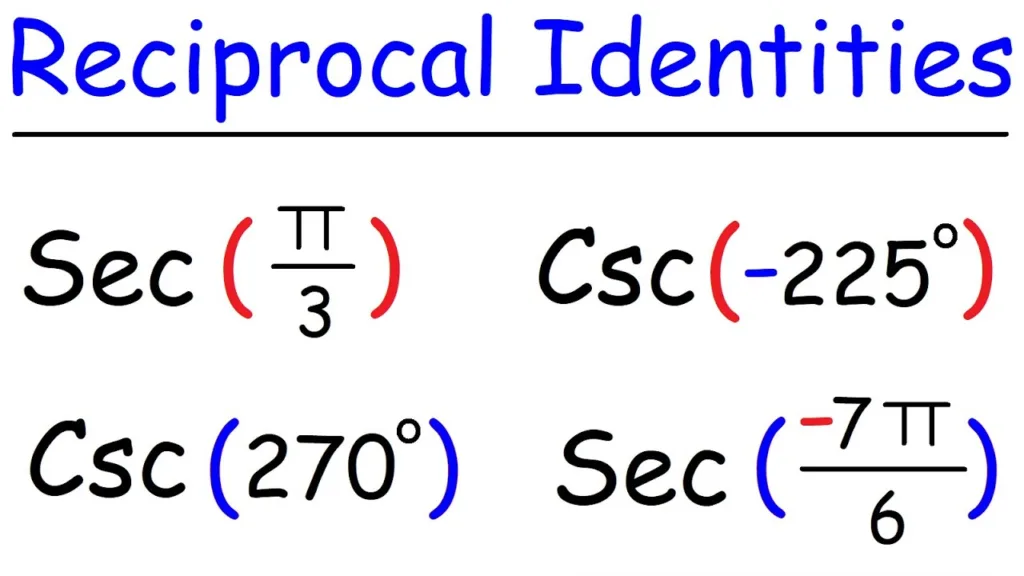
What Does Csc Stand For?
The cosecant of x (csc x) is equal to 1 divided by the sine of x. In other words, it is the reciprocal of the sine of x. The formula for cosecant is csc x = 1 sin x. This means that if we know the value of the sine of an angle, then we can calculate its cosecant simply by taking the reciprocal. For example, if we know that sin(x) = 0.5, then csc(x) = 1/0.5 = 2.
What is the Reciprocal of Sin CSC?
Yes, the reciprocal of sin is cosecant, which is abbreviated as csc. Cosecant is the inverse trigonometric function of sine and can be expressed as csc(θ) = 1/sin(θ). This means that given a known angle θ, you can use cosecant to determine the ratio of the opposite side of a right triangle to its hypotenuse.
The Reciprocal of 1 Csc
The reciprocal of 1 csc is simply the inverse of csc, which is equal to sin. Put another way, 1 csc = 1/sin(x). The reciprocal of 1 csc can be written as sin(x).
Is the Cosecant of 1 Equal to the Cosine of 1?
No, csc (cosecant) is not equal to cos (cosine) 1. They are two different functions and should not be confused. Cosecant is the reciprocal of sine, while cosine is the ratio of an angle’s adjacent and hypotenuse sides in a right triangle. Therefore, csc (1) would be equal to the reciprocal of sin (1), which is 1/sin(1), not cos(1).
The Relationship Between Sin 1 and Csc
No, sin 1 and csc are not the same. Sin 1 (or sinx) is the trigonometric function that measures the ratio of the side opposite the angle to the hypotenuse in a right triangle. Csc (or cosecant) is the multiplicative inverse (or reciprocal) of this function, which means that its value is equal to 1 divided by the value of sin x.
The Equivalent of Csc θ
The equivalent of csc θ is the inverse of the sine function, which is denoted by cosecant. Cosecant is written as csc(θ) and it is defined as 1/sin(θ). In other words, it is the reciprocal of the sine function, meaning that it takes the sine value and flips it around to find its inverse. For example, if we take a look at a right triangle and measure the angle θ, then we can use cosecant (csc(θ)) to calculate the ratio of the side opposite to θ divided by the hypotenuse.
The Reciprocal of Cosec θ
The reciprocal of Cosec θ is the Sine θ function. The sine function is a trigonometric function that takes an angle as an argument and returns the ratio of two sides of a riht triangle. The cosecant of an angle is defined as the reciprocal of the sine of that same angle, so if you know the cosecant of an angle, you can find its sine by taking the reciprocal. To calculate the sine of an angle, you need to know its measure in radians or degrees. In radian measure, the formula for finding the sine is sin(θ) = opposite/hypotenuse. In degree measure, use a scientific calculator and enter Sin (θ).
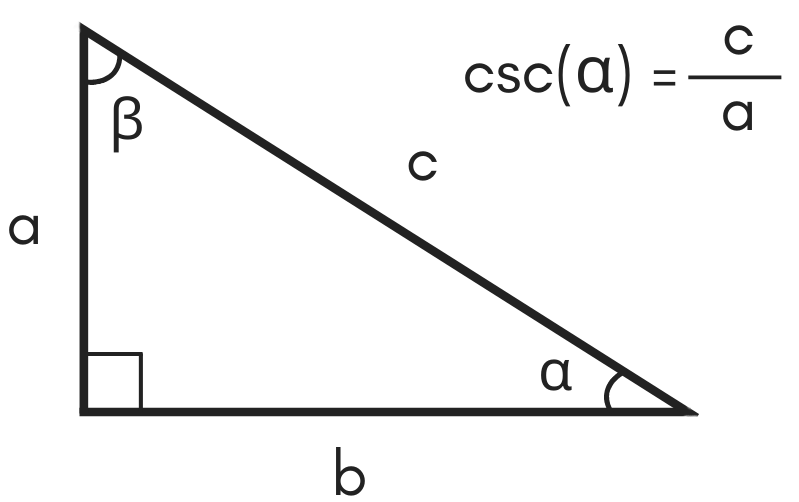
The Relationship Between Csc and Hypotenuse
No, the cosecant is not opposite over hypotenuse. The cosecant is given by the ratio “hypotenuse over opposite”. This means that the cosecant is equal to the length of the hypotenuse divided by the length of the side opposite it in a right triangle. By contrast, the cotangent is given by the ratio “adjacent over opposite”, which means that it is equal to the length of the side adjacent to an angle divided by the length of its opposite side.
Conclusion
In conclusion, cosecant is the reciprocal of sine, and its abbreviation is csc. It can be calculated by flipping the sin over, and it is important to remember that cosecant and secant are reciprocals of each other. Cosecant is a useful tool for measuring angles in trigonometry, and can help to solve many mathematical equations.
