Hello everyone! Today we’re going to be discussing binormal vectors and their equations. A binormal vector is a line that is perpendicular to both the normal and the tangent of a point on a curve and, together with them, forms thee orthogonal axes.
In order to understand binormal vectors, let’s first examine vector-valued functions. A vector-valued function is a function whose range or output values are multi-dimensional vectors. Such a function can be written as r(t) where t is an independent variable. The velocity vector of this function can then be written as v(t)=r′(t). We can then define the unit tangent vector by tˆi+etˆj−3t2ˆk where the three orthogonal components represent the x, y and z axes in 3D space respectively.
The binormal vector equation is then expressed as B=T×N where T represents the unit tangent vector and N represents the normal vector which is perpendicular to the unit tangent (T). This equation means that when you have two mutually perpendicular vectors (T and N), their cross product gives you another mutually perpendicular vector (B), which will be the binormal vector.
To illustrate this concept graphically, imagine tracing a curved path along an imaginary surface in 3D space using your finger as if it was a pen drawing on paper. As you move along this path, your finger will always point in one direction like an arrow indicating the direction of movement – this arrow is known as the unit tangent vector T. The normal at any point on this path will be perpendicular to T at that point in 3D space – this normal is known as N. Finally, when you take their cross product, you get yet another mutually perpendicular vector called B which represents our binormal vector equation of B = T × N
We hope this blog post has given you some insight into binormals vectors and their equations!
The Significance of the Binormal Vector
The binormal vector is a vector that is normal to both the tangent vector and the normal vector of a curved path. It points in the direction of the maximum rate of change in curvature and can be used to define the osculating plane. This plane is essentially an imaginary surface that passes through a point on the curve, with its orientation determined by the binormal vector. It contains all vectors (e.g., velocity, acceleration, force) that are tangent to the curve at that particular point, and is therefore useful for characterizing motion along a curved path.
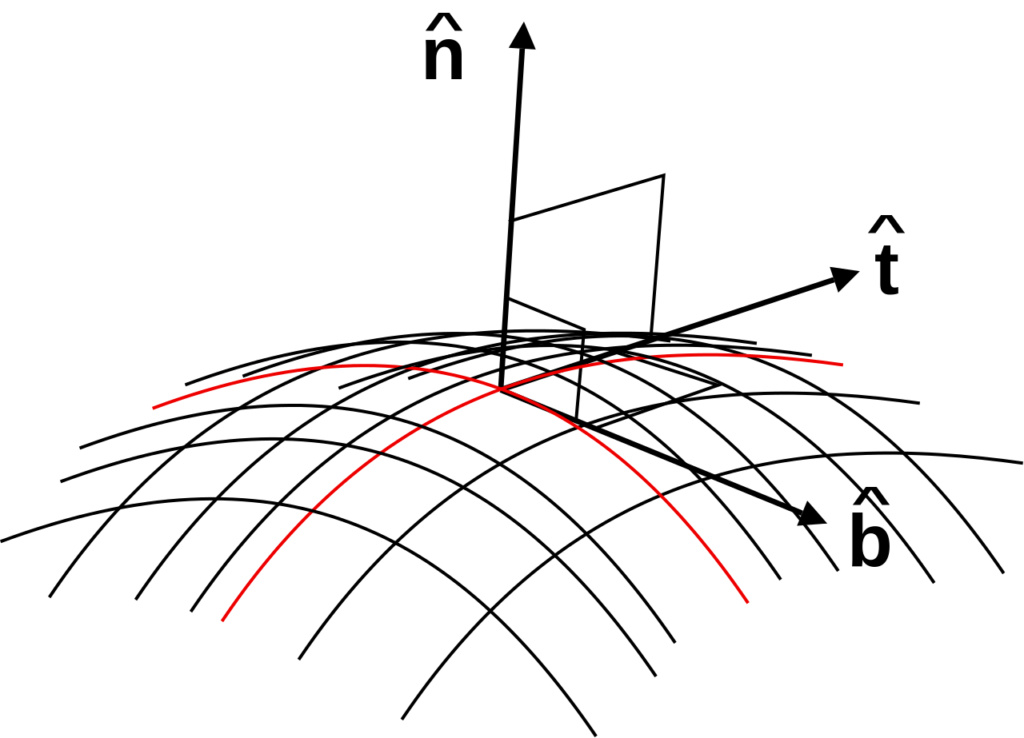
What is Binormal Mathematics?
Binormal math is a branch of mathematics that deals with the properties of a point on a curve. It is based on the concept of three orthogonal axes: the normal, tangent and binormal. The normal is a line that is perpendicular to the curve at any given point. The tangent is a line that touches the curve at any given point and points in the direction of its greatest rate of change. The binormal, which is also sometimes referred to as “the bitangent”, is a line that forms an angle of 90 degrees with both the normal and tangent lines. In oter words, it is at right angles with both of them.
The binormal has several uses in mathematics, including describing properties such as curvature and torsion at any point on a curve or surface. It can also be used to calculate equations such as acceleration and speed along curves, or to measure how far away two objects are from each other in 3-dimensional space. Binormal math can also help us understand how forces interact along curved surfaces and how light behaves as it reflects off curved surfaces.
Equation for a Tangent Vector
The equation for a tangent vector, t(t), is given by the unit vector in the direction of the velocity vector v(t). That is, t(t) = v(t)/|v(t)|, where |v(t)| is the magnitude of v(t).
In this case, since r'(t) = (1, e, -3t), we can calculate the magnitude of r'(t): |r'(t)| = sqrt((1)^2 + (e)^2 + (-3t)^2). Therefore, our equation for the tangent vector becomes: t(t) = (1/sqrt((1)^2 + (e)^2 + (-3t)^2), e/sqrt((1)^2 + (e)^2 + (-3t)^2), -3t/sqrt((1)^2 + (e)^2 + (-3t)^2)).
Effects of Zero Torsion
If the torsion is zero, it means that the curvature of the curve is constant throughout its length. This means that the curve remains flat and straight, like a line on a plane. This type of curve is known as a planar curve and it has no “twists” or “turns”. Essentially, when the torsion is zero, the curve cannot change direction in any way; it must remain straight and flat.
Understanding the Binormal Plane
A binormal plane is a plane that contains both the tangent line and the normal line at a given point on a curve. The binormal plane is used to describe the curvature of a curve, as it is the locus of all points which have the same rate of change in both the normal and tangent directions. It is also referred to as an osculating plane, which literally means “to kiss” in Latin.
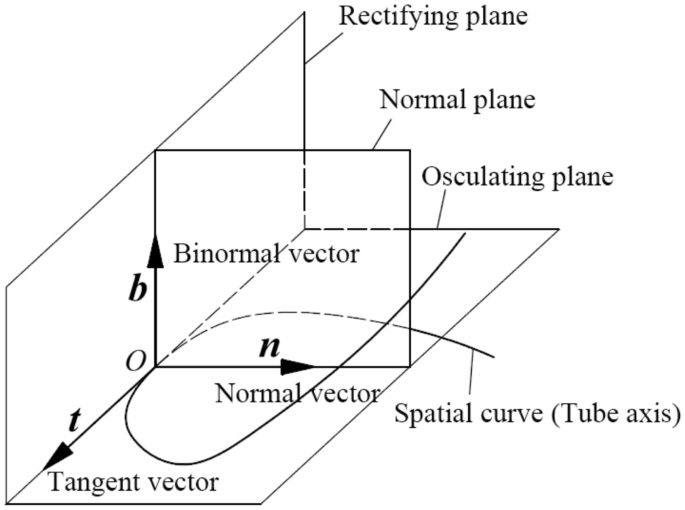
Normal Vector in Differential Geometry
In differential geometry, a normal vector is a vector that is perpendicular to a surface at any given point. This vector can be thought of as the direction in which the surface is most steeply rising. The normal vector can also be used to calculate the curvature of the surface in that particular point. Additionally, the normal vector can be used to define a plane tangent to the surface at that point and it can provide information about line and surface integrals, as well as about local properties of surfaces such as Gaussian curvature.
Understanding the Binomial Theorem in Math
The binomial theorem is a mathematical statement that explains the expansion of the power of a binomial (a polynomial with two terms). Specifically, it states that for any positive integer n, the nth power of the sum of two numbers a and b can be expressed as the sum of n+1 terms of the form. This means that a binomial raised to any power can be written as a sum of various combinations of its two terms. For example, let’s take the expression (x + y)⁴. Using the binomial theorem, this can be written as x⁴ + 4x³y + 6x²y² + 4xy³ + y⁴. As you can see, each term has a coefficient that corresponds to the number of ways in which x and y can be combined to form each particular term in the expression.
Writing a Plane Equation
Writing a plane equation involves finding the components of the normal vector for the plane, which is a vector perpendicular to the plane. The general form of an equation of a plane in ℝ is a ? + ? ? + ? ? + ? = 0, where a, b, and c are the components of the normal vector ⃑n = (a, b, c). To calculate these values, we need two points on the plane and thir respective coordinates. We then subtract one of these points from another to obtain the direction vector for the line formed by these two points. This direction vector gives us some information about the orientation of our plane. We then use this direction vector to calculate the components of our normal vector by taking its cross product with another direction vector that is perpendicular to it. Once we have our normal vector components, we can plug them into our general equation and solve for d to obtain our final equation.
Formula for Analytic Geometry
The formula for analytic geometry is the equation of a line in the two-dimensional plane. This equation, also known as the slope-intercept form, is given by y = mx + b, where m represents the slope of the line and b represents the y-intercept. The slope-intercept form allows us to graph any straight line in an intuitive way and it is one of the most useful tools when dealing with analytic geometry. Additionally, this formula can be used to calculate the distance between two points (x1,y1) and (x2,y2) using the Pythagorean Theorem: d=√[(x2−x1)^2+(y2−y1)^2].
Formulas for Vectors
The formulas for vectors depend on the dimensions of the vector. For a two-dimensional vector, the formula is |a| = √a21+a22. This formula calculates the magnitude (length) of the vector by taking the square root of the sum of squares of its components. For a three-dimensional vector, it is |a| = √a21+a22+a23. This formula calculates the magnitude by taking the square root of the sum of squares of all thre components. Additionally, when working with vectors in higher dimensions (4 or more), you would use the same general formula but with additional terms depending on how many components there are in that particular vector.
What is a Vector Equation?
A vector equation is an equation that involves multiple vectors, which are mathematical objects that have magnitude and direction. Specifically, a vector equation involves a linear combination of vectors with possibly unknown coefficients. In other words, a vector equation can be thought of as asking whether or not a given vector can be expressed as the sum of some other given vectors. Therefore, the answer to this question can be used to determine whether or not the vector equation has a solution.
The Vector Helmholtz Equation
The vector Helmholtz equation is a partial differential equation that describes the behavior of a vector function, f, in relation to its surrounding environment. It is expressed as (Α + k2)f = 0, whre Α is the vector Laplacian and k2 is the square of the wave number. This equation can be used to model a variety of physical phenomena such as sound waves, electromagnetic fields, and light waves. Solutions to this equation often yield insight into how different components interact with each other in various settings. The vector Helmholtz equation is an important tool for understanding the intricate dynamics of our natural world.
Conclusion
In conclusion, the binormal vector is a line that is orthogonal to both the normal vector and the tangent vector of a point on a curve. It forms three orthogonal axes with these two vectors, and can be calculated using a differentiable vector valued function. The binormal vector is used to define the osculating plane, which is an important concept in mathematics and physics.
