Welcome to my blog post about right triangles and the similarities between them! A right triangle is a type of triangle whre one angle is 90 degrees, meaning the other two angles must add up to 90. This type of triangle has many interesting properties, but most importantly, all right triangles are similar.
To understand why all right triangles are similar, it’s important to understand what similarity means. When two figures are similar, they have equal corresponding angles and proportional corresponding lengths. This is known as the Similar Figures Theorem. All right-angled triangles follow this theorem, meaning that they all have equal corresponding angles and proportional corresponding lengths.
Because of this, all right triangles share many properties. For example, the Pythagorean Theorem states that for any right triangle with sides a, b and c (with c being the hypotenuse), a2 + b2 = c2. This theorem works for all right triangles regardless of size or shape because of their similarity.
Right triangles also play an important role in trigonometry. Because of their similarity, trigonometric functions can be used to easily find unknown sides or angles in any given triangle. Trigonometry also allows us to use the properties of sine, cosine and tangent (known as the Sine Rule) to calculate angles and lengths in any right triangle as well.
Finally, it’s important to note that although all right triangles are similar, they can still differ in size and shape depending on their side lengths. For example, an equilateral triangle is a special type of right triangle where all three sides are equal in length; whereas an isosceles triangle is a special type of right triangle where two sides are equal in length while the third side differs from both sides in length.
In conclusion, all right-angled triangles are similar because they follow the Similar Figures Theorem – meaning that they have both equal corresponding angles and proportional corresponding lengths throughout each side of the triangle – making them ideal for use in trigonometry when calculating angles or lengths withn a given triangle.
Are Two Right Triangles Similar?
In order to determine whether or not two right triangles are similar, it is necessary to compare their corresponding sides. If the lengths of the hypotenuse and a leg of one triangle are proportional to the corresponding parts of the other triangle, then the two triangles can be considered similar. Additionally, if all three angles in both triangles are congruent (equal), then they are also similar. By using these criteria, it is possble to determine if two right triangles are similar.
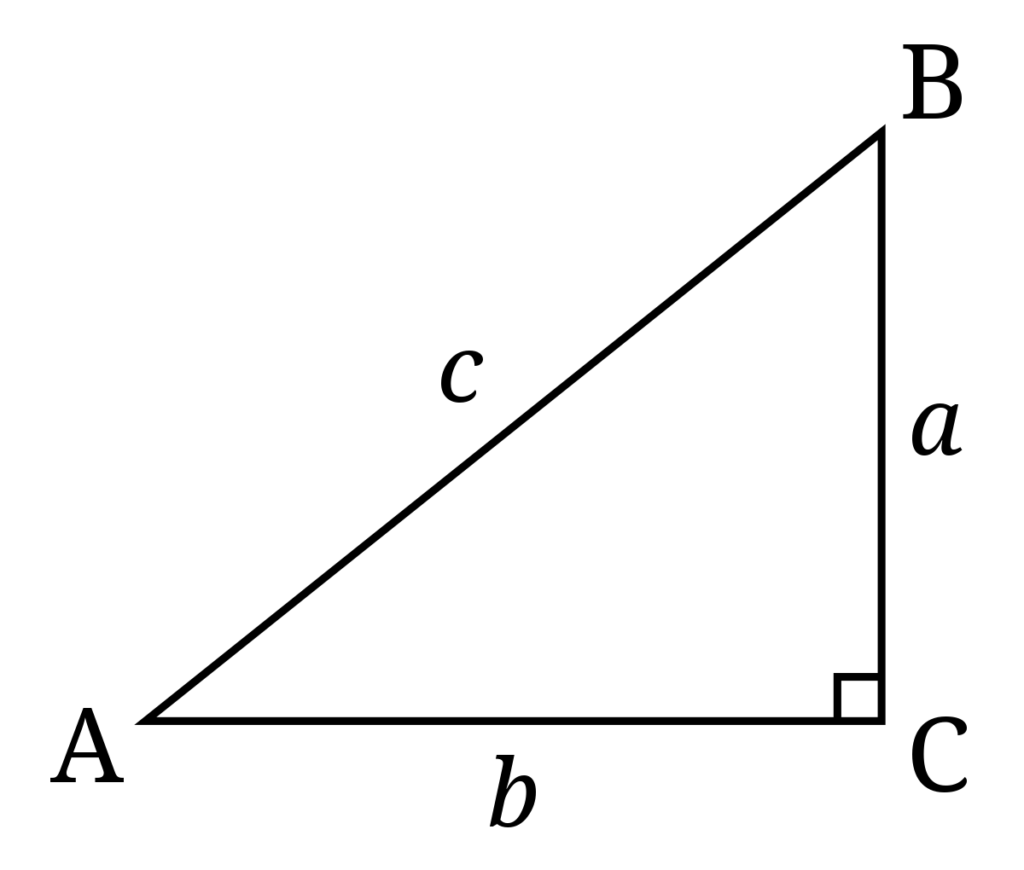
Similarity of Right Triangles
Right triangles are alwys similar because they share a common angle of 90 degrees. This common angle is the same for all right triangles, meaning that their corresponding angles will always be equal. Additionally, the ratio of their side lengths will always be the same, making their corresponding lengths proportional as well. Therefore, all right triangles are similar to one another.
Rules for Proving Two Triangles Are Similar
1. The First Rule of Similarity: The corresponding angles of two triangles are congruent, meaning that their measure is equal. This means that if two triangles have the same angle in one corner, then the other two angles must also be equal.
2. The Second Rule of Similarity: The lengths of the corresponding sides are proportional, meaning that they are all in the same ratio. If a side in one triangle is twice as long as a side in another triangle, then all corresponding sides must have this same ratio.
3. The Third Rule of Similarity: If two triangles satisfy both the First and Second Rules of similarity, then they are similar and any remaining angles or sides will also be proportional or congruent. In other words, if the first two rules are met then all remaining measurements must also fit this pattern to prove similarity.
Proving Similarity of Two Triangles
The three ways to prove that two triangles are similar are Angle-Angle (AA), Side-Angle-Side (SAS), and Side-Side-Side (SSS).
Angle-Angle (AA) states that if two angles of one triangle are equal to two angles of anoher triangle, then the two triangles are similar. For example, if triangle ABC has angle A = angle DEF and angle B = angle EDF, then by AA theorem, triangle ABC is similar to triangle DEF.
Side-Angle-Side (SAS) states that if two sides and the included angle of one triangle are equal to two sides and the included angle of anther triangle, then the two triangles are similar. For example, if triangle ABC has side AB = side DE and angle B = angle E, then by SAS theorem, triangle ABC is similar to triangle DEF.
Finally, Side-Side-Side (SSS) states that if three sides of one triangle are equal to three sides of another triangle, then the two triangles are similar. For example, if triangle ABC has side AB = side DE, side BC = side EF and side AC = side DF then by SSS theorem, triangle ABC is similar to triangle DEF.
By using these thee theorems you can easily determine whether or not two triangles are similar.
Are Right Angles Similar?
No, two right angles are not always similar. Similarity is a relationship between two shapes that preserves the ratio between corresponding sides and angles. Therefore, in order for two shapes to be similar, all of their corresponding sides and angles must have the same ratio. Since two right angles will always have the same angle measure (90°), they can be similar only if they also have the same ratio between their sides. If one right angle has longer sides than the other, then they cannot be similar.
Are Right Angles Always Similar?
No, two rigt angles are not always similar. Similarity is a geometric concept where two shapes have the same shape and size but may be in different positions. Congruence, on the other hand, is a concept where two shapes are the same in both size and position. Two right angles can be congruent but not necessarily similar; they just need to be equal in measure.
Similarity of All Triangles
Equilateral triangles are always similar to each other, meaning all three sides and angles of the triangle are equal. This means that if two equilateral triangles have the same size, they will be exactly the same shape. Additionally, any two equilateral triangles can be made to fit perfectly together because of their equal sides and angles. Furthermore, not only are all equilateral triangles similar to each other, but they are also similar to any other triangle with three equal sides and three equal angles.
Similarity of AAA Triangles
Yes, AAA triangles are similar. This is due to the Angle-Angle-Angle (AAA) theorem, which states that if all three of the corresponding angles of two triangles are equal in measure, then the two triangles are similar. This theorem applies to any type of triangle, including right triangles, obtuse triangles, and acute triangles. Therefore, when all three angles of two diffeent triangles are equal in measure, those two triangles can be considered similar.
Why Some Triangles Are Not Similar
Triangles are not all similar because the angles and the lengths of their sides can vary. All equilateral triangles have three equal angles and three equal side lengths, which makes them all similar. However, other types of triangles have different angles and side lengths, which can make them all different from one another. For example, an isosceles triangle has two equal angles and two equal side lengths, whereas a scalene triangle has no equal sides or angles. Also, an obtuse triangle has one angle that is greater than 90 degrees, which is not present in eiher an isosceles or scalene triangle. Therefore, all triangles are not necessarily similar due to their varying angles and side lengths.
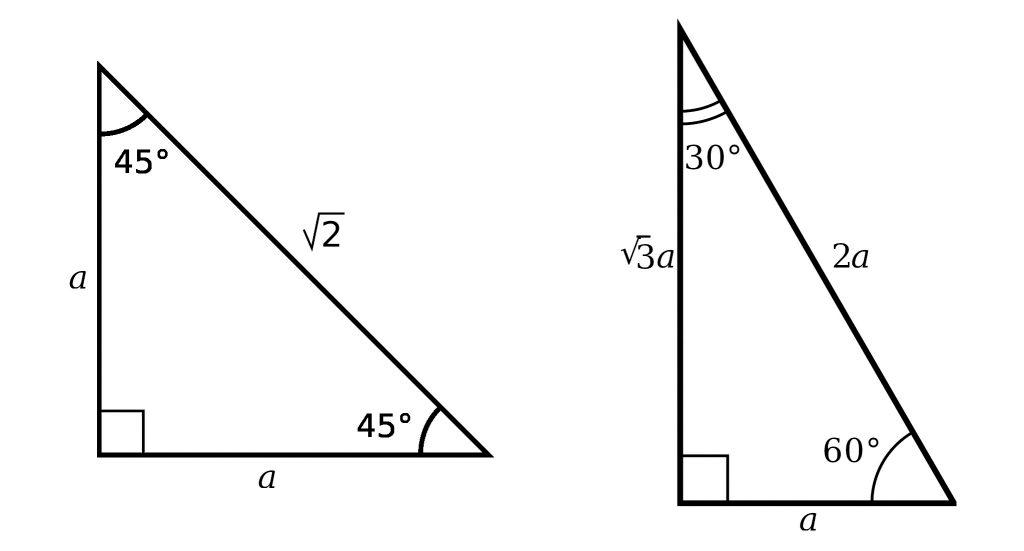
Source: voovers.com
Why Are Some Triangles Not Similar?
Some triangles are not similar because the ratios of the corresonding sides in the triangles are not all the same. In order for two triangles to be similar, they must have three pairs of corresponding sides that have the same ratio. If one or more of those ratios are different, then the triangles will not be similar. Additionally, if we do not know any angle measures for two triangles, then we can use the SSS Similarity Theorem to determine if they are similar. This theorem states that if two triangles have three pairs of corresponding sides that all have the same length, then they must also be similar.
Are Right Triangles Within Right Triangles Similar?
No, a right triangle within a right triangle is not necessarily similar. If the inner right triangle has the same sides as the outer right triangle, then it is similar. However, if the inner right triangle has different sides than the outer right triangle, then it is not similar. For example, if one side of the outer right triangle is twice as long as one side of the inner right triangle, then they are not similar.
Are All Right Triangles Congruent?
No, not all rght triangles are congruent. Two right triangles can have all the same angles but not be congruent. Congruency requires that two shapes are identical in both size and shape, meaning that all corresponding sides and angles must be equal to one another. If all the side lengths of a right triangle are multiplied by the same number, the angles will remain unchanged but the triangles will not be congruent.
Rules for Similar Triangles
The rules for similar triangles are as follows: Two triangles are considered to be similar if they have the same shape but may be different in size. To determine whether two triangles are similar, there are three criteria that must be met.
First, two pairs of corresponding angles must be equal. Second, thee pairs of corresponding sides must be proportional. Third, two pairs of corresponding sides must be proportional and the corresponding angles between them must also be equal.
By meeting thse criteria, it can be determined that two triangles are similar. Furthermore, the ratio between the lengths of their sides will remain consistent for all similar triangles regardless of size or orientation.
Conclusion
In conclusion, right triangles are a special type of triangle with three sides – a hypotenuse and two legs. All right-angled triangles are similar, meaning that ther corresponding angles are equal and their corresponding lengths are proportional. This makes them unique among geometric shapes and is why they are so widely used in mathematics.
