Welcome to our blog post about sides bing congruent! In geometry, the term “congruent” is used to describe two or more objects that are identical in size and shape. Congruency is an important concept when it comes to understanding shapes, angles, and lines.
In essence, congruency of sides means that all sides of a shape have the same length. This is true for squares, rectangles, rhombuses, and parallelograms. For example, a square has four congruent sides that are all equal in length. Similarly, a rectangle has two pairs of congruent sides: the opposite sides are the same length while the other two are different lengths.
A rhombus is like a parallelogram in that it has two pairs of parallel and congruent sides; however, all four of its sides are congruent with each other. The diagonals of a parallelogram also bisect the angles they connect – meaning they divide them into two equal parts – while opposite angles and opposite sides remain congruent as well. Adjacent angles in a parallelogram are supplementary which means they always add up to 180 degrees.
It’s important to note that understanding side congruency helps us understand the properties of shapes better. For instance, if we know that all four sides in a square are congruent then we can make educated guesses about other properties such as its perimeter or area wihout having to measure them out directly.
We hope this blog post was helpful for anyone looking for more information abut side congruency!
Are All Sides of a Rectangle Congruent?
No, not all sides of a rectangle are congruent. In a square, all four sides are congruent and the opposite sides in a rectangle are congruent. However, the other two sides of a rectangle do not have to be the same length or angle measurements as each other.
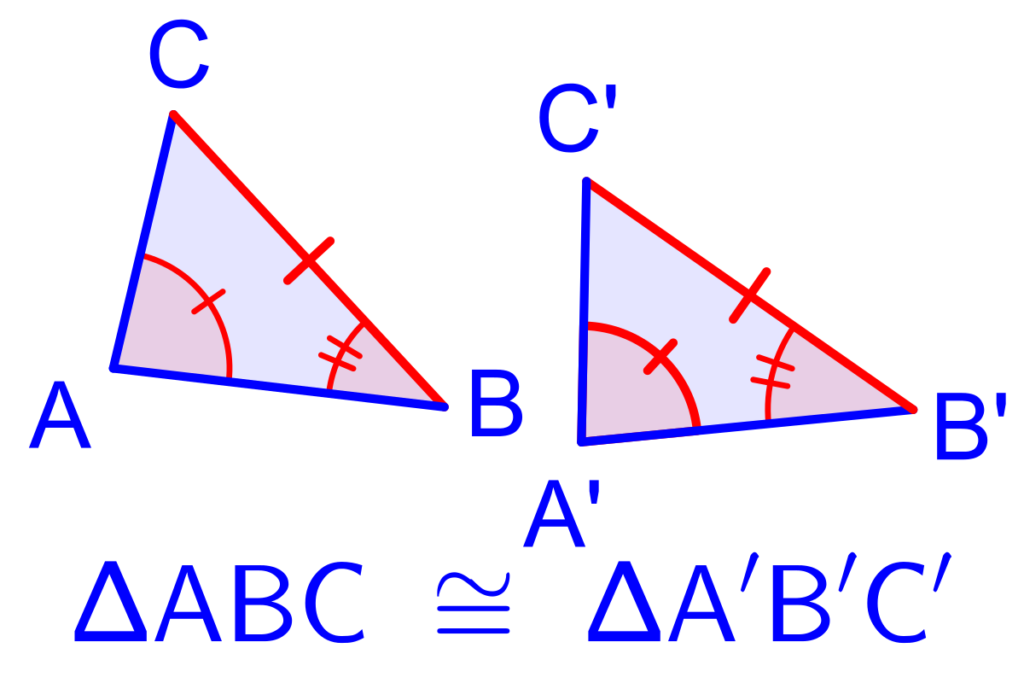
What Does it Mean to Have All Sides Congruent?
All sides congruent means that all the sides of a given shape have the same length. This is an important property of shapes like squares and rectangles, where each side must be equal in length in order for the shape to be considered valid. Congruent sides are also important when comparing shapes, as they allow us to easily determine if two shapes are similar or not.
Are the Sides of a Rhombus Congruent?
Yes, all sides of a rhombus are congruent. This is one of the defining features of a rhombus, and it distinguishes it from other polygons such as parallelograms. The sides of a rhombus are equal in length, and thse sides form angles that are all equal in measure. Furthermore, the diagonals of the rhombus intersect at angles that are exactly half the measure of the angles formed by its sides.
Is a Parallelogram with All Sides Congruent?
No, all sides are not necessarily congruent in a parallelogram. The opposite sides of a parallelogram are parallel and therefore equal in length, but the oter two pairs of sides may differ in length. All four angles of a parallelogram are also equal, however all four sides do not have to be congruent.
Shape with All Congruent Sides
The shape that has all sides congruent is known as a square. A square is a regular quadrilateral, meaning it has four sides of equal length and four angles of equal measure. Its interior angles add up to 360 degrees, and its opposite sides are parallel. It is one of the most recognizable shapes in geometry due to its symmetry and right angles.
Are Trapezoids Congruent on All Sides?
No, all sides are not congruent in a trapezoid. A trapezoid is a four-sided shape with two parallel sides (the bases) and two non-parallel sides (the legs). The angles of a trapezoid do not need to be congruent either, though sometimes the angles might be equal. The diagonals of a trapezoid do not have any special properties, unlike in oter shapes such as rectangles or parallelograms. A special type of trapezoid is an isosceles trapezoid, where the non-parallel legs are both equal in length.
Understanding the Meaning of Congruence
The term “congruent” means that two shapes are exactly equal in both shape and size. This means that the shapes should have the same number of sides and angles, and those sides and angles should be of equal length or degrees. When we flip, turn, or rotate the shapes, they should still remain equal in both shape and size. In other words, no matter how we move them around, the shapes will look identical.
What Does Congruence Mean?
Congruent means to be in agreement or harmony with something. It generally refers to two objects, ideas, or people that share the same characteristics or are otherwise compatible. For example, two triangles might be congruent if they have the same size, shape and orientation. Congruency is an important concept when considering mathematical equations and shapes. It can also be used to describe how two different people or ideas can come together in agreement.
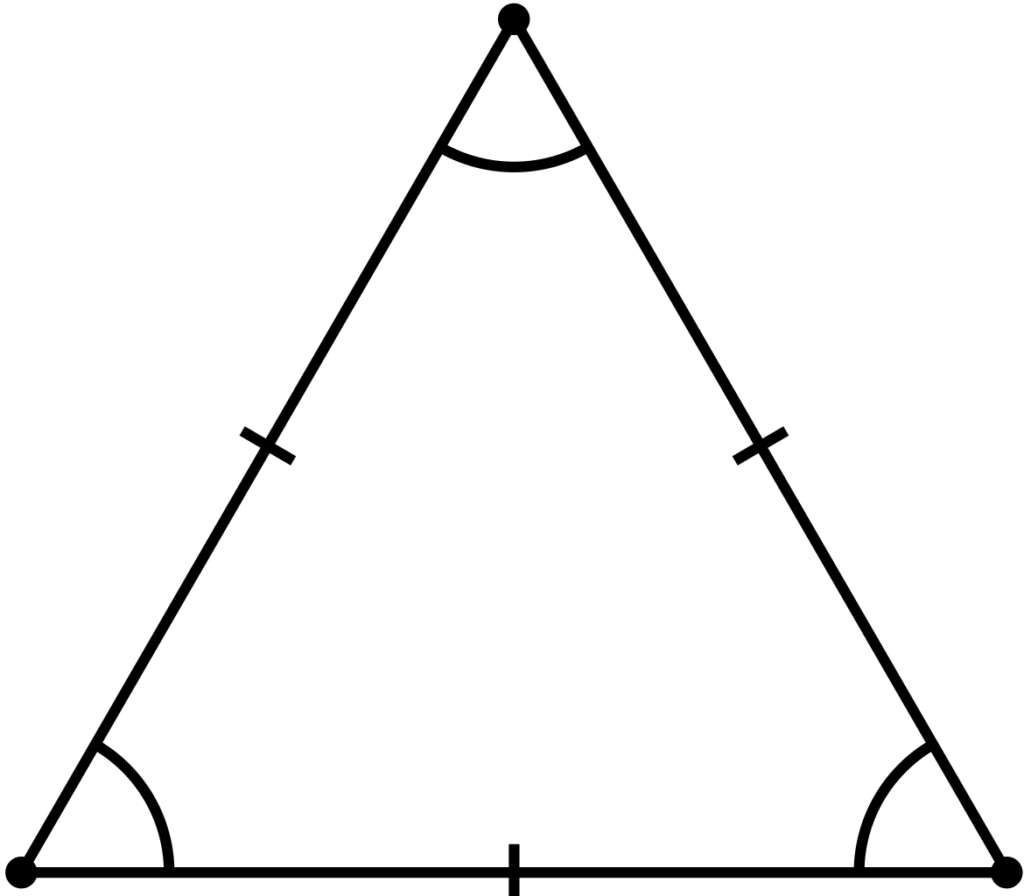
What Type of Triangle Has All Congruent Sides?
An equilateral triangle is a triangle that has all three of its sides congruent, or equal in length. The angles in an equilateral triangle are always 60°. To indicate that all the sides are congruent, you can use a slash mark on each side. Equilateral triangles have a few unique properties – for example, the internal angles of an equilateral triangle always add up to 180° and the perpendicular bisector of any side will also bisect the other two sides.
Are Angles in a Trapezoid Congruent?
No, not all angles in a trapezoid are congruent. However, if a trapezoid is an isosceles trapezoid, then it can be shown that the base angles of the trapezoid are congruent. This is due to the Hypotenuse-Leg Congruence Theorem, which states that if two right triangles share a common hypotenuse, then thir corresponding legs must also be congruent. Since the legs of an isosceles trapezoid are congruent, this means that the base angles of the trapezoid must be congruent as well.
Are Rectangles Congruent?
Yes, a rectangle is congruent. This means that all four of its angles have the same measure and size, and are equal to 90 degrees or a “right angle.” Additionally, opposite sides of the rectangle are parallel to each oter and opposite angles are congruent.
Does a Square Have Congruent Sides?
Yes, a square has four congruent sides. A square is a quadrilateral with four equal length sides and four right angles. This means that the length of all four sides of the square are the same, making them congruent. Additionally, the opposite sides of the square are parallel to each other.
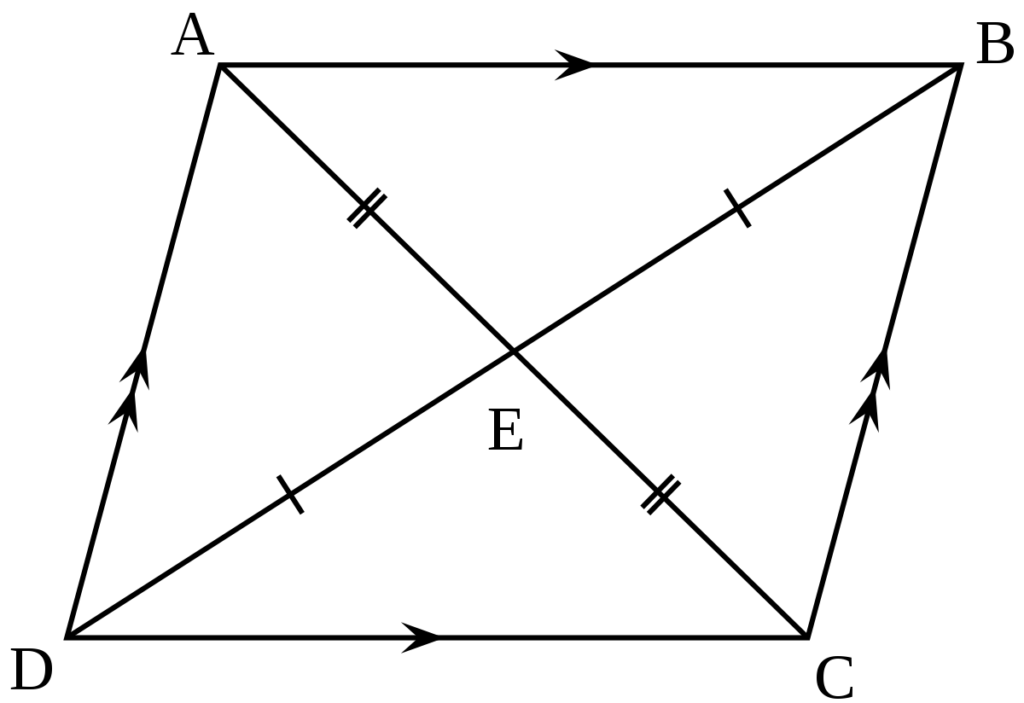
Is a Parallelogram Congruent?
Yes, a parallelogram is congruent. By definition, a parallelogram is a quadrilateral with both pairs of opposite sides parallel. This means that all four angles are of equal measure, making the opposite angles congruent. Additionally, the diagonals of a parallelogram bisect each other, which further demonstrates that the parallelogram is congruent.
Are Angles in a Rectangle Congruent?
Yes, all angles in a rectangle are congruent. A rectangle is a type of parallelogram, which means that its pairs of opposite sides are parallel. In addition to this, a rectangle has the unique property that all four of its angles measure 90 degrees (right angles). This means that the angles in a rectangle are all equal to each other and are therefore congruent.
Which Shapes Have Congruent Sides?
Parallelograms with congruent sides are called rhombuses. A rhombus is a parallelogram with all four sides of equal length, and the opposite angles are equal. The diagonals of a rhombus are perpendicular to each other, and bisect each other at their midpoints. Rhombuses can also be classified as equilateral quadrilaterals since all four sides have the same length.
Conclusion
In conclusion, all four sides of a square are congruent, meaning they have the same length and angles. On the other hand, only the opposite sides of a rectangle are congruent. Furthermore, all sides of a rhombus are congruent and its diagonals bisect the angles that they connect. Lastly, in parallelograms, both opposite sides and opposite angles are congruent whle adjacent angles are supplementary.
