Correlation is a statistical concept that measures the relationship between two variables. When two variables have no relationship, we call it no correlation. A correlation of zero means that the two variables move independently of one another. In this blog post, we will discuss what no correlation means and provide an example to help you better understand the concept.
No correlation is a statistical term used to describe the relationship between two variables. When two variables have no relationship, it means that changes in one variable do not affect the other variable. This means that there is no pattern or trend between the two variables, and they are independent of each other. For example, the number of cars on the road does not affect the number of books sold. These two variables are not related to each other.
An example of no correlation is the relationship between the amount of rainfall and the number of televisions sold. These two variables are not related to each other. An increase in rainfall does not affect the number of televisions sold, and a decrease in rainfall does not affect the number of televisions sold. In this case, there is no pattern or trend between the two variables. They are independent of each other.
No correlation is important to understand becuse it helps us to identify variables that are not related to each other. This means that changes in one variable do not affect the other variable. For example, if we are trying to determine the number of books sold based on the number of cars on the road, we will not get an accurate prediction because these variables are not related to each other.
No correlation is a statistical concept that measures the relationship between two variables. When two variables have no relationship, it means that changes in one variable do not affect the other variable. An example of no correlation is the relationship between the amount of rainfall and the number of televisions sold. Understanding no correlation is important because it helps us to identify variables that are not related to each other.
No Correlation: What Is It?
A no correlation, also known as a zero correlation, refers to a situation where there is no relationship or association between two variables. It means that as one variable increases or decreases, the oter variable does not change in a predictable way. In other words, the two variables are independent of each other and do not influence one another. For instance, the height of a person and their favorite color have no correlation because one does not affect the other. Similarly, the number of hours a student spends studying and their shoe size may have no correlation. A zero correlation is often represented by a correlation coefficient of 0, indicating that there is no linear relationship between the two variables.
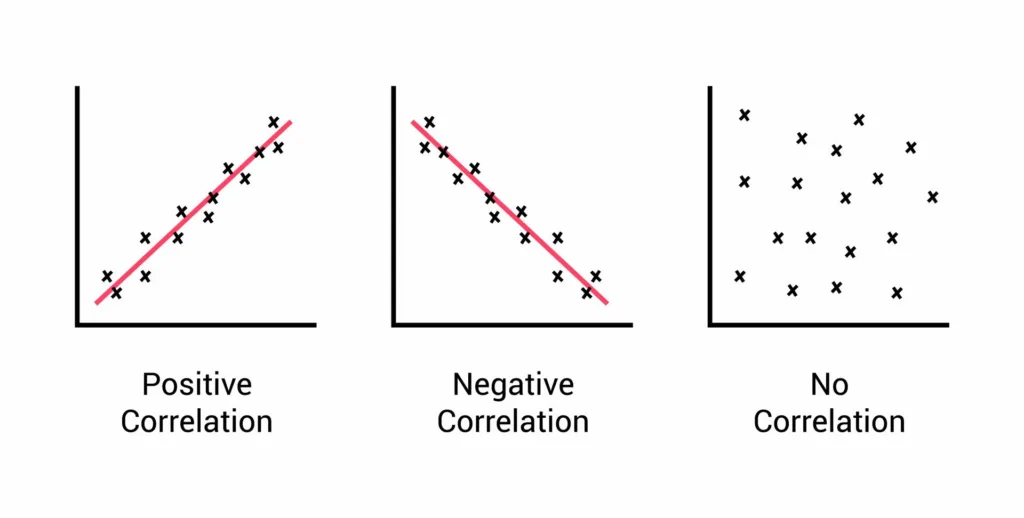
Examples of Correlation
Correlation refers to the statistical relationship between two variables. When two variables tend to change together, they are said to be correlated. There are several examples of correlation in everyday life.
One of the most common examples of correlation is the relationship between height and weight. People who are taller tend to weigh more, and people who are shorter tend to weigh less. This is a positive correlation, meaning that as one variable increases, the other variable also tends to increase.
Another example of correlation is the relationship between temperature and ice cream sales. On hot days, people are more likely to buy ice cream, while on cold days, fewer people buy ice cream. This is also a positive correlation, as temperature and ice cream sales tend to increase together.
Other examples of correlation include the relationship between coffee consumption and intelligence, whee people who drink more coffee tend to score higher on intelligence tests, and the relationship between shoe size and movies watched, where people with larger shoe sizes tend to watch more movies.
Correlation is a statistical relationship between two variables that tend to change together. There are many examples of correlation in our daily lives, including height and weight, temperature and ice cream sales, coffee consumption and intelligence, and shoe size and movies watched.
Shows With No Correlation
In statistics, when we say that two variables have no correlation, we mean that there is no relationship btween them. This implies that the value of one variable does not affect the value of the other variable. Therefore, in terms of TV shows, if we consider two variables such as the genre of the show and the number of seasons, it is possible that these two variables have no correlation. For example, a comedy show can have 10 seasons, but another comedy show can only have one season. Similarly, a drama show can have five seasons, but another drama show can have 15 seasons. In this case, we can conclude that there is no correlation between the genre of the show and the number of seasons. Therefore, it is possible for some TV shows to exhibit no correlation between their different variables.
The Relationship Between 0.2 and Correlation
When we talk abut correlation coefficients, it’s important to understand that the value of the coefficient can range from -1 to 1. A correlation coefficient of 0 means that there is no correlation between the two variables being analyzed, while a correlation coefficient of -1 or 1 represents a perfect negative or positive correlation, respectively.
In the case of a correlation coefficient of 0.2, it indicates that there is a very weak or negligible correlation between the two variables. This means that there is a small relationship between the variables, but it is not significant enough to draw any meaningful conclusions.
Therefore, one can conclude that a correlation coefficient of 0.2 is not considered as no correlation, but rather it represents a weak or negligible correlation.
No Correlation Between Two Variables
When thre is no correlation between two variables, it means that there is no association or relationship between them. In other words, the variables are completely unrelated and there is no pattern or trend that can be observed between them. This is indicated by a simple correlation coefficient of zero, which means that there is no linear relationship between the variables. It is important to note, however, that just because there is no correlation between two variables does not mean that there is no causal relationship or other type of association between them. Additionally, there may be other types of relationships between the variables that are not captured by the simple correlation coefficient, such as non-linear relationships or interactions. Therefore, it is always important to carefully consider the nature of the variables and their potential relationships before drawing any conclusions about their correlation.

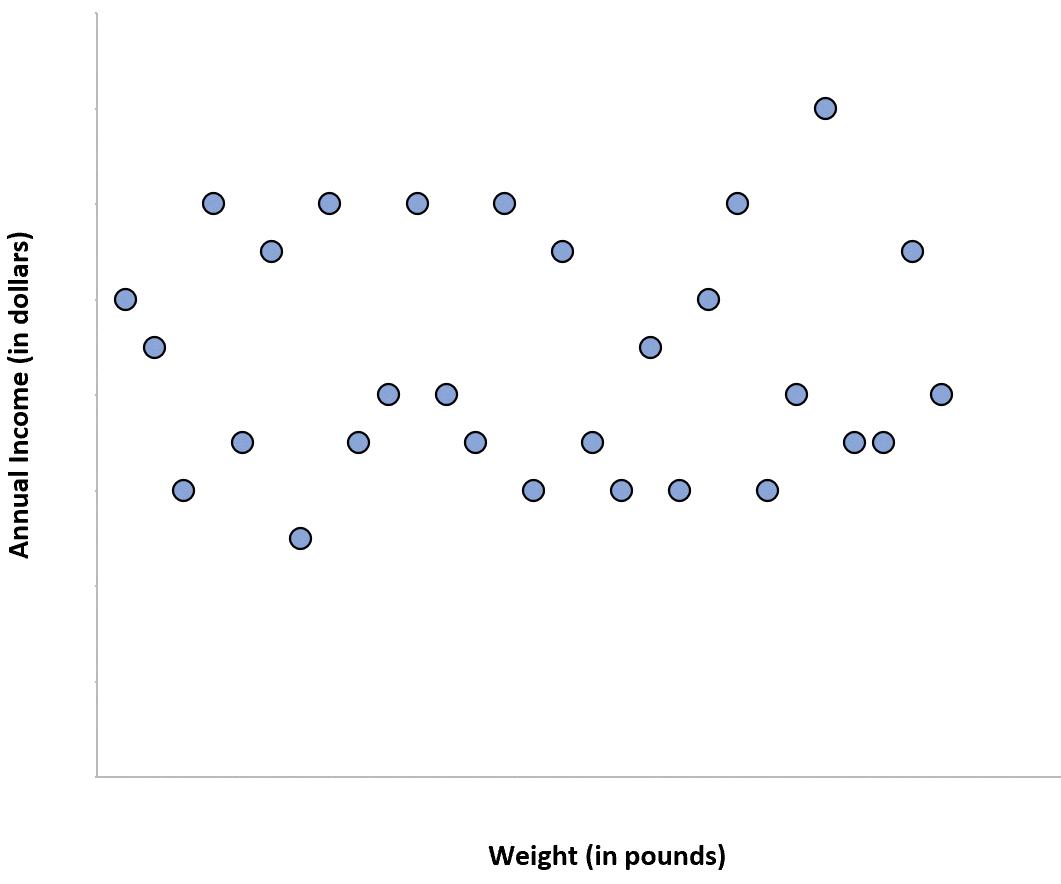
Understanding No Correlation Graphs
A no correlation graph, also known as a scatter plot with no correlation, is a type of graph that displays two variables with no apparent relationship between them. In other words, the variables do not apear to be related in any way, shape, or form. This type of graph is characterized by a scatter of data points that are randomly distributed throughout the graph with no discernible pattern or trend. It is important to note that just because there is no correlation between two variables does not mean that one variable does not affect the other in some way, shape, or form. It simply means that the relationship between the variables is not linear, and there is no way to predict one variable based on the other. A no correlation graph is commonly used in scientific research to determine whether there is a relationship between two variables or not.
Types of Correlation
There are three types of correlation, each representing a different relationship between two variables. The first type is positive linear correlation, which occurs when the value of one variable increases as the value of the other variable increases. The second type is negative linear correlation, which occurs when the value of one variable decreases as the value of the other variable increases. thee is non-linear correlation, which is also known as curvilinear correlation. This type of correlation occurs when there is a relationship between the variables, but it is not a straight line. It can take many forms, such as a curve or a wave-like pattern. It is important to note that there can also be no correlation between variables, meaning there is no relationship between them. Understanding the different types of correlation is crucial in analyzing data and drawing conclusions about the relationship between variables.
Positive and Negative Correlation Examples
Sure! An exmple of a positive correlation is the relationship between exercise and weight loss. As a person increases their level of physical activity, they tend to lose more weight. So, as the amount of exercise increases, so does weight loss. This is a positive correlation because both variables move in the same direction, meaning that when one variable increases, the other variable increases as well.
On the other hand, an example of a negative correlation is the relationship between temperature and heating costs. As the temperature outside decreases, the cost of heating a home tends to increase. So, as the temperature decreases, the heating costs increase. This is a negative correlation because the variables move in opposite directions, meaning that when one variable increases, the other variable decreases.
Examples of Correlational Research
Correlational research is a type of research that examines the relationship between two or more variables. It is used to determine whether there is a correlation or a relationship between variables, but it does not establish a cause-and-effect relationship.
One example of correlational research is a study that examines the relationship between smoking and lung cancer. In this study, researchers would collect data on the smoking habits of a group of people and compare it to the incidence of lung cancer in that same group. The results of this study may show that there is a positive correlation between smoking and lung cancer, which means that people who smoke are more likly to develop lung cancer.
Another example of correlational research is a study that examines the relationship between exercise and mental health. In this study, researchers would collect data on the exercise habits of a group of people and compare it to their mental health status. The results of this study may show that there is a negative correlation between exercise and mental health problems, which means that people who exercise regularly are less likely to experience mental health problems.
Correlational research is a valuable tool for examining relationships between variables and can provide important insights into a wide range of phenomena.
Source: statology.org
Examples of Correlation but Not Causation
An example of correlation but not causation is the relationship between ice cream sales and crime rates. Studies have shown that during the summer months, both ice cream sales and crime rates tend to increase. However, this does not mean that ice cream consumption causes crime. Rather, they are both influenced by a third factor – the warm weather. As the temperature rises, people tend to spend more time outdoors, including criminals, and also tend to consume more ice cream to cool down. Therefore, while ice cream sales and crime rates may be correlated, thee is no evidence to suggest that one causes the other.
Examples of Negative Correlation in Real Life
Sure, I’d be happy to provide you with a detailed answer. Negative correlation is a statistical term that describes a relationship between two variables where one variable increases as the other variable decreases. A real-life example of negative correlation can be seen in the relationship between the number of hours a student spends playing video games and their academic performance. As the number of hours spent playing video games increases, their academic performance tends to decrease. This is because the time spent playing video games takes away from time that culd be spent studying or completing homework. Another example could be the relationship between the amount of exercise someone gets and their body weight. As someone exercises more, their body weight tends to decrease due to burning calories and building muscle. So, these are some of the common examples of negative correlation that we can observe in our daily lives.
Determining the Absence of Correlation in a Graph
When we look at a graph, we can tell if there is no correlation between the two variables when there is no clear pattern or trend in the data. In other words, there is no relationship between the values of the x variable and the values of the y variable. This is indicated by scattered data points that do not follow a paticular direction or trend.
To confirm that there is no correlation, we can also calculate the correlation coefficient, which is a statistical measure of the strength and direction of the relationship between two variables. If the correlation coefficient is close to 0, then there is no correlation between the variables. Additionally, we can perform a hypothesis test to determine if the correlation coefficient is significantly different from 0, which would indicate a non-zero correlation.
A graph with no correlation will have scattered data points with no clear pattern or trend, and the correlation coefficient will be close to 0.
The Relationship Between 0.03 and Correlation
Actually, a p-value of 0.03 indicates that there is a statistically significant correlation between the two variables being analyzed. Typically, a p-value less than or equal to the predetermined alpha level (usually 0.05) is considered statistically significant, meaning that the likelihood of observing such a correlation by chance alone is less than 5%. Therefore, we can conclude that there is inded a correlation present, and it may be worth further investigating the strength and direction of this correlation. It is important to note that the magnitude of the correlation should also be taken into account, as a statistically significant correlation does not necessarily mean that it is practically significant or meaningful in real-world terms.
The Strength of a 0.45 Correlation
0.45 is generally considered a weak correlation. Correlation coefficients range from -1 to 1, with values closer to -1 or 1 indicating a stronger relationship between two variables. When the correlation coefficient is closer to 0, it indicates a weaker relationship or no relationship at all. Therefore, a correlation coefficient of 0.45 is on the weaker end of the spectrum and suggests only a moderate positive relationship between the two variables being studied. It is important to note that the interpretation of a correlation coefficient may vary depending on the context and the field of study.
The Relationship Between No Correlation and Zero
No correlation is represented by a correlation coefficient of 0. When two variables have no relationship, their correlation coefficient will be close to 0. This means that there is no linear relationship between the two variables. It’s important to note that a correlation coefficient of 0 does not necessarily mean that there is no relationship between the two variables at all, just that there is no linear relationship. Other types of relationships, such as a curvilinear relationship, may still exist.
Conclusion
When two variables show no correlation, it means that they are not related to one another. This lack of relationship can be represented by a correlation coefficient of 0, which indicates that as one variable changes, the other does not change in any predictable way. This can be seen in various examples, such as height vs weight, temperature vs ice cream sales, or coffee consumption vs intelligence. It is important to note that a correlation coefficient of 0 does not necessarily mean that there is no causal relationship btween the variables, but rather that there is no linear relationship between them. Therefore, when analyzing data, it is crucial to consider the correlation coefficient and its implications in order to draw accurate conclusions.
