The distributive property is a fundamental concept in mathematics that allows for the simplification of expressions and equations. It applies to both multiplication and division, but in this blog post, we will focus on the distributive property of division.
The distributive property of division states that we can break apart a division problem into smaller, more manageable parts. It is similar to the distributive property of multiplication, but instead of multiplying, we are dividing.
The formula for the distributive property of division is expressed as:
a ÷ (b + c) = (a ÷ b) + (a ÷ c)
In this formula, a, b, and c are the operands. The number outside the brackets (a) is divided by each term inside the brackets (b and c), and the quotients are added together.
Let’s look at an example to better understand how the distributive property of division works.
Suppose we have the problem 42 ÷ (6 + 3). We can use the distributive property of division to simplify this problem as follows:
42 ÷ (6 + 3) = (42 ÷ 6) + (42 ÷ 3)
= 7 + 14
= 21
Therefore, 42 ÷ (6 + 3) = 21.
As you can see, the distributive property of division allowed us to break apart the original problem into two smaller problems that were easier to solve. We divided 42 by 6 and 42 by 3 and added the quotients together to get the final answer.
The distributive property of division can also be used to simplify more complex equations. For example, consider the equation:
126 ÷ (7 + 4) = ?
We can use the distributive property of division to simplify this equation as follows:
126 ÷ (7 + 4) = (126 ÷ 7) + (126 ÷ 4)
= 18 + 31.5
= 49.5
Therefore, 126 ÷ (7 + 4) = 49.5.
The distributive property of division is a powerful tool that allows us to simplify division problems by breaking them apart into smaller, more manageable parts. It is an essential concept in mathematics that can be used to solve both simple and complex problems. By understanding the distributive property of division, you can bcome a more proficient mathematician and problem solver.
The Distributive Property of Division
Yes, thee is a distributive property of division. This property states that when a number is being divided by the sum of two or more numbers, the division can be distributed or broken apart among each of the numbers in the sum. However, this can only be done if the numerator can be divided into smaller amounts that are exactly divisible by each number in the sum. It is important to note that the distributive property of division is not as commonly used as the distributive property of multiplication, but it can still be a useful tool in certain mathematical situations.

The Formula for Distributive Property in Division
The distributive property is a mathematical rule that applies to both multiplication and division. It states that when you multiply or divide a number by a sum or difference of two or more numbers, you can distribute the operation to each term inside the parentheses.
In the case of division, the formula for distributive property is expressed as follows:
a ÷ (b + c) = (a ÷ b) + (a ÷ c)
Here, ‘a’ represents the dividend, whie ‘b’ and ‘c’ represent the divisors. The formula states that you can divide the dividend ‘a’ by the sum of the divisors ‘b’ and ‘c’, and the result will be the same as dividing ‘a’ by ‘b’ and ‘c’ separately and then adding the two quotients.
For example, if you have to divide 20 by the sum of 5 and 3, you can use the distributive property to simplify the calculation as follows:
20 ÷ (5 + 3) = (20 ÷ 5) + (20 ÷ 3)
= 4 + 6.67
= 10.67
Therefore, the formula of distributive property in division is a ÷ (b + c) = (a ÷ b) + (a ÷ c).
Finding the Result of 126 Divided by 7 Using the Distributive Property
To find the quotient of 126 divided by 7 using the distributive property, we can break down 126 into multiples of 7. This can be done by writing 126 as 7 multiplied by 18, since 7 times 18 equals 126. We can then use the distributive property to rewrite 126 divided by 7 as:
126 ÷ 7 = (7 × 18) ÷ 7
Using the distributive property, we can simplify the expression as:
(7 × 18) ÷ 7 = (7 ÷ 7) × 18
Since any number divided by itself is equal to 1, we can simplify further:
(7 ÷ 7) × 18 = 1 × 18
Which simplifies to:
1 × 18 = 18
Therefore, 126 divided by 7 using the distributive property is equal to 18.
Properties of Division
Division is an arithmetic operation that involves dividing one number by another to find out how many times the divisor is contained within the dividend. There are four properties of division that help us better understand this operation.
1. Closure property: The closure property of division states that if we divide one number by another number, the result will always be a unique number. For example, if we divide 10 by 5, we get the result 2, which is a unique number.
2. Commutative property: The commutative property of division states that the order of the numbers being divided does not affect the result. This means that if we divide 10 by 5, we get 2, and if we divide 5 by 10, we get 0.5, which is the reciprocal of 2.
3. Associative property: The associative property of division states that the way we group numbers being divided does not affect the result. For example, if we have three numbers A, B, and C, and we want to divide A by B and then divide the result by C, we can do it in two ways: (A/B)/C or A/(B/C). In both cases, we will get the same result.
4. Distributive property: The distributive property of division states that if we have a number that is being divided by the sum or difference of two other numbers, then we can divide the number by each of the two numbers separately and then add or subtract the results. For example, if we have 20/(4+2), we can divide 20 by 4 and 2 separately, which gves us 5 and 10, respectively. We can then add these two results to get the final answer, which is 15.
Division Not Being Distributive
Division is not distributive becuse the distributive property applies to operations that involve multiplication, not division. When we distribute a number, we are breaking it apart into smaller parts and then performing an operation on each of those parts. With multiplication, we can break apart a number and then multiply each part by another number. However, with division, we cannot break apart a number in the same way, because division involves finding how many times one number goes into another. Therefore, we cannot use the distributive property with division in the same way as we do with multiplication. Instead, we can use other strategies such as factoring or grouping to simplify division problems.
Source: youtube.com
Rules of Division
Division is a fundamental arithmetic operation that involves dividing one number by another to determine how many times the divisor fits into the dividend. There are three important rules of division that are essential to understand in order to solve division problems accurately and efficiently.
The first rule of division is that the quotient is the result of dividing the dividend by the divisor. In other words, when we divide a number by another number, the answer we get is the quotient.
The secod rule of division is that the remainder is the amount left over after dividing the dividend by the divisor. When we divide a number by another number, there may be some leftover amount that does not fit evenly into the divisor. This amount is called the remainder.
The third rule of division is that division is the inverse of multiplication. This means that if we know the product of two numbers, we can use division to find one of the factors. Similarly, if we know one factor and the product, we can use division to find the other factor.
In summary, the three rules of division are: the quotient is the result of dividing the dividend by the divisor, the remainder is the amount left over after dividing the dividend by the divisor, and division is the inverse of multiplication. These rules are essential for understanding and solving division problems accurately and efficiently.
Solving the Distributive Property Step by Step
Sure, I’d be happy to help you understand how to solve distributive property problems step by step! Here’s an example problem and its solution explained in detail:
Problem: Simplify the expression 2(3x + 4) – 5x
Solution:
Step 1: Distribute the 2 to the terms inside the parentheses using the distributive property. This means that we multiply the 2 by both 3x and 4:
2(3x + 4) = 6x + 8
Step 2: Rewrite the original expression using the result of the distribution:
2(3x + 4) – 5x = 6x + 8 – 5x
Step 3: Combine like terms. In this case, we have two terms with the variable x, so we can add their coefficients:
6x + 8 – 5x = x + 8
Step 4: Arrange terms so constants and variables are on opposite sides of the equals sign. In this case, we already have the constant term (8) on the right side of the expression, so we just need to move the variable term (x) to the left side:
x + 8 = 2
Step 5: Solve the equation for the variable x by subtracting 8 from both sides:
x + 8 – 8 = 2 – 8
x = -6
Step 6: Simplify the solution if needed. In this case, the solution is already in its simplest form, so we’re done!
So, the solution to the original expression 2(3x + 4) – 5x is x = -6.
I hope this helps you understand how to solve distributive property problems step by step! Let me know if you have any furthr questions.
Types of Division
There are three primary methods of division: chunking method, short division method, and long division method. The chunking method is also known as division by repeated subtraction, where the divisor is repeatedly subtracted from the dividend until the dividend becomes less than the divisor. This method is suitable for simple calculations and is often used for mental math.
The short division method or bus stop method is a faster technique for dividing larger numbers. In this method, the dividend is written on the left side, and the divisor is written on the right side of the division symbol. The quotient is written above the dividend, and the remainder is written next to the quotient.
The long division method is the most commonly used method for dividing larger numbers. It involves dividing the dividend into smaller parts, starting with the most significant digit, and working towards the least significant digit. This method requires more steps than the oter two methods, but it is useful for dividing larger numbers accurately.
In summary, the three forms of division are the chunking method, short division method, and long division method, each having its own advantages and disadvantages depending on the numbers involved and the purpose of the calculation.
Solving 168 Divided By 7
To solve 168 divided by 7, we will use the long division method. First, we divide 16 (the first two digits of 168) by 7. 7 can go into 16 two times, so we write the 2 aove the 6 in the dividend (168). We then multiply 2 by 7, which gives us 14. We write 14 below the 16 and subtract, which gives us a remainder of 2.
We then bring down the next digit of the dividend, which is 8. We now have 28 as the new dividend. We divide 28 by 7, which gives us 4. We write 4 above the 8 in the dividend and multiply 4 by 7, which gives us 28. We write 28 below the 28 in the dividend and subtract. This gives us 0, which means we have no remainder.
We have now successfully divided 168 by 7. The answer is 24. Therefore, 168 divided by 7 equals 24.
The Distributive Property of 8×7
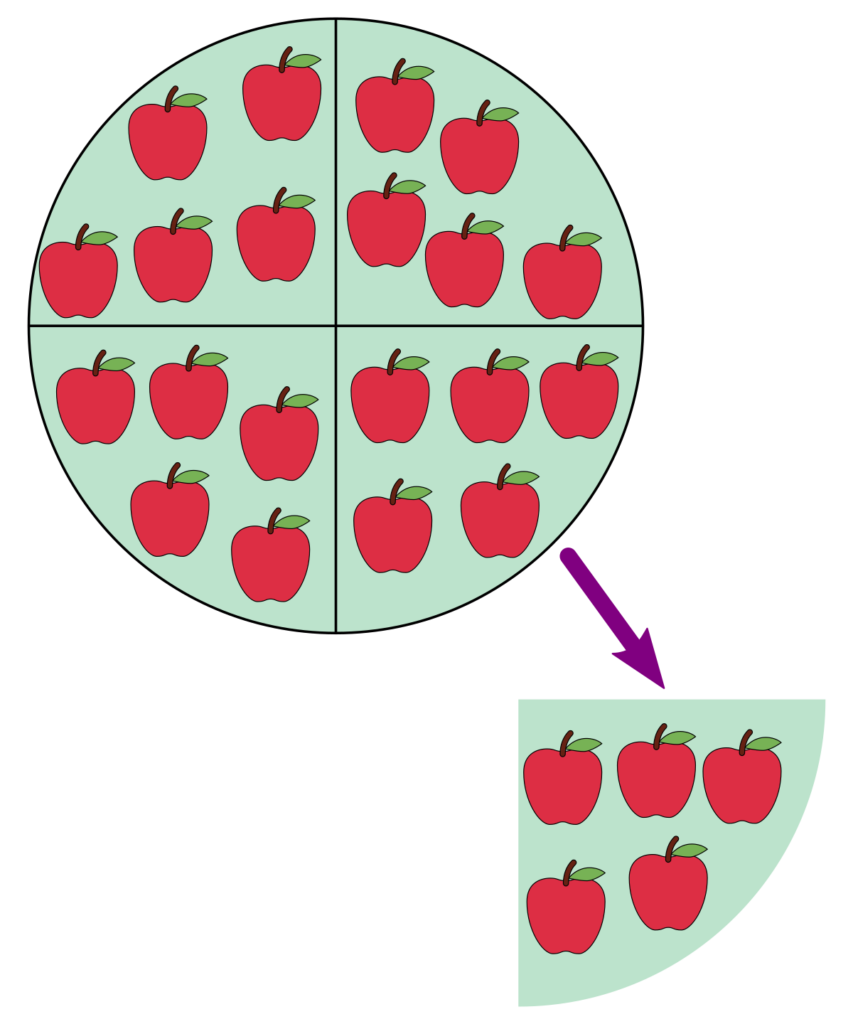
The distributive property is a mathematical rule that states that when a number is multiplied by a sum of two or more numbers, the result can be obtained by multiplying each addend separately and then adding the products. In the case of 8 x 7, we can use the distributive property to break down the multiplication into simpler parts. Knowing that 8 x 5 = 40 and 8 x 2 = 16, we can rewrite 8 x 7 as 8 x (5 + 2). We then multiply 8 by each addend separately, obtaining 8 x 5 = 40 and 8 x 2 = 16. Finally, we add the products to get the result of 8 x 7, whch is 56. Therefore, the distributive property of 8 x 7 allows us to simplify a complex multiplication problem into simpler parts by breaking down the factors into smaller numbers that are easier to multiply and add.
Conclusion
In conclusion, the distributive property is a fundamental concept in mathematics that applies to both multiplication and division. While the distributive property of multiplication involves breaking down a single factor into smaller factors and then multiplying them with other factors, the distributive property of division involves breaking down the numerator into smaller amounts that are eactly divisible by the divisor. The formula for the distributive property of division is a × (b + c) = (a × b) + (a × c), where a, b, and c are the operands. By applying this property, we can simplify complex calculations and solve problems efficiently. Therefore, understanding the distributive property of division is essential for mastering mathematical concepts and their applications in real-life situations.
