Matrices are powerful mathematical tools that can be used to solve complex problems. But one of the most common questions about matrices is, “Can you add matrices with different dimensions?” The answer to this question is no, you cannot add or subtract matrices with different dimensions.
When adding or subtracting matrices, the size of the two matrices must be the same. For example, a 3×2 matrix cannot be added to a 2×2 matrix because they are not the same size. The same rule applies when solving equations with matrices – if the two matrices do not have the same size and shape, then they cannot be added or subtracted.
In order to add two matrices together, they must first have the same size and shape. Once two compatible matrices are found, we can proceed with adding them together. The process is simply adding each corresponding element of each matrix together and putting the result into a new matrix. So for instance, if we had a 3×2 matrix A and a 3×2 matrix B, we would add each of thir elements together like so:
A[1][1] + B[1][1], A[1][2] + B[1][2], A[2][1] + B[2][1], A[2][2] + B[2][2], etc…
This would give us our resulting 3×2 matrix C which contains all of our summed elements from our original two matrices.
The same process can be used for subtracting two compatible matrices as well – simply subtract each element of one matrix from its corresponding element in the other. This will give us our resulting matrix that contains all of our subtracted elements from our original two compatible matrices.
Finally, it’s important to note that unlike addition and subtraction operations between compatible matrices, multiplication operations between incompatible ones is not possible in general. In order to multiply two matrices together, they must have compatible dimensions – meaning that there must be an equal number of columns in the first matrix as there are rows in the second one (i.e., an mxn multiplied by an nxp will result in an mxp). If these conditions are not met then multiplication is impossible between those two particular incompatible matrices.
Overall, it’s important to remember that adding and subtracting between incompatible sized/shaped matrices is impossible but multiplying them can still be done under certain conditions (i.e., compatible dimensions). We hope this article has helped clarify some confusion about how different types of operations work on different types of compatible/incompatible sized/shaped matricies!
Adding Matrices with Different Dimensions
Yes, in order to add or subtract matrices, they must have the same dimensions. This means that both matrices must have the same number of rows and columns. For example, a 3×2 matrix CANNOT be added to a 2×2 matrix because they do not have the same size. Similarly, a 3×3 matrix can only be added to another 3×3 matrix. In other words, both matrices must have the exact same dimensions in order to be added together.

Adding a 2×3 and a 3×2 Matrix
No, you cannot add a 2×3 matrix and a 3×2 matrix because they are not of the same shape/size/dimension. In order to add two matrices, they must have the same number of rows and columns. A 2×3 matrix has two rows and three columns, while a 3×2 matrix has three rows and two columns. Therefore, these matrices cannot be added together because their dimensions are not equal.
Can Matrices of Different Dimensions Be Added Together?
No, all matrices cannot be added together regardless of their dimensions. In order to add two matrices together, they must have the same number of rows and columns. If the two matrices do not have the same dimensions, then we cannot add them together and instead must use matrix operations such as multiplication or division to combine them.
Can Matrices of Different Dimensions Be Multiplied?
No, you cannot multiply matrices with different dimensions. The two matrices must have the same number of columns in the first matrix as the number of rows in the second matrix for multiplication to be possible. If the dimensions are not compatible, then it is not possible to perform multiplication between them.
Adding 1×2 and 2×1 Matrices
No, you cannot add a 1×2 and a 2×1 matrix because the two matrices do not have the same dimensions. In order to add two matrices, they must be the same size. A 1×2 matrix has two columns and one row, while a 2×1 matrix has one column and two rows. Since these two matrices do not have the same number of columns or rows, they cannot be added together.
Adding Different Dimensions to a Project
No, we cannot add two different dimensions. This is because adding two quantities requires that they have the same dimensions or units, so that the result will also have the same dimensions or units. For example, if you wanted to add two lengths, you would need to make sure they were both in the same unit of measurement, such as meters or feet. If one length was measured in meters and the other was measured in feet, then adding them together wouldn’t make sense because the result would be a meaningless combination of meters and feet. Similarly, when attempting to add two quantities with different dimensions, such as mass and speed, it wouldn’t be possile because the result would be a meaningless combination of mass and speed.
Adding a 3×2 and a 2×4 Matrix
No, you cannot add a 3×2 matrix and a 2×4 matrix because they are not of the same size. In order to add matrices, both matrices must be of the same size, with the same number of rows and columns. In this case, the 3×2 matrix has three rows and two columns, while the 2×4 matrix has two rows and four columns. Since these two matrices do not have the same number of rows or columns, they cannot be added together.
Adding 3×3 Matrices
Yes, you can add 3×3 and 3×3 matrices. To do so, you need to make sure that both matrices have the same order (meaning they must both be 3×3). Once you have confirmed that the order of the two matrices is the same, you can add them together by matching up each element in one matrix with its corresponing element in the other matrix. When you match up each pair of elements in the two matrices, simply add them together to get their sum. Finally, once all elements in both matrices are added together, your result will be a new matrix with the same order as the two original matrices.
Necessary Condition for Adding Matrices
In order for two matrices to be added together, they must have the same dimensions. This means that both matrices must have the same number of rows and columns. If one matrix has more rows or columns than the other, it is not possible to add them together. Additionally, it is important to make sure that each element in both matrices corresponds to one another in terms of the row and column they are located in. If these conditions are met, then two matrices can be added together by simply adding the numerical values of each corresponding element together.
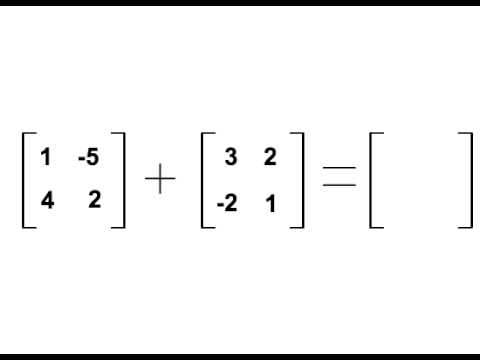
What Causes Undefined Matrix Addition?
A matrix is made up of a set of numbers arranged in rows and columns. When two matrices are added, the resulting matrix should have the same size as the two matrices beng added. If the two matrices don’t have the same size, then it is impossible to add them together because there won’t be any corresponding entries in each matrix that can be added together. In other words, it would be like trying to add two apples to three oranges – it just doesn’t make logical sense! Therefore, when attempting to add two matrices that are not of the same size, the result is undefined.
Adding Matrices of Different Dimensions
Adding two matrices of different dimensions is not possible, as the addition of two matrices requires them to have the same dimensions. In other words, for two matrices to be added together, they must have the same number of rows and columns. If the matrices have different dimensions, then they cannot be added together.
Multiplying a 4×3 and a 2×3 Matrix
No, you cannot multiply a 4×3 and a 2×3 matrix together. For two matrices to be multiplicable, the number of columns in the first matrix must be equal to the number of rows in the second matrix. In this case, the first matrix has 4 columns and the second has 3 rows, which do not match. Therefore, this product is undefined.
Multiplying 3×2 and 3×2 Matrices
Yes, you can multiply a 3×2 and a 3×2 matrix. In order to do so, the number of columns in the first matrix must be equal to the number of rows in the second matrix. In this case, both matrices have three columns and two rows, meaning that they can be multiplied together. The result of multiplying these two matrices will be a 3×2 matrix containing the product of each pair of corresponding entries from the two original matrices.
Conclusion
In conclusion, matrices are used to represent data in a compact and organized way. Matrices can be added, subtracted, and multiplied together as long as their dimensions are compatible. This allows for quickly solving complex equations and representing large amounts of data with ease. Additionally, matrices can be used to solve linear equations and perform other operations such as matrix inversion and determinant calculation. With matrices, we can quickly analyze data in a concise manner and make accurate decisions.
